fitrqlinear

Train quantile linear regression model

Since R2024b

collapse all in page

Syntax

Mdl = fitrqlinear(Tbl,ResponseVarName)

Mdl = fitrqlinear(Tbl,formula)

Mdl = fitrqlinear(Tbl,Y)

Mdl = fitrqlinear(X,Y)

Mdl = fitrqlinear(___,Name=Value)

Description

Mdl = fitrqlinear(Tbl,ResponseVarName) returns a trained quantile linear regression model Mdl. The function trains the model using the predictors in the table Tbl and the response values in the ResponseVarName table variable.

By default, the function uses the median (0.5 quantile).

Mdl = fitrqlinear(Tbl,formula) returns a quantile linear regression model trained using the sample data in the table Tbl. The input argument formula is an explanatory model of the response and a subset of the predictor variables in Tbl used to fit Mdl.

Mdl = fitrqlinear(Tbl,Y) returns a quantile linear regression model trained using the predictor variables in the table Tbl and the response values in the vector Y.

Mdl = fitrqlinear(X,Y) returns a quantile linear regression model trained using the predictors in the matrix X and the response values in the vector Y.

Mdl = fitrqlinear(___,Name=Value) specifies options using one or more name-value arguments in addition to any of the input argument combinations in previous syntaxes. For example, you can specify the quantiles by using the Quantiles name-value argument.

example

Examples

collapse all

Fit Quantile Linear Regression Model

Open Live Script

Fit a quantile linear regression model using the 0.25, 0.50, and 0.75 quantiles.

Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a matrix X containing the predictor variables Acceleration, Displacement, Horsepower, and Weight. Store the response variable MPG in the variable Y.

load carbig
X = [Acceleration,Displacement,Horsepower,Weight];
Y = MPG;

Delete rows of X and Y where either array has missing values.

R = rmmissing([X Y]);
X = R(:,1:end-1);
Y = R(:,end);

Partition the data into training data (XTrain and YTrain) and test data (XTest and YTest). Reserve approximately 20% of the observations for testing, and use the rest of the observations for training.

rng(0,"twister") % For reproducibility of the partition
c = cvpartition(length(Y),"Holdout",0.20);

trainingIdx = training(c);
XTrain = X(trainingIdx,:);
YTrain = Y(trainingIdx);

testIdx = test(c);
XTest = X(testIdx,:);
YTest = Y(testIdx);

Train a quantile linear regression model. Specify to use the 0.25, 0.50, and 0.75 quantiles (that is, the lower quartile, median, and upper quartile). To improve the model fit, change the beta tolerance to 1e-6 instead of the default value 1e-4. Use a ridge (L2) regularization term of 1. Adding a regularization term can help prevent quantile crossing.

Mdl = fitrqlinear(XTrain,YTrain,Quantiles=[0.25,0.50,0.75], ...
    BetaTolerance=1e-6,Lambda=1)

Mdl = 
  RegressionQuantileLinear
             ResponseName: 'Y'
    CategoricalPredictors: []
        ResponseTransform: 'none'
                     Beta: [4x3 double]
                     Bias: [17.0004 23.0029 29.5243]
                Quantiles: [0.2500 0.5000 0.7500]

Mdl is a RegressionQuantileLinear model object. You can use dot notation to access the properties of Mdl. For example, Mdl.Beta and Mdl.Bias contain the linear coefficient estimates and estimated bias terms, respectively. Each column of Mdl.Beta corresponds to one quantile, as does each element of Mdl.Bias.

In this example, you can use the linear coefficient estimates and estimated bias terms directly to predict the test set responses for each of the three quantiles in Mdl.Quantiles. In general, you can use the predict object function to make quantile predictions.

predictedY = XTest*Mdl.Beta + Mdl.Bias

predictedY = 78×3

   12.3963   16.2569   19.5263
    5.8328   10.1568   12.6058
   17.1726   20.6398   24.9748
   23.3790   28.1122   31.3617
   17.0036   22.5314   23.0539
   16.6120   17.0713   20.1062
   10.9274   12.3302   13.2707
   14.9130   14.6659   12.7100
   16.3103   17.7497   20.8477
   19.6229   25.7109   30.5389
      ⋮

isequal(predictedY,predict(Mdl,XTest))

ans = logical
   1

Each column of predictedY corresponds to a separate quantile (0.25, 0.5, or 0.75).

Visualize the predictions of the quantile linear regression model. First, create a grid of predictor values.

minX = floor(min(X))

minX = 1×4

           8          68          46        1613

maxX = ceil(max(X))

maxX = 1×4

          25         455         230        5140

gridX = zeros(100,size(X,2));
for p = 1:size(X,2)
    gridp = linspace(minX(p),maxX(p))';
    gridX(:,p) = gridp;
end

Next, use the trained model Mdl to predict the response values for the grid of predictor values.

gridY = predict(Mdl,gridX)

gridY = 100×3

   20.8073   25.4104   29.1436
   20.6991   25.2907   29.0251
   20.5909   25.1711   28.9066
   20.4828   25.0514   28.7881
   20.3746   24.9318   28.6696
   20.2664   24.8121   28.5512
   20.1583   24.6924   28.4327
   20.0501   24.5728   28.3142
   19.9419   24.4531   28.1957
   19.8337   24.3335   28.0772
      ⋮

For each observation in gridX, the predict object function returns predictions for the quantiles in Mdl.Quantiles.

View the gridY predictions for the second predictor (Displacement). Compare the quantile predictions to the true test data values.

predictorIdx = 2;
plot(XTest(:,predictorIdx),YTest,".")
hold on
plot(gridX(:,predictorIdx),gridY(:,1))
plot(gridX(:,predictorIdx),gridY(:,2))
plot(gridX(:,predictorIdx),gridY(:,3))
hold off
xlabel("Predictor (Displacement)")
ylabel("Response (MPG)")
legend(["True values","0.25 predicted values", ...
    "0.50 predicted values","0.75 predicted values"])
title("Test Data")

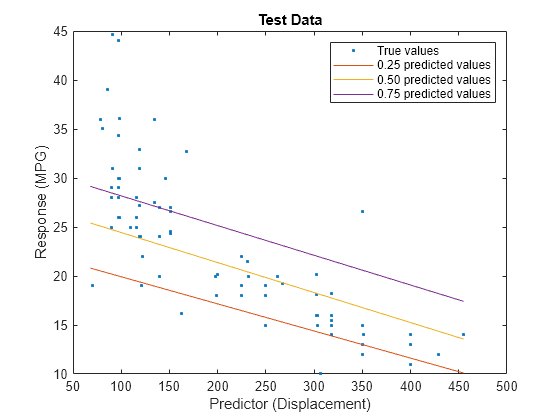
Figure contains an axes object. The axes object with title Test Data, xlabel Predictor (Displacement), ylabel Response (MPG) contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent True values, 0.25 predicted values, 0.50 predicted values, 0.75 predicted values.

The red line shows the predictions for the 0.25 quantile, the yellow line shows the predictions for the 0.50 quantile, and the purple line shows the predictions for the 0.75 quantile. The blue points indicate the true test data values.

Notice that the quantile prediction lines do not cross each other.

Fit Quantile Linear Regression Model to Data with Outliers

Open Live Script

Fit a quantile linear regression model to data with outliers using the median (0.5 quantile). Because the median is less influenced by outliers than the mean, using the fitrqlinear function can be a good alternative to using the fitrlinear function when fitting a linear model to data with outliers.

load carbig
X = [Acceleration,Displacement,Horsepower,Weight];
Y = MPG;

Delete rows of X and Y where either array has missing values.

R = rmmissing([X Y]);
X = R(:,1:end-1);
Y = R(:,end);

Visualize the data using the parallelplot function. The lines in the parallel coordinates plot correspond to individual cars, and the coordinate variables in the plot correspond to variables in the data.

p = parallelplot([X,Y]);
p.CoordinateTickLabels = ["Acceleration","Displacement", ...
    "Horsepower","Weight","MPG"];

Figure contains an object of type parallelplot.

You can use the plot to observe trends in the data. For example, Weight and MPG appear to be inversely related.

For this example, create an outlier and add it to the data in X and Y. Choose predictor values that are in the middle of the predictor ranges and an MPG value that is much higher than the other response values.

outlierCar = [16 250 140 3500];
outlierCarMPG = 75;
X = [X; outlierCar];
Y = [Y; outlierCarMPG];

Train a quantile linear regression model using the data in X and Y. By default, the model uses the median (or 0.5 quantile). To improve the model fit, change the beta tolerance to 1e-6 instead of the default value 1e-4.

medianMdl = fitrqlinear(X,Y,BetaTolerance=1e-6)

medianMdl = 
  RegressionQuantileLinear
             ResponseName: 'Y'
    CategoricalPredictors: []
        ResponseTransform: 'none'
                     Beta: [4x1 double]
                     Bias: 22.7505
                Quantiles: 0.5000

medianMdl is a RegressionQuantileLinear model object.

For comparison, train a linear regression model with the same training data using fitrlinear.

meanMdl = fitrlinear(X,Y,BetaTolerance=1e-6)

meanMdl = 
  RegressionLinear
         ResponseName: 'Y'
    ResponseTransform: 'none'
                 Beta: [4x1 double]
                 Bias: 22.8062
               Lambda: 0.0025
              Learner: 'svm'

meanMdl is a RegressionLinear model object.

Visualize the predictive behavior of the two models. First, create a grid of predictor values.

minX = floor(min(X));
maxX = ceil(max(X));
gridX = zeros(100,size(X,2));
for p = 1:size(X,2)
    gridp = linspace(minX(p),maxX(p))';
    gridX(:,p) = gridp;
end

Next, predict the response values for the grid of predictor values using the trained models.

medianGridY = predict(medianMdl,gridX);
meanGridY = predict(meanMdl,gridX);

Visualize the predictions for the third predictor (Horsepower). Compare the predictions to the true data values.

predictorIdx = 3;
plot(X(:,predictorIdx),Y,".")
hold on
plot(gridX(:,predictorIdx),medianGridY)
plot(gridX(:,predictorIdx),meanGridY)
hold off
legend(["True Values","Median","Mean"])
xlabel("Predictor (Horsepower)")
ylabel("Response (MPG)")
legend(["True values (with outlier)","Median predictions", ...
    "Mean predictions"],Location="northwest")
title("Training Data")

Figure contains an axes object. The axes object with title Training Data, xlabel Predictor (Horsepower), ylabel Response (MPG) contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent True values (with outlier), Median predictions, Mean predictions.

The red line shows the predictions made by the predict object function of medianMdl, and the yellow line shows the predictions made by the predict object function of meanMdl. The blue points indicate the true data values with the outlier included.

The red line better captures the relationship between Horsepower and MPG.

Prevent Quantile Crossing Using Regularization

Open Live Script

When training a quantile linear regression model, you can use a ridge (L2) regularization term to prevent quantile crossing.

Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a table containing the predictor variables Acceleration, Cylinders, Displacement, and so on, as well as the response variable MPG.

load carbig
cars = table(Acceleration,Cylinders,Displacement, ...
    Horsepower,Model_Year,Weight,MPG);

Remove rows of cars where the table has missing values.

cars = rmmissing(cars);

Partition the data into training and test sets using cvpartition. Use approximately 80% of the observations as training data, and 20% of the observations as test data.

rng(0,"twister") % For reproducibility of the data partition
c = cvpartition(height(cars),"Holdout",0.20);

trainingIdx = training(c);
carsTrain = cars(trainingIdx,:);

testIdx = test(c);
carsTest = cars(testIdx,:);

Train a quantile linear regression model. Use the 0.25, 0.50, and 0.75 quantiles (that is, the lower quartile, median, and upper quartile). To improve the model fit, change the beta tolerance to 1e-6 instead of the default value 1e-4.

Mdl = fitrqlinear(carsTrain,"MPG",Quantiles=[0.25 0.5 0.75], ...
    BetaTolerance=1e-6);

Mdl is a RegressionQuantileLinear model object.

Determine if the test data predictions for the quantiles in Mdl.Quantiles cross each other by using the predict object function of Mdl. The crossingIndicator output argument contains a value of 1 (true) for any observation with quantile predictions that cross.

[~,crossingIndicator] = predict(Mdl,carsTest);
sum(crossingIndicator)

ans = 
2

In this example, two of the observations in carsTest have quantile predictions that cross each other.

To prevent quantile crossing, specify the Lambda name-value argument in the call to fitrqlinear. Use a 0.1 ridge (L2) penalty term.

newMdl = fitrqlinear(carsTrain,"MPG",Quantiles=[0.25 0.5 0.75], ...
    BetaTolerance=1e-6,Lambda=0.1);
[predictedY,newCrossingIndicator] = predict(newMdl,carsTest);
sum(newCrossingIndicator)

ans = 
0

With regularization, the predictions for the test data set do not cross for any observations.

Visualize the predictions returned by newMdl by using a scatter plot with a reference line. Plot the predicted values along the vertical axis and the true response values along the horizontal axis. Points on the reference line indicate correct predictions.

plot(carsTest.MPG,predictedY(:,1),".")
hold on
plot(carsTest.MPG,predictedY(:,2),".")
plot(carsTest.MPG,predictedY(:,3),".")
plot(carsTest.MPG,carsTest.MPG)
hold off
xlabel("True MPG")
ylabel("Predicted MPG")
legend(["0.25 quantile values","0.50 quantile values", ...
    "0.75 quantile values","Reference line"], ...
    Location="southeast")
title("Test Data")

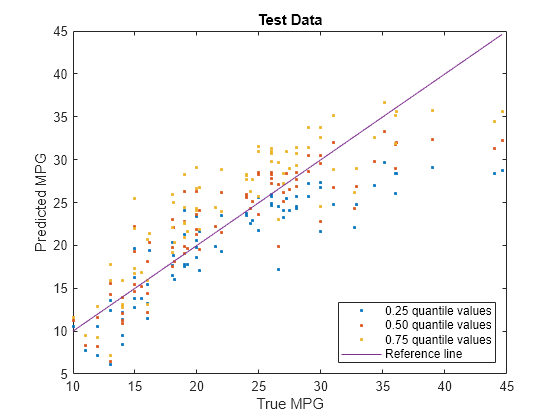
Figure contains an axes object. The axes object with title Test Data, xlabel True MPG, ylabel Predicted MPG contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent 0.25 quantile values, 0.50 quantile values, 0.75 quantile values, Reference line.

Blue points correspond to the 0.25 quantile, red points correspond to the 0.50 quantile, and yellow points correspond to the 0.75 quantile.

Input Arguments

collapse all

`Tbl` — Sample data
table

Sample data used to train the model, specified as a table. Each row of Tbl corresponds to one observation, and each column corresponds to one predictor variable. Optionally, Tbl can contain one additional column for the response variable. Multicolumn variables and cell arrays other than cell arrays of character vectors are not allowed.

If Tbl contains the response variable, and you want to use all remaining variables in Tbl as predictors, then specify the response variable by using ResponseVarName.
If Tbl contains the response variable, and you want to use only a subset of the remaining variables in Tbl as predictors, then specify a formula by using formula.
If Tbl does not contain the response variable, then specify a response variable by using Y. The length of the response variable and the number of rows in Tbl must be equal.

`ResponseVarName` — Response variable name
name of variable in `Tbl`

Response variable name, specified as the name of a variable in Tbl. The response variable must be a numeric vector.

You must specify ResponseVarName as a character vector or string scalar. For example, if Tbl stores the response variable Y as Tbl.Y, then specify it as "Y". Otherwise, the software treats all columns of Tbl, including Y, as predictors when training the model.

Data Types: char | string

`formula` — Explanatory model of response variable and subset of predictor variables
character vector | string scalar

Explanatory model of the response variable and a subset of the predictor variables, specified as a character vector or string scalar in the form "Y~x1+x2+x3". In this form, Y represents the response variable, and x1, x2, and x3 represent the predictor variables.

To specify a subset of variables in Tbl as predictors for training the model, use a formula. If you specify a formula, then the software does not use any variables in Tbl that do not appear in formula.

The variable names in the formula must be both variable names in Tbl (Tbl.Properties.VariableNames) and valid MATLAB^® identifiers. You can verify the variable names in Tbl by using the isvarname function. If the variable names are not valid, then you can convert them by using the matlab.lang.makeValidName function.

Data Types: char | string

`Y` — Response data
numeric vector

Response data, specified as an n-dimensional numeric vector. The length of Y must be equal to the number of observations in X or Tbl.

Data Types: single | double

`X` — Predictor data
numeric matrix

Predictor data used to train the model, specified as a numeric matrix.

By default, the software treats each row of X as one observation, and each column as one predictor.

The length of Y and the number of observations in X must be equal.

To specify the names of the predictors in the order of their appearance in X, use the PredictorNames name-value argument.

Note

If you orient your predictor matrix so that observations correspond to columns and specify ObservationsIn="columns", then you might experience a significant reduction in computation time.

Data Types: single | double

Note

The software treats NaN, empty character vector (''), empty string (""), <missing>, and <undefined> elements as missing values, and removes observations with any of these characteristics:

Missing value in the response
At least one missing value in a predictor observation
NaN value or 0 weight

For economical memory usage, a best practice is to manually remove training observations that contain missing values before passing the data to fitrqlinear.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: fitrqlinear(Tbl,"MPG",Quantiles=[0.25 0.5 0.75],Standardize=true) specifies to use the 0.25, 0.5, and 0.75 quantiles and to standardize the data before training.

Linear Regression Options

collapse all

`Quantiles` — Quantiles
`0.5` (default) | vector of values in the range [0,1]

Quantiles to use for training Mdl, specified as a vector of values in the range [0,1]. For each quantile q, the function fits a linear regression model that separates the bottom 100*q percent of training responses from the top 100*(1 – q) percent of training responses.

You can find the estimated linear model coefficients and estimated bias term for each quantile in the Beta and Bias properties of Mdl, respectively.

Example: Quantiles=[0.25 0.5 0.75]

Data Types: single | double

`Beta` — Initial coefficient estimates
numeric matrix

Initial coefficient estimates, specified as a p-by-q numeric matrix. p is the number of predictor variables after dummy variables are created for categorical variables (for more details, see CategoricalPredictors), and q is the number of quantiles (for more details, see Quantiles).

By default, Beta is a matrix of 0 values.

Data Types: single | double

`Bias` — Initial intercept estimates
numeric vector

Initial intercept estimates, specified as a numeric vector of length q, where q is the number of quantiles (for more details, see Quantiles).

By default, the initial bias for each quantile is the corresponding weighted quantile of the response.

Data Types: single | double

`FitBias` — Flag to include linear model intercept
`true` (default) | `false`

Flag to include the linear model intercept, specified as true or false.

Value	Description
`true`	For each quantile, the software includes the bias term b in the linear model, and then estimates it.
`false`	The software sets b = 0 during estimation.

Example: FitBias=false

Data Types: logical

`Lambda` — Regularization term strength
`0` (default) | `"auto"` | nonnegative scalar

Regularization term strength, specified as "auto" or a nonnegative scalar. If you specify Lambda as "auto", then fitrqlinear uses 1/n as the regularization term strength, where n is the number of observations in X or Tbl.

Example: Lambda=1e-4

Data Types: single | double | char | string

`ObservationsIn` — Predictor data observation dimension
`"rows"` (default) | `"columns"`

Predictor data observation dimension, specified as "rows" or "columns".

Note

If you orient your predictor matrix so that observations correspond to columns and specify ObservationsIn="columns", then you might experience a significant reduction in computation time. You cannot specify ObservationsIn="columns" for predictor data in a table.

Example: ObservationsIn="columns"

Data Types: char | string

`Solver` — Objective function minimization technique for training
`"bfgs"` | `"lbfgs"`

Objective function minimization technique for training, specified as "bfgs" or "lbfgs".

If X or Tbl contains 100 or fewer predictors, then the default value is "bfgs".
Otherwise, the default value is "lbfgs".

Example: Solver="bfgs"

Data Types: char | string

`Standardize` — Flag to standardize predictor data
`false` or `0` (default) | `true` or `1`

Flag to standardize the predictor data, specified as a numeric or logical 0 (false) or 1 (true). If you set Standardize to true, then the software centers and scales each numeric predictor variable by the corresponding column mean and standard deviation. The software does not standardize categorical predictors.

Example: Standardize=true

Data Types: single | double | logical

Convergence Control Options

collapse all

`Verbose` — Verbosity level
`0` (default) | nonnegative integer

Verbosity level, specified as a nonnegative integer. Verbose controls the amount of diagnostic information fitrqlinear displays at the command line.

Value	Description
`0`	`fitrqlinear` does not display diagnostic information.
`1`	`fitrqlinear` periodically displays and stores the value of the objective function, gradient magnitude, and other diagnostic information.
Any other positive integer	`fitrqlinear` displays and stores diagnostic information at each training process iteration.

Example: Verbose=1

Data Types: single | double

`BetaTolerance` — Relative tolerance on linear coefficients and bias term
`1e-4` (default) | nonnegative scalar

Relative tolerance on the linear coefficients and the bias term (intercept) for each quantile, specified as a nonnegative scalar.

Let $B_{t} = [β_{t}^{'} b_{t}]$ , that is, the vector of the coefficients and the bias term at iteration t of the training process. If ${‖ \frac{B_{t} - B_{t - 1}}{B_{t}} ‖}_{2} < BetaTolerance$ , then the training process terminates.

Example: BetaTolerance=1e-6

Data Types: single | double

`GradientTolerance` — Absolute gradient tolerance
`1e-6` (default) | nonnegative scalar

Absolute gradient tolerance for each quantile, specified as a nonnegative scalar.

Let $\nabla ℒ_{t}$ be the gradient vector of the objective function with respect to the coefficients and bias term at iteration t of the training process. If ${‖ \nabla ℒ_{t} ‖}_{\infty} = \max | \nabla ℒ_{t} | < GradientTolerance$ , then the training process terminates.

If you also specify BetaTolerance, then the training process terminates when fitrqlinear satisfies either stopping criterion.

Example: GradientTolerance=eps

Data Types: single | double

`HessianHistorySize` — Size of history buffer for Hessian approximation
`15` (default) | positive integer

Size of the history buffer for the Hessian approximation, specified as a positive integer. At each iteration, the software constructs the Hessian using statistics from the latest HessianHistorySize iterations.

Example: HessianHistorySize=10

Data Types: single | double

`IterationLimit` — Maximal number of iterations
`1000` (default) | positive integer

Maximal number of iterations in the training process for each quantile, specified as a positive integer.

Example: IterationLimit=1e7

Data Types: single | double

Other Regression Options

collapse all

`CategoricalPredictors` — Categorical predictors list
vector of positive integers | logical vector | character matrix | string array | cell array of character vectors | `"all"`

Categorical predictors list, specified as one of the values in this table. The descriptions assume that the predictor data has observations in rows and predictors in columns.

Value	Description
Vector of positive integers	Each entry in the vector is an index value indicating that the corresponding predictor is categorical. The index values are between 1 and `p`, where `p` is the number of predictors used to train the model. If `fitrqlinear` uses a subset of input variables as predictors, then the function indexes the predictors using only the subset. The `CategoricalPredictors` values do not count any response variable, observation weights variable, or other variable that the function does not use.
Logical vector	A `true` entry means that the corresponding predictor is categorical. The length of the vector is `p`.
Character matrix	Each row of the matrix is the name of a predictor variable. The names must match the entries in `PredictorNames`. Pad the names with extra blanks so each row of the character matrix has the same length.
String array or cell array of character vectors	Each element in the array is the name of a predictor variable. The names must match the entries in `PredictorNames`.
`"all"`	All predictors are categorical.

By default, if the predictor data is in a table (Tbl), fitrqlinear assumes that a variable is categorical if it is a logical vector, categorical vector, character array, string array, or cell array of character vectors. If the predictor data is a matrix (X), fitrqlinear assumes that all predictors are continuous. To identify any other predictors as categorical predictors, specify them by using the CategoricalPredictors name-value argument.

For the identified categorical predictors, fitrqlinear creates dummy variables using two different schemes, depending on whether a categorical variable is unordered or ordered. For an unordered categorical variable, fitrqlinear creates one dummy variable for each level of the categorical variable. For an ordered categorical variable, fitrqlinear creates one less dummy variable than the number of categories. For details, see Automatic Creation of Dummy Variables.

Example: CategoricalPredictors="all"

`PredictorNames` — Predictor variable names
string array of unique names | cell array of unique character vectors

Predictor variable names, specified as a string array of unique names or cell array of unique character vectors. The functionality of PredictorNames depends on the way you supply the training data.

If you supply X and Y, then you can use PredictorNames to assign names to the predictor variables in X.
- The order of the names in PredictorNames must correspond to the predictor order in X. Assuming that X has the default orientation, with observations in rows and predictors in columns, PredictorNames{1} is the name of X(:,1), PredictorNames{2} is the name of X(:,2), and so on. Also, size(X,2) and numel(PredictorNames) must be equal.
- By default, PredictorNames is {'x1','x2',...}.
If you supply Tbl, then you can use PredictorNames to choose which predictor variables to use in training. That is, fitrqlinear uses only the predictor variables in PredictorNames and the response variable during training.
- PredictorNames must be a subset of Tbl.Properties.VariableNames and cannot include the name of the response variable.
- By default, PredictorNames contains the names of all predictor variables.
- A good practice is to specify the predictors for training using either PredictorNames or formula, but not both.

Example: PredictorNames=["SepalLength","SepalWidth","PetalLength","PetalWidth"]

Data Types: string | cell

`ResponseName` — Response variable name
`"Y"` (default) | character vector | string scalar

Response variable name, specified as a character vector or string scalar.

If you supply Y, then you can use ResponseName to specify a name for the response variable.
If you supply ResponseVarName or formula, then you cannot use ResponseName.

Example: ResponseName="response"

Data Types: char | string

`ResponseTransform` — Function for transforming raw response values
`"none"` (default) | function handle | function name

Function for transforming raw response values, specified as a function handle or function name. The default is "none", which means @(y)y, or no transformation. The function should accept a vector (the original response values) and return a vector of the same size (the transformed response values).

Example: Suppose you create a function handle that applies an exponential transformation to an input vector by using myfunction = @(y)exp(y). Then, you can specify the response transformation as ResponseTransform=myfunction.

Data Types: char | string | function_handle

`Weights` — Observation weights
nonnegative numeric vector | name of variable in `Tbl`

Observation weights, specified as a nonnegative numeric vector or the name of a variable in Tbl. The software weights each observation in X or Tbl with the corresponding value in Weights. The length of Weights must equal the number of observations in X or Tbl.

If you specify the input data as a table Tbl, then Weights can be the name of a variable in Tbl that contains a numeric vector. In this case, you must specify Weights as a character vector or string scalar. For example, if the weights vector W is stored as Tbl.W, then specify it as "W". Otherwise, the software treats all columns of Tbl, including W, as predictors when training the model.

By default, Weights is ones(n,1), where n is the number of observations in X or Tbl.

fitrqlinear normalizes the weights to sum to 1.

Data Types: single | double | char | string

Output Arguments

collapse all

`Mdl` — Trained quantile linear regression model
`RegressionQuantileLinear` model object

Trained quantile linear regression model, returned as a RegressionQuantileLinear model object.

To reference properties of Mdl, use dot notation.

Tips

You can use the α/2 and 1 – α/2 quantiles to create a prediction interval that captures an estimated 100*(1 – α) percent of the variation in the response.

Version History

Introduced in R2024b

fitrqlinear

Syntax

Description

Examples

Fit Quantile Linear Regression Model

Fit Quantile Linear Regression Model to Data with Outliers

Prevent Quantile Crossing Using Regularization

Input Arguments

Tbl — Sample data table

ResponseVarName — Response variable name name of variable in Tbl

formula — Explanatory model of response variable and subset of predictor variables character vector | string scalar

Y — Response data numeric vector

X — Predictor data numeric matrix

Name-Value Arguments

Quantiles — Quantiles 0.5 (default) | vector of values in the range [0,1]

Beta — Initial coefficient estimates numeric matrix

Bias — Initial intercept estimates numeric vector

FitBias — Flag to include linear model intercept true (default) | false

Lambda — Regularization term strength 0 (default) | "auto" | nonnegative scalar

ObservationsIn — Predictor data observation dimension "rows" (default) | "columns"

Solver — Objective function minimization technique for training "bfgs" | "lbfgs"

Standardize — Flag to standardize predictor data false or 0 (default) | true or 1

Verbose — Verbosity level 0 (default) | nonnegative integer

BetaTolerance — Relative tolerance on linear coefficients and bias term 1e-4 (default) | nonnegative scalar

GradientTolerance — Absolute gradient tolerance 1e-6 (default) | nonnegative scalar

HessianHistorySize — Size of history buffer for Hessian approximation 15 (default) | positive integer

IterationLimit — Maximal number of iterations 1000 (default) | positive integer

CategoricalPredictors — Categorical predictors list vector of positive integers | logical vector | character matrix | string array | cell array of character vectors | "all"

PredictorNames — Predictor variable names string array of unique names | cell array of unique character vectors

ResponseName — Response variable name "Y" (default) | character vector | string scalar

ResponseTransform — Function for transforming raw response values "none" (default) | function handle | function name

Weights — Observation weights nonnegative numeric vector | name of variable in Tbl

Output Arguments

Mdl — Trained quantile linear regression model RegressionQuantileLinear model object

Tips

Version History

See Also

`Tbl` — Sample data
table

`ResponseVarName` — Response variable name
name of variable in `Tbl`

`formula` — Explanatory model of response variable and subset of predictor variables
character vector | string scalar

`Y` — Response data
numeric vector

`X` — Predictor data
numeric matrix

`Quantiles` — Quantiles
`0.5` (default) | vector of values in the range [0,1]

`Beta` — Initial coefficient estimates
numeric matrix

`Bias` — Initial intercept estimates
numeric vector

`FitBias` — Flag to include linear model intercept
`true` (default) | `false`

`Lambda` — Regularization term strength
`0` (default) | `"auto"` | nonnegative scalar

`ObservationsIn` — Predictor data observation dimension
`"rows"` (default) | `"columns"`

`Solver` — Objective function minimization technique for training
`"bfgs"` | `"lbfgs"`

`Standardize` — Flag to standardize predictor data
`false` or `0` (default) | `true` or `1`

`Verbose` — Verbosity level
`0` (default) | nonnegative integer

`BetaTolerance` — Relative tolerance on linear coefficients and bias term
`1e-4` (default) | nonnegative scalar

`GradientTolerance` — Absolute gradient tolerance
`1e-6` (default) | nonnegative scalar

`HessianHistorySize` — Size of history buffer for Hessian approximation
`15` (default) | positive integer

`IterationLimit` — Maximal number of iterations
`1000` (default) | positive integer

`CategoricalPredictors` — Categorical predictors list
vector of positive integers | logical vector | character matrix | string array | cell array of character vectors | `"all"`

`PredictorNames` — Predictor variable names
string array of unique names | cell array of unique character vectors

`ResponseName` — Response variable name
`"Y"` (default) | character vector | string scalar

`ResponseTransform` — Function for transforming raw response values
`"none"` (default) | function handle | function name

`Weights` — Observation weights
nonnegative numeric vector | name of variable in `Tbl`

`Mdl` — Trained quantile linear regression model
`RegressionQuantileLinear` model object