使用 Symbolic Math Toolbox 进行解析绘图

Symbolic Math Toolbox™ 提供数学表达式的解析绘图，而无需显式生成数值数据。这些绘图可以用二维或三维的线条、曲线、等高线、曲面或网格形式呈现。

本文中的示例介绍了以下图形函数，这些函数接受符号函数、表达式和方程作为输入：

fplot
fimplicit
fcontour
fplot3
fsurf
fmesh
fimplicit3

使用 `fplot` 绘制显函数 $y = f (x)$

绘制函数 $\sin (\exp (x))$ 。

syms x
fplot(sin(exp(x)))

Figure contains an axes object. The axes object contains an object of type functionline.

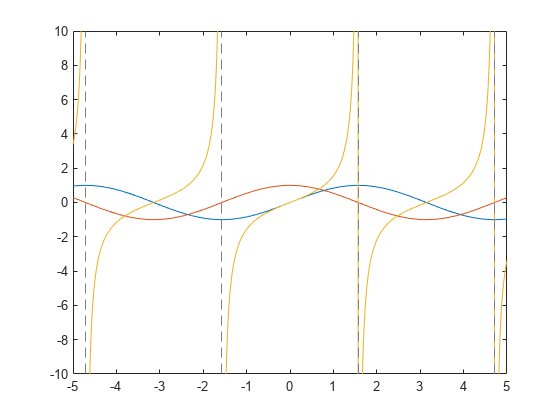
同时绘制三角函数 $\sin (x)$ 、 $\cos (x)$ 和 $\tan (x)$ 。

fplot([sin(x),cos(x),tan(x)])

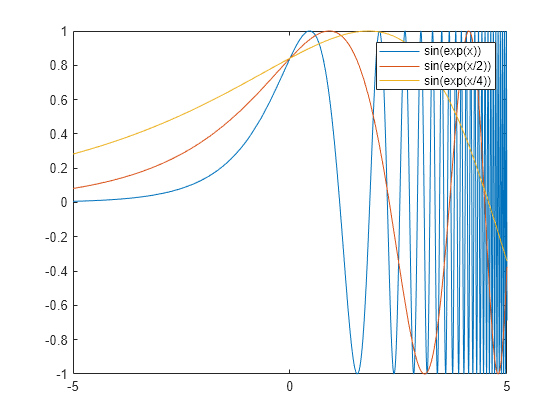
Figure contains an axes object. The axes object contains 3 objects of type functionline.

绘制由 $y = f (x, a)$ 定义的函数，其中 $a$ 采用不同值

绘制函数 $\sin (\exp (x / a))$ 在 $a = 1$ 、 $2$ 和 $4$ 时的图。

syms x a
expr = sin(exp(x/a));
fplot(subs(expr,a,[1,2,4]))
legend show

Figure contains an axes object. The axes object contains 3 objects of type functionline.

绘制函数的导数和积分

绘制函数 $f (x) = x (1 + x) + 2$ 、其导数 $d f (x) / d x$ 及其积分 $\int f (x) d x$ 。

syms f(x)
f(x) = x*(1 + x) + 2

f(x) =  $x (x + 1) + 2$

f_diff = diff(f(x),x)

f_diff =  $2 x + 1$

f_int = int(f(x),x)

f_int = 
 $\frac{x (2 x^{2} + 3 x + 12)}{6}$

fplot([f,f_diff,f_int])
legend({'$f(x)$','$df(x)/dx$','$\int f(x)dx$'},'Interpreter','latex','FontSize',12)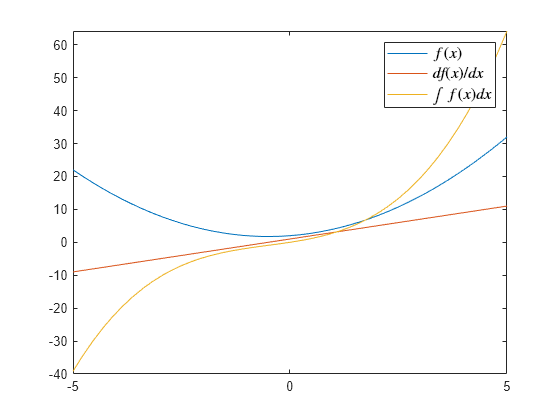

$Figure contains an axes object. The axes object contains 3 objects of type functionline. These objects represent $f(x)$, $df(x)/dx$, $\int f(x)dx$.$

以 $a$ 为水平轴绘制函数 $y = g (x_{0}, a)$

通过求解微分方程 $d g (x, a) / d x = 0$ ，得到最小化函数 $g (x, a)$ 的 $x_{0}$ 。

syms g(x,a);
assume(a>0);
g(x,a) = a*x*(a + x) + 2*sqrt(a)

g(x, a) =  $2 \sqrt{a} + a x (a + x)$

x0 = solve(diff(g,x),x)

x0 = 
 $- \frac{a}{2}$

绘制 $g (x_{0}, a)$ 的最小值，其中 $a$ 的范围为 0 到 5。

fplot(g(x0,a),[0 5])
xlabel('a')
title('Minimum Value of $g(x_0,a)$ Depending on $a$','interpreter','latex')

Figure contains an axes object. The axes object with title Minimum Value of g leftParenthesis x indexOf 0 baseline , a rightParenthesis Depending on a, xlabel a contains an object of type functionline.

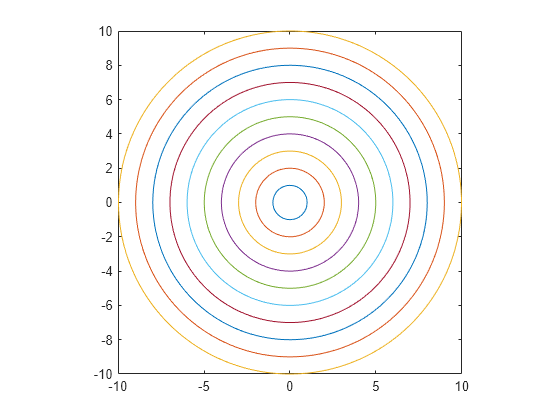
使用 `fimplicit` 绘制隐函数 $f (x, y) = c$

绘制由 $x^{2} + y^{2} = r^{2}$ 定义的圆，其中半径 $r$ 为 1 到 10 之间的整数。

syms x y
r = 1:10;
fimplicit(x^2 + y^2 == r.^2,[-10 10])
axis square;

Figure contains an axes object. The axes object contains 10 objects of type implicitfunctionline.

使用 `fcontour` 绘制函数 $f (x, y)$ 的等高线

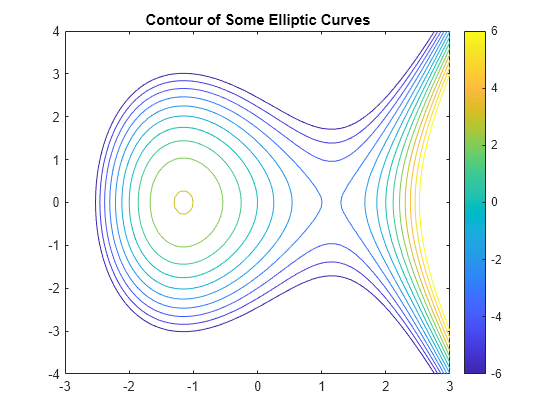
针对 –6 到 6 之间的等高线层级，绘制函数 $f (x, y) = x^{3} - 4 x - y^{2}$ 的等高线。

syms x y f(x,y)
f(x,y) = x^3 - 4*x - y^2;
fcontour(f,[-3 3 -4 4],'LevelList',-6:6);
colorbar
title 'Contour of Some Elliptic Curves'

Figure contains an axes object. The axes object with title Contour of Some Elliptic Curves contains an object of type functioncontour.

使用样条插值绘制解析函数及其逼近

绘制解析函数 $f (x) = x \exp (- x) \sin (5 x) - 2$ 。

syms f(x)
f(x) = x*exp(-x)*sin(5*x) -2;
fplot(f,[0,3])

从解析函数创建几个数据点。

xs = 0:1/3:3;
ys = double(subs(f,xs));

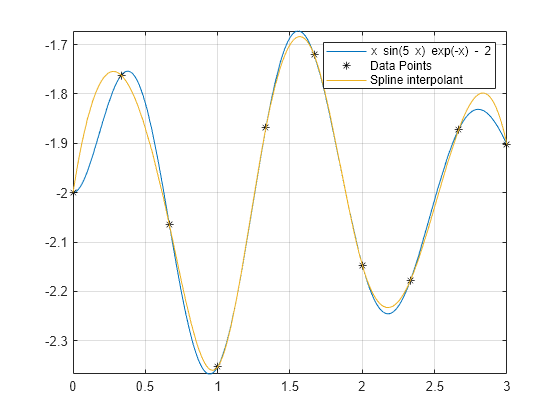
绘制这些数据点和逼近该解析函数的样条插值。

hold on
plot(xs,ys,'*k','DisplayName','Data Points')
fplot(@(x) spline(xs,ys,x),[0 3],'DisplayName','Spline interpolant')
grid on
legend show
hold off

Figure contains an axes object. The axes object contains 3 objects of type functionline, line. One or more of the lines displays its values using only markers These objects represent Data Points, Spline interpolant.

绘制函数的泰勒逼近

求 $\cos (x)$ 在 $x = 0$ 附近的泰勒展开式，直到 5 阶和 7 阶。

syms x
t5 = taylor(cos(x),x,'Order',5)

t5 = 
 $\frac{x^{4}}{24} - \frac{x^{2}}{2} + 1$

t7 = taylor(cos(x),x,'Order',7)

t7 = 
 $- \frac{x^{6}}{720} + \frac{x^{4}}{24} - \frac{x^{2}}{2} + 1$

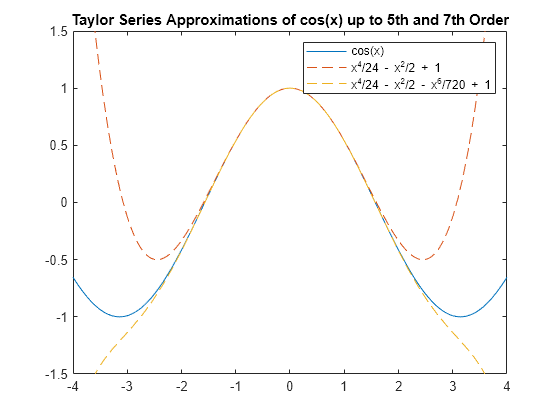
绘制 $\cos (x)$ 及其泰勒逼近。

fplot(cos(x))
hold on;
fplot([t5 t7],'--')
axis([-4 4 -1.5 1.5])
title('Taylor Series Approximations of cos(x) up to 5th and 7th Order')
legend show
hold off;

Figure contains an axes object. The axes object with title Taylor Series Approximations of cos(x) up to 5th and 7th Order contains 3 objects of type functionline.

绘制方波的傅里叶级数逼近

周期为 $2 π$ 、振幅为 $π / 4$ 的方波可通过傅里叶级数展开进行逼近

$\sin (t) + \frac{1}{3} \sin (3 t) + \frac{1}{5} \sin (5 t) + . . . .$

绘制周期为 $2 π$ 、振幅为 $π / 4$ 的方波。

syms t y(t)
y(t) = piecewise(0 < mod(t,2*pi) <= pi, pi/4, pi < mod(t,2*pi) <= 2*pi, -pi/4);
fplot(y)

绘制方波的傅里叶级数逼近。

hold on;
n = 6;
yFourier = cumsum(sin((1:2:2*n-1)*t)./(1:2:2*n-1));
fplot(yFourier,'LineWidth',1)
hold off

Figure contains an axes object. The axes object contains 7 objects of type functionline.

傅里叶级数逼近在跳跃间断处会出现过冲，并且随着更多项添加到逼近中，“振铃效应”不会消失。这种行为也称为吉布斯现象。

使用 `fplot3` 绘制参数化曲线 $(x (t), y (t), z (t))$

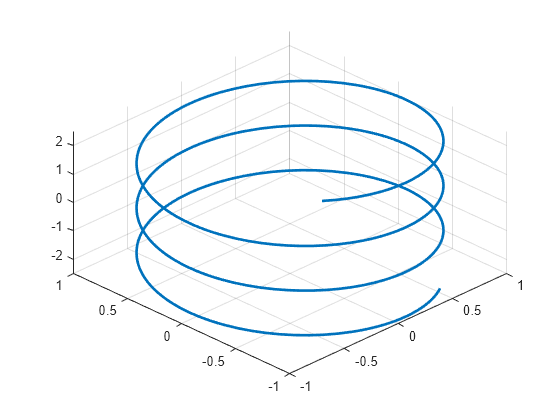
绘制由 $(\sin (t), \cos (t), t / 4)$ 定义的螺旋线，其中 $t$ 的范围为 –10 到 10。

syms t
fplot3(sin(t),cos(t),t/4,[-10 10],'LineWidth',2)
view([-45 45])

Figure contains an axes object. The axes object contains an object of type parameterizedfunctionline.

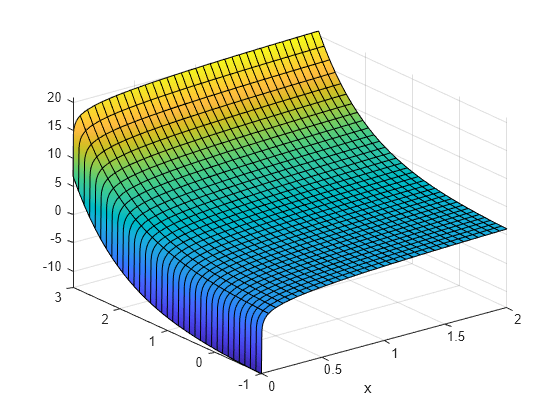
使用 `fsurf` 绘制由 $z = f (x, y)$ 定义的曲面

绘制由 $\log (x) + \exp (y)$ 定义的曲面。使用 fsurf 进行解析绘图（无需生成数值数据）可显示 $x = 0$ 附近的弯曲区域和渐近区域。

syms x y
fsurf(log(x) + exp(y),[0 2 -1 3])
xlabel('x')

Figure contains an axes object. The axes object with xlabel x contains an object of type functionsurface.

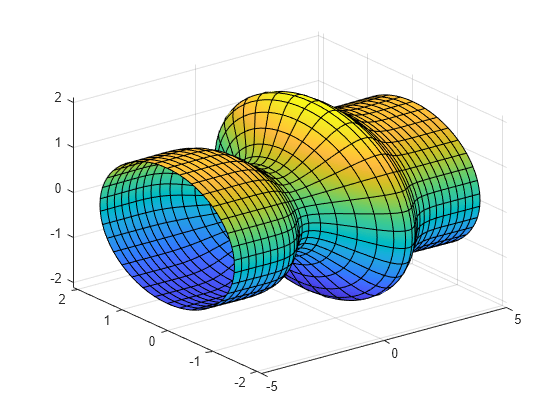
使用 `fsurf` 绘制多元曲面 $(x (u, v), y (u, v), z (u, v))$

绘制由以下各项定义的多元曲面：

$x (u, v) = u$

$y (u, v) = f (u) \sin (v)$

$z (u, v) = f (u) \cos (v)$

其中 $f (u) = \exp (- u^{2} / 3) \sin (u) + 3 / 2$ 。

将 $u$ 的绘图区间设置为 –5 到 5，并且将 $v$ 的绘图区间设置为 0 到 2 $π$ 。

syms f(u) x(u,v) y(u,v) z(u,v)
f(u) = sin(u)*exp(-u^2/3)+1.5;
x(u,v) = u;
y(u,v) = f(u)*sin(v);
z(u,v) = f(u)*cos(v);
fsurf(x,y,z,[-5 5 0 2*pi])

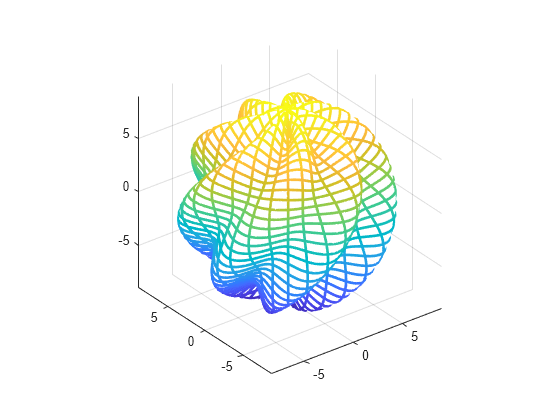
Figure contains an axes object. The axes object contains an object of type parameterizedfunctionsurface.

使用 `fmesh` 绘制多元曲面 $(x (s, t), y (s, t), z (s, t))$

绘制由以下各项定义的多元曲面：

$x = r \cos (s) \sin (t)$

$y = r \sin (s) \sin (t)$

$z = r \cos (t)$

其中 $r = 8 + \sin (7 s + 5 t)$ 。使用 fmesh 将绘制的曲面显示为网格。将 $s$ 的绘图区间设置为 0 到 2 $π$ ，并且将 $t$ 的绘图区间设置为 0 到 $π$ 。

syms s t
r = 8 + sin(7*s + 5*t);
x = r*cos(s)*sin(t);
y = r*sin(s)*sin(t);
z = r*cos(t);
fmesh(x,y,z,[0 2*pi 0 pi],'Linewidth',2)
axis equal

Figure contains an axes object. The axes object contains an object of type parameterizedfunctionsurface.

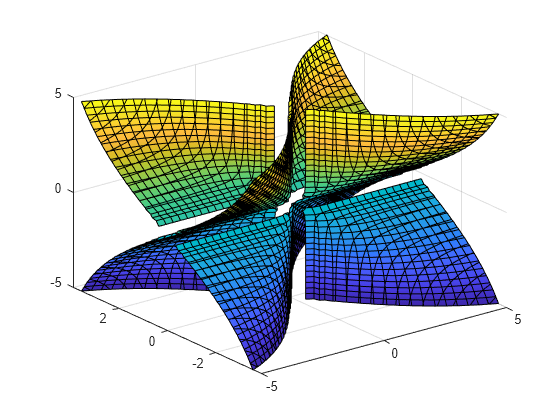
使用 `fimplicit3` 绘制隐式曲面 $f (x, y, z) = c$

绘制隐式曲面 $1 / x^{2} - 1 / y^{2} + 1 / z^{2} = 0$ 。

syms x y z
f = 1/x^2 - 1/y^2 + 1/z^2;
fimplicit3(f)

Figure contains an axes object. The axes object contains an object of type implicitfunctionsurface.

绘制曲面的等高线和梯度

使用 fsurf 绘制曲面 $\sin (x) + \sin (y) - (x^{2} + y^{2}) / 20$ 。您可以通过将 'ShowContours' 设置为 'on' 在同一图上显示等高线。

syms x y
f = sin(x)+sin(y)-(x^2+y^2)/20

f = 
 $\sin (x) + \sin (y) - \frac{x^{2}}{20} - \frac{y^{2}}{20}$

fsurf(f,'ShowContours','on')
view(-19,56)

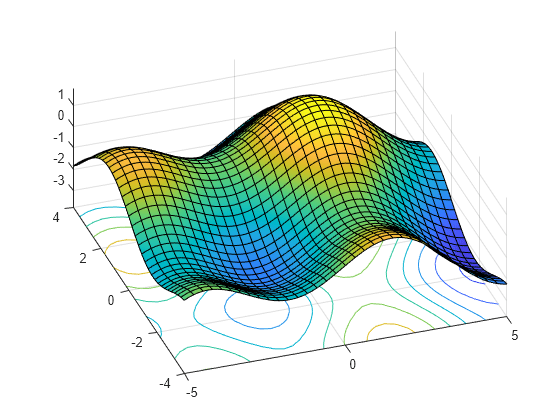
Figure contains an axes object. The axes object contains an object of type functionsurface.

接下来，在具有更精细等高线的单个图上绘制等高线。

fcontour(f,[-5 5 -5 5],'LevelStep',0.1,'Fill','on')
colorbar

找到曲面的梯度。使用 meshgrid 创建二维网格并代入网格坐标，以便通过数值方式计算梯度。使用 quiver 显示梯度。

hold on
Fgrad = gradient(f,[x,y])

Fgrad = 
 $(\begin{array}{c} \cos (x) - \frac{x}{10} \\ \cos (y) - \frac{y}{10} \end{array})$

[xgrid,ygrid] = meshgrid(-5:5,-5:5);
Fx = subs(Fgrad(1),{x,y},{xgrid,ygrid});
Fy = subs(Fgrad(2),{x,y},{xgrid,ygrid});
quiver(xgrid,ygrid,Fx,Fy,'k')
hold off

Figure contains an axes object. The axes object contains 2 objects of type functioncontour, quiver.

另请参阅

函数

fplot | fimplicit | fcontour | fplot3 | fsurf | fmesh | fimplicit3

使用 Symbolic Math Toolbox 进行解析绘图

使用 fplot 绘制显函数 y=f(x)

绘制由 y=f(x,a) 定义的函数，其中 a 采用不同值

绘制函数的导数和积分

以 a 为水平轴绘制函数 y=g(x0,a)

使用 fimplicit 绘制隐函数 f(x,y)=c

使用 fcontour 绘制函数 f(x,y) 的等高线