cot
Symbolic cotangent function
Syntax
Description
cot( returns the cotangent function of X)X.
Examples
Cotangent Function for Numeric and Symbolic Arguments
Depending on its arguments, cot returns
floating-point or exact symbolic results.
Compute the cotangent function for these numbers. Because these
numbers are not symbolic objects, cot returns
floating-point results.
A = cot([-2, -pi/2, pi/6, 5*pi/7, 11])
A =
0.4577 -0.0000 1.7321 -0.7975 -0.0044Compute the cotangent function for the numbers converted to
symbolic objects. For many symbolic (exact) numbers, cot returns
unresolved symbolic calls.
symA = cot(sym([-2, -pi/2, pi/6, 5*pi/7, 11]))
symA = [ -cot(2), 0, 3^(1/2), -cot((2*pi)/7), cot(11)]
Use vpa to approximate symbolic results
with floating-point numbers:
vpa(symA)
ans = [ 0.45765755436028576375027741043205,... 0,... 1.7320508075688772935274463415059,... -0.79747338888240396141568825421443,... -0.0044257413313241136855482762848043]
Plot Cotangent Function
Plot the cotangent function on the interval from to .
syms x fplot(cot(x),[-pi pi]) grid on
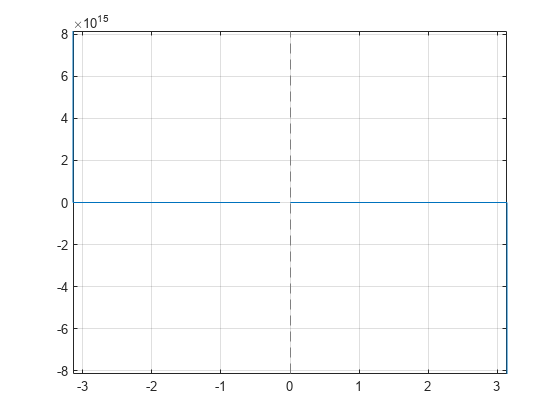
Handle Expressions Containing Cotangent Function
Many functions, such as diff, int, taylor,
and rewrite, can handle expressions containing cot.
Find the first and second derivatives of the cotangent function:
syms x diff(cot(x), x) diff(cot(x), x, x)
ans = - cot(x)^2 - 1 ans = 2*cot(x)*(cot(x)^2 + 1)
Find the indefinite integral of the cotangent function:
int(cot(x), x)
ans = log(sin(x))
Find the Taylor series expansion of cot(x) around x
= pi/2:
taylor(cot(x), x, pi/2)
ans = pi/2 - x - (x - pi/2)^3/3 - (2*(x - pi/2)^5)/15
Rewrite the cotangent function in terms of the sine and cosine functions:
rewrite(cot(x), 'sincos')
ans = cos(x)/sin(x)
Rewrite the cotangent function in terms of the exponential function:
rewrite(cot(x), 'exp')
ans = (exp(x*2i)*1i + 1i)/(exp(x*2i) - 1)
Evaluate Units with cot Function
cot numerically evaluates these units
automatically: radian, degree,
arcmin, arcsec, and
revolution.
Show this behavior by finding the cotangent of x
degrees and 2 radians.
u = symunit; syms x f = [x*u.degree 2*u.radian]; cotf = cot(f)
cotf = [ cot((pi*x)/180), cot(2)]
You can calculate cotf by substituting for
x using subs and then using
double or vpa.