求导

多变量表达式的导数

要对包含多个符号变量的表达式求导，需要指定要关于哪个变量求导。然后，diff 命令会计算该表达式关于该指定变量的偏导数。例如，指定一个包含两个变量的符号表达式。

syms s t
f = sin(s*t);

通过使用 diff 并指定求导变量为 t，求偏导数 $$\partial f/\partial t$$。

Df_t = diff(f,t)

Df_t = $$s\hspace{0.17em}\cos \left(s\hspace{0.17em}t\right)$$

要对 f 关于变量 s 求导，需要指定求导变量为 s。

Df_s = diff(f,s)

Df_s = $$t\hspace{0.17em}\cos \left(s\hspace{0.17em}t\right)$$

如果您不指定要关于哪个变量求导，diff 会使用默认变量。一般来说，默认变量是字母表中最接近 x 的字母。有关完整的规则，请参阅Find Symbolic Variables in Expressions, Functions, and Matrices。在前面的示例中，diff(f) 对 f 关于 t 求导，这是因为在字母表中字母 t 比字母 s 更接近 x。要确定 MATLAB® 求导时使用的默认变量，可使用 symvar。

fvar = symvar(f,1)

fvar = $$t$$

计算 f 关于 t 的二阶导数。

D2f = diff(f,t,2)

D2f = $$-s^2\hspace{0.17em}\sin \left(s\hspace{0.17em}t\right)$$

请注意，diff(f,2) 会返回相同的答案，因为 t 是默认变量。

关于导数的更多示例

为了进一步说明对其他表达式使用 diff 函数的情况，我们定义了以下符号变量 a、b、x、n、t 和 theta。

syms a b x n t theta

下表说明了对几个其他表达式使用 diff 的结果。

您可以对第一类贝塞尔函数 besselj(nu,z) 关于 z 求导。

syms nu z
b = besselj(nu,z);
Db = diff(b)

Db = 
$$\frac{\nu \hspace{0.17em}{\mathrm{J}\text{<a href="matlab:doc symbolic/besselj">besselj</a>}}_{\nu }\left(z\right)}{z}-{\mathrm{J}\text{<a href="matlab:doc symbolic/besselj">besselj</a>}}_{\nu +1}\left(z\right)$$

diff 函数也可以将符号矩阵作为其输入。在这种情况下，求导是逐个元素进行的。

syms a x
A = [cos(a*x),sin(a*x);-sin(a*x),cos(a*x)]

A = 
$$\left(\begin{array}{cc}\cos \left(a\hspace{0.17em}x\right)& \sin \left(a\hspace{0.17em}x\right)\\ -\sin \left(a\hspace{0.17em}x\right)& \cos \left(a\hspace{0.17em}x\right)\end{array}\right)$$

求 A 关于 x 的导数。

DA = diff(A)

DA = 
$$\left(\begin{array}{cc}-a\hspace{0.17em}\sin \left(a\hspace{0.17em}x\right)& a\hspace{0.17em}\cos \left(a\hspace{0.17em}x\right)\\ -a\hspace{0.17em}\cos \left(a\hspace{0.17em}x\right)& -a\hspace{0.17em}\sin \left(a\hspace{0.17em}x\right)\end{array}\right)$$

您还可以对向量函数关于向量参量进行求导。以笛卡尔坐标 $$(x,y,z)$$ 到球面坐标 $$(r,\lambda ,\phi )$$ 的变换为例，变换公式如下：

$$x=r\cos \lambda \cos \phi$$,

$$y=r\cos \lambda \sin \phi$$,

$$z=r\sin \lambda$$.

在本例中，$$\lambda$$ 对应于仰角或纬度，而 $$\phi$$ 表示方位角或经度。

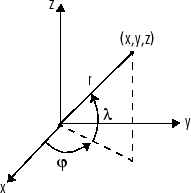
要计算这个变换的雅可比矩阵 $$J$$，请使用 jacobian 函数。$$J$$ 的数学表示法为

$$J=\frac{\partial (x,y,z)}{\partial (r,\lambda ,\phi )}$$.

为了计算雅可比矩阵，我们使用 l 表示 $$\lambda$$，使用 f 表示 $$\phi$$。求雅可比矩阵。

syms r l f
x = r*cos(l)*cos(f);
y = r*cos(l)*sin(f);
z = r*sin(l);
J = jacobian([x; y; z], [r l f])

J = 
$$\left(\begin{array}{ccc}\cos \left(f\right)\hspace{0.17em}\cos \left(l\right)& -r\hspace{0.17em}\cos \left(f\right)\hspace{0.17em}\sin \left(l\right)& -r\hspace{0.17em}\cos \left(l\right)\hspace{0.17em}\sin \left(f\right)\\ \cos \left(l\right)\hspace{0.17em}\sin \left(f\right)& -r\hspace{0.17em}\sin \left(f\right)\hspace{0.17em}\sin \left(l\right)& r\hspace{0.17em}\cos \left(f\right)\hspace{0.17em}\cos \left(l\right)\\ \sin \left(l\right)& r\hspace{0.17em}\cos \left(l\right)& 0\end{array}\right)$$

求这个雅可比矩阵的行列式并简化结果。

detJ = simplify(det(J))

detJ = $$-r^2\hspace{0.17em}\cos \left(l\right)$$

jacobian 函数的参量可以是列向量或行向量。此外，由于雅可比矩阵的行列式是一个相当复杂的三角函数表达式，因此，您可以使用 simplify 进行三角函数的代换和化简（简化）。

下面是一个总结 diff 和 jacobian 的表。