jacobiP
Jacobi polynomials
Syntax
Description
Examples
Find Jacobi Polynomials for Numeric and Symbolic Inputs
Find the Jacobi polynomial of degree 2 for
numeric inputs.
jacobiP(2,0.5,-3,6)
ans =
7.3438Find the Jacobi polynomial for symbolic inputs.
syms n a b x jacobiP(n,a,b,x)
ans = jacobiP(n, a, b, x)
If the degree of the Jacobi polynomial is not specified,
jacobiP cannot find the polynomial and returns the function
call.
Specify the degree of the Jacobi polynomial as 1 to return the
form of the polynomial.
J = jacobiP(1,a,b,x)
J = a/2 - b/2 + x*(a/2 + b/2 + 1)
To find the numeric value of a Jacobi polynomial, call
jacobiP with the numeric values directly. Do not substitute
into the symbolic polynomial because the result can be inaccurate due to round-off.
Test this by using subs to substitute into the symbolic
polynomial, and compare the result with a numeric call.
J = jacobiP(300, -1/2, -1/2, x); subs(J,x,vpa(1/2)) jacobiP(300, -1/2, -1/2, vpa(1/2))
ans = 101573673381249394050.64541318209 ans = 0.032559931334979678350422392588404
When subs is used to substitute into the symbolic polynomial,
the numeric result is subject to round-off error. The direct numerical call to
jacobiP is accurate.
Find Jacobi Polynomial with Vector and Matrix Inputs
Find the Jacobi polynomials of degrees 1
and 2 by setting n = [1 2] for a
= 3 and b = 1.
syms x jacobiP([1 2],3,1,x)
ans = [ 3*x + 1, 7*x^2 + (7*x)/2 - 1/2]
jacobiP acts on n element-wise to return a
vector with two entries.
If multiple inputs are specified as a vector, matrix, or multidimensional array,
these inputs must be the same size. Find the Jacobi polynomials for a = [1
2;3 1], b = [2 2;1 3], n = 1 and
x.
a = [1 2;3 1]; b = [2 2;1 3]; J = jacobiP(1,a,b,x)
J = [ (5*x)/2 - 1/2, 3*x] [ 3*x + 1, 3*x - 1]
jacobiP acts element-wise on a and
b to return a matrix of the same size as a
and b.
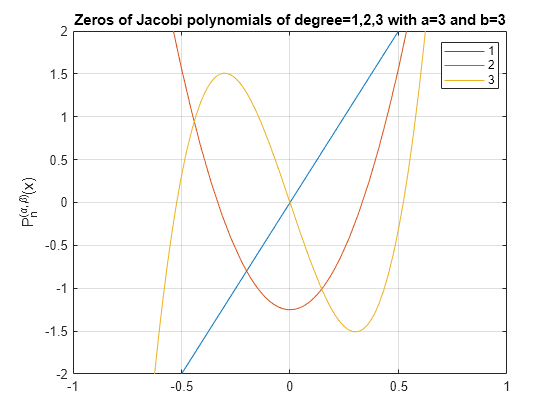
Visualize Zeros of Jacobi Polynomials
Plot Jacobi polynomials of degree 1, 2, and 3 for a = 3, b = 3, and -1<x<1. To better view the plot, set axis limits by using axis.
syms x fplot(jacobiP(1:3,3,3,x)) axis([-1 1 -2 2]) grid on ylabel('P_n^{(\alpha,\beta)}(x)') title('Zeros of Jacobi polynomials of degree=1,2,3 with a=3 and b=3'); legend('1','2','3','Location','best')
Prove Orthogonality of Jacobi Polynomials with Respect to Weight Function
The Jacobi polynomials P(n,a,b,x) are orthogonal with respect to the weight function on the interval [-1,1].
Prove P(3,a,b,x) and P(5,a,b,x) are orthogonal with respect to the weight function by integrating their product over the interval
[-1,1], where a = 3.5 and b =
7.2.
syms x a = 3.5; b = 7.2; P3 = jacobiP(3, a, b, x); P5 = jacobiP(5, a, b, x); w = (1-x)^a*(1+x)^b; int(P3*P5*w, x, -1, 1)
ans = 0
Input Arguments
More About
Version History
Introduced in R2014b
See Also
chebyshevT | chebyshevU | gegenbauerC | hermiteH | hypergeom | laguerreL | legendreP