laguerreL

Find Laguerre Polynomials for Numeric and Symbolic Inputs

Find the Laguerre polynomial of degree 3 for input 4.3.

laguerreL(3,4.3)

ans =
    2.5838

Find the Laguerre polynomial for symbolic inputs. Specify degree n as 3 to return the explicit form of the polynomial.

syms x
laguerreL(3,x)

ans =
- x^3/6 + (3*x^2)/2 - 3*x + 1

If the degree of the Laguerre polynomial n is not specified, laguerreL cannot find the polynomial. When laguerreL cannot find the polynomial, it returns the function call.

syms n x
laguerreL(n,x)

ans =
laguerreL(n, x)

Find Generalized Laguerre Polynomial

Find the explicit form of the generalized Laguerre polynomial L(n,a,x) of degree n = 2.

syms a x
laguerreL(2,a,x)

ans =
(3*a)/2 - x*(a + 2) + a^2/2 + x^2/2 + 1

Return Generalized Laguerre Function

When n is not a nonnegative integer, laguerreL(n,a,x) returns the generalized Laguerre function.

laguerreL(-2.7,3,2)

ans =
    0.2488

laguerreL is not defined for certain inputs and returns an error.

syms x
laguerreL(-5/2, -3/2, x)

Error using symengine
Function 'laguerreL' not supported for parameter values '-5/2' and '-3/2'.

Find Laguerre Polynomial with Vector and Matrix Inputs

Find the Laguerre polynomials of degrees 1 and 2 by setting n = [1 2].

syms x
laguerreL([1 2],x)

ans =
[ 1 - x, x^2/2 - 2*x + 1]

laguerreL acts element-wise on n to return a vector with two elements.

If multiple inputs are specified as a vector, matrix, or multidimensional array, the inputs must be the same size. Find the generalized Laguerre polynomials where input arguments n and x are matrices.

syms a
n = [2 3; 1 2];
xM = [x^2 11/7; -3.2 -x];
laguerreL(n,a,xM)

ans =
[ a^2/2 - a*x^2 + (3*a)/2 + x^4/2 - 2*x^2 + 1,...
      a^3/6 + (3*a^2)/14 - (253*a)/294 - 676/1029]
[                                    a + 21/5,...
          a^2/2 + a*x + (3*a)/2 + x^2/2 + 2*x + 1]

laguerreL acts element-wise on n and x to return a matrix of the same size as n and x.

Differentiate and Find Limits of Laguerre Polynomials

Use limit to find the limit of a generalized Laguerre polynomial of degree 3 as x tends to ∞.

syms x
expr = laguerreL(3,2,x);
limit(expr,x,Inf)

ans =
-Inf

Use diff to find the third derivative of the generalized Laguerre polynomial laguerreL(n,a,x).

syms n a
expr = laguerreL(n,a,x);
diff(expr,x,3)

ans =
-laguerreL(n - 3, a + 3, x)

Find Taylor Series Expansion of Laguerre Polynomials

Use taylor to find the Taylor series expansion of the generalized Laguerre polynomial of degree 2 at x = 0.

syms a x
expr = laguerreL(2,a,x);
taylor(expr,x)

ans =
(3*a)/2 - x*(a + 2) + a^2/2 + x^2/2 + 1

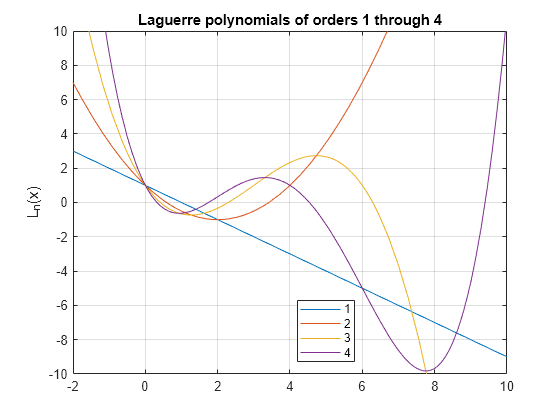
Plot Laguerre Polynomials

Plot the Laguerre polynomials of orders 1 through 4.

syms x
fplot(laguerreL(1:4,x))
axis([-2 10 -10 10])
grid on

ylabel('L_n(x)')
title('Laguerre polynomials of orders 1 through 4')
legend('1','2','3','4','Location','best')