Main Content

logp

Document log-probabilities and goodness of fit of LDA model

collapse all in page

Syntax

logProb = logp(ldaMdl,documents)
logProb = logp(ldaMdl,counts)
logProb = logp(ldaMdl,bag)
[logProb,ppl] = logp(___)
___ = logp(___,Name,Value)

Description

logProb = logp(ldaMdl,documents) returns the log-probabilities of documents under the LDA model ldaMdl.

example

logProb = logp(ldaMdl,counts) returns the log-probabilities of the documents represented by the matrix of word counts counts.

example

logProb = logp(ldaMdl,bag) returns the log-probabilities of the documents represented by a bag-of-words or bag-of-n-grams model.

[logProb,ppl] = logp(___) returns the perplexity computed from the log-probabilities.

example

___ = logp(___,Name,Value) specifies additional options using one or more name-value pair arguments.

Examples

collapse all

Open Live Script

To reproduce the results in this example, set rng to 'default'.

rng('default')

Load the example data. The file sonnetsPreprocessed.txt contains preprocessed versions of Shakespeare's sonnets. The file contains one sonnet per line, with words separated by a space. Extract the text from sonnetsPreprocessed.txt, split the text into documents at newline characters, and then tokenize the documents.

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Create a bag-of-words model using bagOfWords.

bag = bagOfWords(documents)
bag = 
  bagOfWords with properties:

          Counts: [154x3092 double]
      Vocabulary: ["fairest"    "creatures"    "desire"    "increase"    "thereby"    "beautys"    "rose"    "might"    "never"    "die"    "riper"    "time"    "decease"    "tender"    "heir"    "bear"    "memory"    "thou"    ...    ] (1x3092 string)
        NumWords: 3092
    NumDocuments: 154

Fit an LDA model with 20 topics. To suppress verbose output, set 'Verbose' to 0.

numTopics = 20;
mdl = fitlda(bag,numTopics,'Verbose',0);

Compute the document log-probabilities of the training documents and show them in a histogram.

logProbabilities = logp(mdl,documents);
figure
histogram(logProbabilities)
xlabel("Log Probability")
ylabel("Frequency")
title("Document Log-Probabilities")

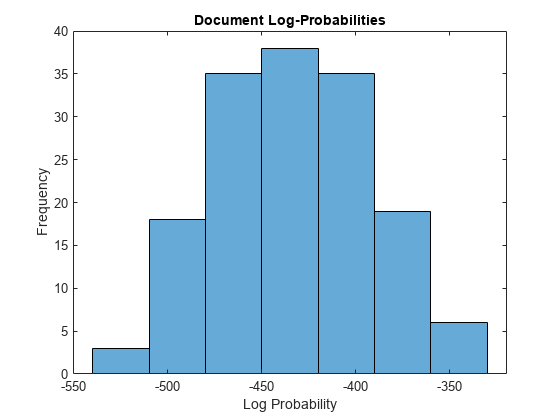
Figure contains an axes object. The axes object with title Document Log-Probabilities, xlabel Log Probability, ylabel Frequency contains an object of type histogram.

Identify the three documents with the lowest log-probability. A low log-probability may suggest that the document may be an outlier.

[~,idx] = sort(logProbabilities);
idx(1:3)
ans = 3×1

   146
    19
    65


documents(idx(1:3))
ans = 
  3x1 tokenizedDocument:

    76 tokens: poor soul centre sinful earth sinful earth rebel powers array why dost thou pine suffer dearth painting thy outward walls costly gay why large cost short lease dost thou upon thy fading mansion spend shall worms inheritors excess eat up thy charge thy bodys end soul live thou upon thy servants loss let pine aggravate thy store buy terms divine selling hours dross fed rich shall thou feed death feeds men death once dead theres dying
    76 tokens: devouring time blunt thou lions paws make earth devour own sweet brood pluck keen teeth fierce tigers jaws burn longlivd phoenix blood make glad sorry seasons thou fleets whateer thou wilt swiftfooted time wide world fading sweets forbid thee heinous crime o carve thy hours loves fair brow nor draw lines thine antique pen thy course untainted allow beautys pattern succeeding men yet thy worst old time despite thy wrong love shall verse ever live young
    73 tokens: brass nor stone nor earth nor boundless sea sad mortality oersways power rage shall beauty hold plea whose action stronger flower o shall summers honey breath hold against wrackful siege battering days rocks impregnable stout nor gates steel strong time decays o fearful meditation alack shall times best jewel times chest lie hid strong hand hold swift foot back spoil beauty forbid o none unless miracle might black ink love still shine bright
Open Live Script

Load the example data. sonnetsCounts.mat contains a matrix of word counts and a corresponding vocabulary of preprocessed versions of Shakespeare's sonnets. 

load sonnetsCounts.mat
size(counts)
ans = 1×2

         154        3092

Fit an LDA model with 20 topics.

numTopics = 20;
mdl = fitlda(counts,numTopics)
Initial topic assignments sampled in 0.052389 seconds.
=====================================================================================
| Iteration  |  Time per  |  Relative  |  Training  |     Topic     |     Topic     |
|            | iteration  | change in  | perplexity | concentration | concentration |
|            | (seconds)  |   log(L)   |            |               |   iterations  |
=====================================================================================
|          0 |       0.00 |            |  1.159e+03 |         5.000 |             0 |
|          1 |       0.02 | 5.4884e-02 |  8.028e+02 |         5.000 |             0 |
|          2 |       0.02 | 4.7400e-03 |  7.778e+02 |         5.000 |             0 |
|          3 |       0.02 | 3.4597e-03 |  7.602e+02 |         5.000 |             0 |
|          4 |       0.02 | 3.4662e-03 |  7.430e+02 |         5.000 |             0 |
|          5 |       0.02 | 2.9259e-03 |  7.288e+02 |         5.000 |             0 |
|          6 |       0.02 | 6.4180e-05 |  7.291e+02 |         5.000 |             0 |
=====================================================================================

mdl = 
  ldaModel with properties:

                     NumTopics: 20
             WordConcentration: 1
            TopicConcentration: 5
      CorpusTopicProbabilities: [0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500]
    DocumentTopicProbabilities: [154x20 double]
        TopicWordProbabilities: [3092x20 double]
                    Vocabulary: ["1"    "2"    "3"    "4"    "5"    "6"    "7"    "8"    "9"    "10"    "11"    "12"    "13"    "14"    "15"    "16"    "17"    "18"    "19"    "20"    "21"    "22"    "23"    "24"    "25"    ...    ] (1x3092 string)
                    TopicOrder: 'initial-fit-probability'
                       FitInfo: [1x1 struct]

Compute the document log-probabilities of the training documents. Specify to draw 500 samples for each document.

numSamples = 500;
logProbabilities = logp(mdl,counts, ...
    'NumSamples',numSamples);

Show the document log-probabilities in a histogram.

figure
histogram(logProbabilities)
xlabel("Log Probability")
ylabel("Frequency")
title("Document Log-Probabilities")

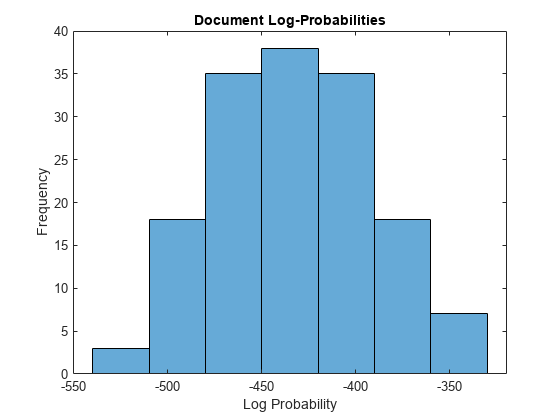
Figure contains an axes object. The axes object with title Document Log-Probabilities, xlabel Log Probability, ylabel Frequency contains an object of type histogram.

Identify the indices of the three documents with the lowest log-probability.

[~,idx] = sort(logProbabilities);
idx(1:3)
ans = 3×1

   146
    19
    65
Open Live Script

Compare the goodness of fit for two LDA models by calculating the perplexity of a held-out test set of documents.

To reproduce the results, set rng to 'default'.

rng('default')

Load the example data. The file sonnetsPreprocessed.txt contains preprocessed versions of Shakespeare's sonnets. The file contains one sonnet per line, with words separated by a space. Extract the text from sonnetsPreprocessed.txt, split the text into documents at newline characters, and then tokenize the documents.

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Set aside 10% of the documents at random for testing.

numDocuments = numel(documents);
cvp = cvpartition(numDocuments,'HoldOut',0.1);
documentsTrain = documents(cvp.training);
documentsTest = documents(cvp.test);

Create a bag-of-words model from the training documents.

bag = bagOfWords(documentsTrain)
bag = 
  bagOfWords with properties:

          Counts: [139x2909 double]
      Vocabulary: ["fairest"    "creatures"    "desire"    "increase"    "thereby"    "beautys"    "rose"    "might"    "never"    "die"    "riper"    "time"    "decease"    "tender"    "heir"    "bear"    "memory"    "thou"    ...    ] (1x2909 string)
        NumWords: 2909
    NumDocuments: 139

Fit an LDA model with 20 topics to the bag-of-words model. To suppress verbose output, set 'Verbose' to 0.

numTopics = 20;
mdl1 = fitlda(bag,numTopics,'Verbose',0);

View information about the model fit.

mdl1.FitInfo
ans = struct with fields:
          TerminationCode: 1
        TerminationStatus: "Relative tolerance on log-likelihood satisfied."
            NumIterations: 26
    NegativeLogLikelihood: 5.6915e+04
               Perplexity: 742.7118
                   Solver: "cgs"
                  History: [1x1 struct]

Compute the perplexity of the held-out test set.

[~,ppl1] = logp(mdl1,documentsTest)
ppl1 = 
781.6078

Fit an LDA model with 40 topics to the bag-of-words model.

numTopics = 40;
mdl2 = fitlda(bag,numTopics,'Verbose',0);

View information about the model fit.

mdl2.FitInfo
ans = struct with fields:
          TerminationCode: 1
        TerminationStatus: "Relative tolerance on log-likelihood satisfied."
            NumIterations: 37
    NegativeLogLikelihood: 5.4466e+04
               Perplexity: 558.8685
                   Solver: "cgs"
                  History: [1x1 struct]

Compute the perplexity of the held-out test set.

[~,ppl2] = logp(mdl2,documentsTest)
ppl2 = 
808.6602

A lower perplexity suggests that the model may be better fit to the held-out test data.

Input Arguments

collapse all

Input LDA model, specified as an ldaModel object.

Input documents, specified as a tokenizedDocument array, a string array of words, or a cell array of character vectors. If documents is not a tokenizedDocument array, then it must be a row vector representing a single document, where each element is a word. To specify multiple documents, use a tokenizedDocument array.

Input bag-of-words or bag-of-n-grams model, specified as a bagOfWords object or a bagOfNgrams object. If bag is a bagOfNgrams object, then the function treats each n-gram as a single word.

Frequency counts of words, specified as a matrix of nonnegative integers. If you specify 'DocumentsIn' to be 'rows', then the value counts(i,j) corresponds to the number of times the jth word of the vocabulary appears in the ith document. Otherwise, the value counts(i,j) corresponds to the number of times the ith word of the vocabulary appears in the jth document.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'NumSamples',500 specifies to draw 500 samples for each document

Orientation of documents in the word count matrix, specified as the comma-separated pair consisting of 'DocumentsIn' and one of the following:

  • 'rows' – Input is a matrix of word counts with rows corresponding to documents.

  • 'columns' – Input is a transposed matrix of word counts with columns corresponding to documents.

This option only applies if you specify the input documents as a matrix of word counts.

Note

If you orient your word count matrix so that documents correspond to columns and specify 'DocumentsIn','columns', then you might experience a significant reduction in optimization-execution time.

Number of samples to draw for each document, specified as the comma-separated pair consisting of 'NumSamples' and a positive integer.

Example: 'NumSamples',500

Output Arguments

collapse all

Log-probabilities of the documents under the LDA model, returned as a numeric vector.

Perplexity of the documents calculated from the log-probabilities, returned as a positive scalar.

Algorithms

The logp uses the iterated pseudo-count method described in [1].

References

[1] Wallach, Hanna M., Iain Murray, Ruslan Salakhutdinov, and David Mimno. "Evaluation methods for topic models." In Proceedings of the 26th annual international conference on machine learning, pp. 1105–1112. ACM, 2009. Harvard

Version History

Introduced in R2017b

See Also

| | | | |

Topics