Main Content

insSensor

Inertial navigation system and GNSS/GPS simulation model

Since R2020b

expand all in page

Description

The insSensor System object™ models a device that fuses measurements from an inertial navigation system (INS) and global navigation satellite system (GNSS) such as a GPS, and outputs the fused measurements.

To output fused INS and GNSS measurements:

  1. Create the insSensor object and set its properties.

  2. Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

INS = insSensor
INS = insSensor(Name,Value)

Description

INS = insSensor returns a System object, INS, that models a device that outputs measurements from an INS and GNSS.

example

INS = insSensor(Name,Value) sets properties using one or more name-value pairs. Unspecified properties have default values. Enclose each property name in quotes.

example

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

Location of the sensor on the platform, in meters, specified as a three-element real-valued vector of the form [x y z]. The vector defines the offset of the sensor origin from the origin of the platform.

Tunable: Yes

Data Types: single | double

Accuracy of the roll measurement of the sensor body, in degrees, specified as a nonnegative real scalar.

Roll is the rotation around the x-axis of the sensor body. Roll noise is modeled as a white noise process. RollAccuracy sets the standard deviation of the roll measurement noise.

Tunable: Yes

Data Types: single | double

Accuracy of the pitch measurement of the sensor body, in degrees, specified as a nonnegative real scalar.

Pitch is the rotation around the y-axis of the sensor body. Pitch noise is modeled as a white noise process. PitchAccuracy defines the standard deviation of the pitch measurement noise.

Tunable: Yes

Data Types: single | double

Accuracy of the yaw measurement of the sensor body, in degrees, specified as a nonnegative real scalar.

Yaw is the rotation around the z-axis of the sensor body. Yaw noise is modeled as a white noise process. YawAccuracy defines the standard deviation of the yaw measurement noise.

Tunable: Yes

Data Types: single | double

Accuracy of the position measurement of the sensor body, in meters, specified as a nonnegative real scalar or a three-element real-valued vector. The elements of the vector set the accuracy of the x-, y-, and z-position measurements, respectively. If you specify PositionAccuracy as a scalar value, then the object sets the accuracy of all three positions to this value.

Position noise is modeled as a white noise process. PositionAccuracy defines the standard deviation of the position measurement noise.

Tunable: Yes

Data Types: single | double

Accuracy of the velocity measurement of the sensor body, in meters per second, specified as a nonnegative real scalar.

Velocity noise is modeled as a white noise process. VelocityAccuracy defines the standard deviation of the velocity measurement noise.

Tunable: Yes

Data Types: single | double

Accuracy of the acceleration measurement of the sensor body, in meters per second, specified as a nonnegative real scalar.

Acceleration noise is modeled as a white noise process. AccelerationAccuracy defines the standard deviation of the acceleration measurement noise.

Tunable: Yes

Data Types: single | double

Accuracy of the angular velocity measurement of the sensor body, in meters per second, specified as a nonnegative real scalar.

Angular velocity is modeled as a white noise process. AngularVelocityAccuracy defines the standard deviation of the acceleration measurement noise.

Tunable: Yes

Data Types: single | double

Enable input of simulation time, specified as a logical 0 (false) or 1 (true). Set this property to true to input the simulation time by using the simTime argument.

Tunable: No

Data Types: logical

Enable GNSS fix, specified as a logical 1 (true) or 0 (false). Set this property to false to simulate the loss of a GNSS receiver fix. When a GNSS receiver fix is lost, position measurements drift at a rate specified by the PositionErrorFactor property.

Tunable: Yes

Dependencies

To enable this property, set TimeInput to true.

Data Types: logical

Position error factor without GNSS fix, specified as a scalar or a 1-by-3 vector of scalars.

When the HasGNSSFix property is set to false, the position error grows at a quadratic rate due to constant bias in the accelerometer. The position error for a position component E(t) can be expressed as E(t) = 1/2αt2, where α is the position error factor for the corresponding component and t is the time since the GNSS fix is lost. While running, the object computes t based on the simTime input. The computed E(t) values for the x, y, and z components are added to the corresponding position components of the gTruth input.

Tunable: Yes

Dependencies

To enable this property, set TimeInput to true and HasGNSSFix to false.

Data Types: single | double

Random number source, specified as one of these options:

  • 'Global stream' –– Generate random numbers using the current global random number stream.

  • 'mt19937ar with seed' –– Generate random numbers using the mt19937ar algorithm, with the seed specified by the Seed property.

Data Types: char | string

Initial seed of the mt19937ar random number generator algorithm, specified as a nonnegative integer.

Dependencies

To enable this property, set RandomStream to 'mt19937ar with seed'.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Usage

Syntax

measurement = INS(gTruth)
measurement = INS(gTruth,simTime)

Description

measurement = INS(gTruth) models the data received from an INS sensor reading and GNSS sensor reading. The output measurement is based on the inertial ground-truth state of the sensor body, gTruth.

example

measurement = INS(gTruth,simTime) additionally specifies the time of simulation, simTime. To enable this syntax, set the TimeInput property to true.

Input Arguments

expand all

Inertial ground-truth state of sensor body, in local Cartesian coordinates, specified as a structure containing these fields:

FieldDescription
'Position'

Position, in meters, specified as a real, finite N-by-3 matrix of [x y z] vectors. N is the number of samples in the current frame.

'Velocity'

Velocity (v), in meters per second, specified as a real, finite N-by-3 matrix of [vx vy vz] vector. N is the number of samples in the current frame.

'Orientation'

Orientation with respect to the local Cartesian coordinate system, specified as one of these options:

  • N-element column vector of quaternion objects

  • 3-by-3-by-N array of rotation matrices

  • N-by-3 matrix of [xroll ypitch zyaw] angles in degrees

Each quaternion or rotation matrix is a frame rotation from the local Cartesian coordinate system to the current sensor body coordinate system. N is the number of samples in the current frame.

'Acceleration'

Acceleration (a), in meters per second squared, specified as a real, finite N-by-3 matrix of [ax ay az] vectors. N is the number of samples in the current frame.

'AngularVelocity'

Angular velocity (ω), in degrees per second squared, specified as a real, finite N-by-3 matrix of [ωx ωy ωz] vectors. N is the number of samples in the current frame.

The field values must be of type double or single.

The Position, Velocity, and Orientation fields are required. The other fields are optional.

Example: struct('Position',[0 0 0],'Velocity',[0 0 0],'Orientation',quaternion([1 0 0 0]))

Simulation time, in seconds, specified as a nonnegative real scalar.

Data Types: single | double

Output Arguments

expand all

Measurement of the sensor body motion, in local Cartesian coordinates, returned as a structure containing these fields:

FieldDescription
'Position'

Position, in meters, specified as a real, finite N-by-3 matrix of [x y z] vectors. N is the number of samples in the current frame.

'Velocity'

Velocity (v), in meters per second, specified as a real, finite N-by-3 matrix of [vx vy vz] vector. N is the number of samples in the current frame.

'Orientation'

Orientation with respect to the local Cartesian coordinate system, specified as one of these options:

  • N-element column vector of quaternion objects

  • 3-by-3-by-N array of rotation matrices

  • N-by-3 matrix of [xroll ypitch zyaw] angles in degrees

Each quaternion or rotation matrix is a frame rotation from the local Cartesian coordinate system to the current sensor body coordinate system. N is the number of samples in the current frame.

'Acceleration'

Acceleration (a), in meters per second squared, specified as a real, finite N-by-3 matrix of [ax ay az] vectors. N is the number of samples in the current frame.

'AngularVelocity'

Angular velocity (ω), in degrees per second squared, specified as a real, finite N-by-3 matrix of [ωx ωy ωz] vectors. N is the number of samples in the current frame.

The returned field values are of type double or single and are of the same type as the corresponding field values in the gTruth input.

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

expand all

perturbationsPerturbation defined on object
perturbApply perturbations to object
stepRun System object algorithm
cloneCreate duplicate System object
isLockedDetermine if System object is in use
resetReset internal states of System object
releaseRelease resources and allow changes to System object property values and input characteristics

Examples

collapse all

Open Live Script

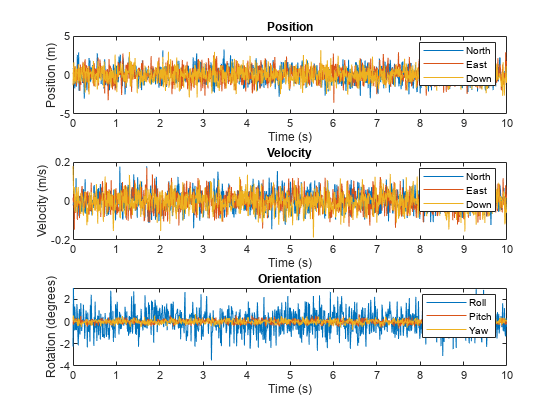
Create a motion structure that defines a stationary position at the local north-east-down (NED) origin. Because the platform is stationary, you need to define only a single sample. Assume the ground-truth motion is sampled for 10 seconds with a 100 Hz sample rate. Create a default insSensor System object™. Preallocate variables to hold output from the insSensor object.

Fs = 100;
duration = 10;
numSamples = Fs*duration;

motion = struct( ...
    'Position',zeros(1,3), ...
    'Velocity',zeros(1,3), ...
    'Orientation',ones(1,1,'quaternion'));

INS = insSensor;

positionMeasurements = zeros(numSamples,3);
velocityMeasurements = zeros(numSamples,3);
orientationMeasurements = zeros(numSamples,1,'quaternion');

In a loop, call INS with the stationary motion structure to return the position, velocity, and orientation measurements in the local NED coordinate system. Log the position, velocity, and orientation measurements.

for i = 1:numSamples
    
    measurements = INS(motion);
    
    positionMeasurements(i,:) = measurements.Position;
    velocityMeasurements(i,:) = measurements.Velocity;
    orientationMeasurements(i) = measurements.Orientation;
    
end

Convert the orientation from quaternions to Euler angles for visualization purposes. Plot the position, velocity, and orientation measurements over time.

orientationMeasurements = eulerd(orientationMeasurements,'ZYX','frame');

t = (0:(numSamples-1))/Fs;

subplot(3,1,1)
plot(t,positionMeasurements)
title('Position')
xlabel('Time (s)')
ylabel('Position (m)')
legend('North','East','Down')

subplot(3,1,2)
plot(t,velocityMeasurements)
title('Velocity')
xlabel('Time (s)')
ylabel('Velocity (m/s)')
legend('North','East','Down')

subplot(3,1,3)
plot(t,orientationMeasurements)
title('Orientation')
xlabel('Time (s)')
ylabel('Rotation (degrees)')
legend('Roll', 'Pitch', 'Yaw')

Figure contains 3 axes objects. Axes object 1 with title Position, xlabel Time (s), ylabel Position (m) contains 3 objects of type line. These objects represent North, East, Down. Axes object 2 with title Velocity, xlabel Time (s), ylabel Velocity (m/s) contains 3 objects of type line. These objects represent North, East, Down. Axes object 3 with title Orientation, xlabel Time (s), ylabel Rotation (degrees) contains 3 objects of type line. These objects represent Roll, Pitch, Yaw.

Open Live Script

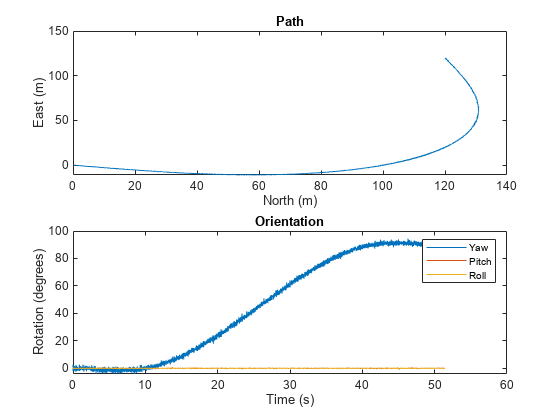
Generate INS measurements using the insSensor System object™. Use waypointTrajectory to generate the ground-truth path.

Specify a ground-truth orientation that begins with the sensor body x-axis aligned with North and ends with the sensor body x-axis aligned with East. Specify waypoints for an arc trajectory and a time-of-arrival vector for the corresponding waypoints. Use a 100 Hz sample rate. Create a waypointTrajectory System object with the waypoint constraints, and set SamplesPerFrame so that the entire trajectory is output with one call.

eulerAngles = [0,0,0; ...
               0,0,0; ...
               90,0,0; ...
               90,0,0];
orientation = quaternion(eulerAngles,'eulerd','ZYX','frame');

r = 20;
waypoints = [0,0,0; ...
             100,0,0; ...
             100+r,r,0; ...
             100+r,100+r,0];

toa = [0,10,10+(2*pi*r/4),20+(2*pi*r/4)];

Fs = 100;
numSamples = floor(Fs*toa(end));

path = waypointTrajectory('Waypoints',waypoints, ...
    'TimeOfArrival',toa, ...
    'Orientation',orientation, ...
    'SampleRate',Fs, ...
    'SamplesPerFrame',numSamples);

Create an insSensor System object to model receiving INS data. Set the PositionAccuracy to 0.1.

ins = insSensor('PositionAccuracy',0.1);

Call the waypoint trajectory object, path, to generate the ground-truth motion. Call the INS simulator, ins, with the ground-truth motion to generate INS measurements.

[motion.Position,motion.Orientation,motion.Velocity] = path();
insMeas = ins(motion);

Convert the orientation returned by ins to Euler angles in degrees for visualization purposes. Plot the full path and orientation over time.

orientationMeasurementEuler = eulerd(insMeas.Orientation,'ZYX','frame');

subplot(2,1,1)
plot(insMeas.Position(:,1),insMeas.Position(:,2));
title('Path')
xlabel('North (m)')
ylabel('East (m)')

subplot(2,1,2)
t = (0:(numSamples-1)).'/Fs;
plot(t,orientationMeasurementEuler(:,1), ...
     t,orientationMeasurementEuler(:,2), ...
     t,orientationMeasurementEuler(:,3));
title('Orientation')
legend('Yaw','Pitch','Roll')
xlabel('Time (s)')
ylabel('Rotation (degrees)')

Figure contains 2 axes objects. Axes object 1 with title Path, xlabel North (m), ylabel East (m) contains an object of type line. Axes object 2 with title Orientation, xlabel Time (s), ylabel Rotation (degrees) contains 3 objects of type line. These objects represent Yaw, Pitch, Roll.

Extended Capabilities

Version History

Introduced in R2020b

See Also

Objects

Objects