basisPursuit
Description
[
specifies options using one or more name-value arguments in addition to the input argument
in the previous syntax. For example, Xr,MSE,lambda] = basisPursuit(___,Name=Value)[Xr,MSE,lambda] =
basisPursuit(A,Y,RelTol=5e-2) sets a relative tolerance of
5e-2.
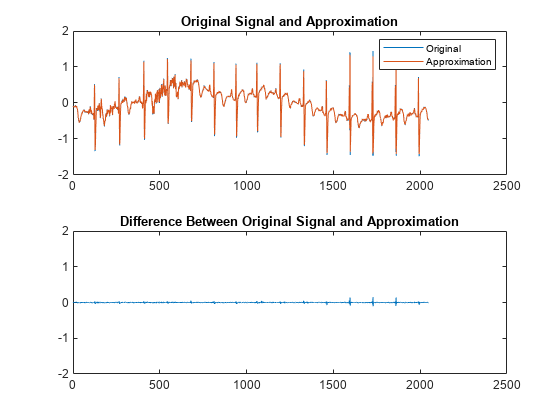
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Extended Capabilities
Version History
Introduced in R2022a