Main Content

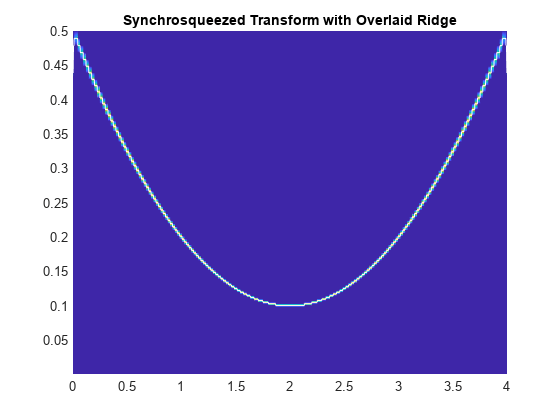
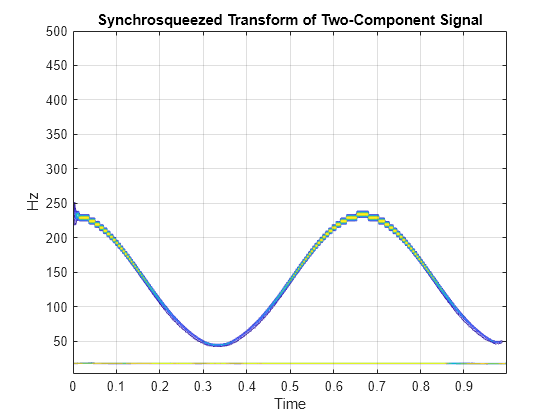
wsstridge

Time-frequency ridges from wavelet synchrosqueezing

collapse all in page

Syntax

fridge = wsstridge(sst)
[fridge,iridge] = wsstridge(sst)
[___] = wsstridge(sst,penalty)
[___] = wsstridge(___,f)
[___]= wsstridge(___,Name=Value)

Description

fridge = wsstridge(sst) extracts the maximum energy time-frequency ridge in cycles per sample from the wavelet synchrosqueezed transform, sst. The sst input is the output of wsst using the analytic Morlet wavelet. Each ridge is a separate signal mode.

If you used a wavelet other than the default Morlet wavelet ("amor") in wsst, or a nondefault VoicesPerOctave value in wsst, you can use the optional continuous wavelet transform (CWT) filter bank parameters output from wsst and input that to wsstridge using the FilterBankParameters name-value argument. Alternatively, you can output the frequencies f from wsst and use those directly in wsstridge.

[fridge,iridge] = wsstridge(sst) returns in iridge the row indices of sst. The row indices are the maximum time-frequency ridge at each sample. Use iridge to reconstruct the signal mode along a time-frequency ridge using iwsst.

example

[___] = wsstridge(sst,penalty) multiplies the squared distance between frequency bins by the penalty value. You can include any of the output arguments from previous syntaxes.

[___] = wsstridge(___,f) returns the maximum energy time-frequency ridge in cycles per unit time based on the f input frequency vector. f is the frequency output of wsst. The f input and fridge output have the same units.

[___]= wsstridge(___,Name=Value) returns the time-frequency ridge with additional options specified by one or more Name=Value arguments.

example

Examples

collapse all

Open Live Script

Obtain the wavelet synchrosqueezed transform of a quadratic chirp and extract the maximum time-frequency ridge, in fridge, and the associated row indices, in iridge.

Load the chirp signal and obtain its synchrosqueezed transform.

load quadchirp
[sst,f] = wsst(quadchirp);

Extract the maximum time-frequency ridge.

[fridge,iridge] = wsstridge(sst);

Plot the synchrosqueezed transform.

pcolor(tquad,f,abs(sst))
shading interp
title("Synchrosqueezed Transform")

Figure contains an axes object. The axes object with title Synchrosqueezed Transform contains an object of type surface.

Overlay the plot of the maximum energy frequency ridge.

hold on
plot(tquad,fridge,"w")
hold off
title("Synchrosqueezed Transform with Overlaid Ridge")

Figure contains an axes object. The axes object with title Synchrosqueezed Transform with Overlaid Ridge contains 2 objects of type surface, line.

Open Live Script

Extract the two highest energy modes from a multicomponent signal using two methods:

  • Use the frequency vector output of the wsst function.

  • Use the CWT filter bank parameters output of wsst.

Load a multicomponent signal. Obtain the CWT of the signal using the analytic Morlet wavelet.

load multicompsig
sig = sig1+sig2;

Method 1 — Frequency Vector

Obtain the wavelet synchrosqueezed transform of the signal. Also obtain the frequency vector output. Plot the output.

[sst,F] = wsst(sig,sampfreq);
contour(t,F,abs(sst))
xlabel("Time")
ylabel("Hz")
grid on
title("Synchrosqueezed Transform of Two-Component Signal")

Figure contains an axes object. The axes object with title Synchrosqueezed Transform of Two-Component Signal, xlabel Time, ylabel Hz contains an object of type contour.

Using a penalty of 10, extract the two highest energy modes and plot the result.

[fridge,iridge] = wsstridge(sst,10,F,NumRidges=2);
hold on
plot(t,fridge,"k",LineWidth=2)
hold off

Figure contains an axes object. The axes object with title Synchrosqueezed Transform of Two-Component Signal, xlabel Time, ylabel Hz contains 3 objects of type contour, line.

Method 2 — CWT Filter Bank Parameters

Obtain the wavelet synchrosqueezed transform of the signal. Also obtain the filter bank parameters. Plot the output.

[sst,~,fbparams] = wsst(sig,sampfreq);
contour(t,F,abs(sst))
xlabel("Time")
ylabel("Hz")
grid on
title("Synchrosqueezed Transform of Two-Component Signal")

Figure contains an axes object. The axes object with title Synchrosqueezed Transform of Two-Component Signal, xlabel Time, ylabel Hz contains an object of type contour.

Using a penalty of 10, extract the two highest energy modes using the filter bank parameters. Plot the result.

[fridge,iridge] = wsstridge(sst,10,NumRidges=2, ...
    FilterbankParameters=fbparams);
contour(t,F,abs(sst))
xlabel("Time")
ylabel("Hz")
grid on
title("Using Filter Bank Parameters")
hold on
plot(t,fridge,"k",LineWidth=2)
hold off

Figure contains an axes object. The axes object with title Using Filter Bank Parameters, xlabel Time, ylabel Hz contains 3 objects of type contour, line.

Input Arguments

collapse all

Synchrosqueezed transform, specified as a matrix. sst is a time-frequency matrix and is the output of wsst.

Data Types: single | double

Frequency bins scaling penalty, specified as a nonnegative scalar. This input penalizes changes in frequency by multiplying the penalty value by the squared distance between frequency bins. Use a penalty term when you extract multiple ridges, or when you have a single modulated component in additive noise. The penalty term prevents jumps in frequency that occur when the region of highest energy in the time-frequency plane changes abruptly.

Synchrosqueezed transform frequencies corresponding to the rows of the synchrosqueezed transform, which is the vector output of wsst. The number of elements in the frequency vector is equal to the number of rows in the sst input.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: NumRidges=3

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'NumRidges',3

Since R2024a

CWT filter bank parameters, specified as a structure array. The filter bank parameters are the optional structure array output fbparam of wsst. The wsstridge function uses the parameters to determine the frequencies used in the construction of the time-frequency ridges. Specifying FilterBankParameters is only valid if you do not use the input frequency vector, f.

Number of highest energy time-frequency ridges to extract, specified as a positive integer. If this integer is greater than 1, wsstridge iteratively determines the maximum energy time-frequency ridge by removing the previously computed ridges and the default or specified NumFrequencyBins on either side of each ridge bin.

Number of frequency bins to remove from synchrosqueezed transform sst when extracting multiple ridges, specified as a positive integer. This integer must be less than or equal to round(size(sst,1)/4). You can specify the number of frequency bins to remove only if you extract more than one ridge. After extracting the highest energy time-frequency ridge, wsstridge removes the sst values corresponding to the iridge indices at each time step. The energy is removed along the time-frequency ridge extended on both sides of the iridge index by the specified number of frequency bins. If the index of the extended time-frequency ridge exceeds the number of frequency bins at any time step, wsstridge truncates the removal region at the first or last frequency bin. To specify 'NumFrequencyBins', you must specify 'NumRidges'.

Output Arguments

collapse all

Time-frequency ridge frequencies, returned as a vector or matrix. The frequencies correspond to the time-frequency ridge at each time step. fridge is an N-by-nr matrix where N is the number of time samples (columns) in sst and nr is the number of ridges. The first column of the matrix contains the frequencies for the maximum energy time-frequency ridge in sst. Subsequent columns contain the frequencies for the time-frequency ridges in decreasing energy order. By default, fridge contains frequencies in cycles per sample.

Data Types: single | double

Time-frequency ridge row indices of sst, returned as a vector or matrix. The row indices in iridge correspond to the row index of the maximum time-frequency ridge for each sst column. iridge is an N-by-nr matrix where N is the number of time samples (columns) in sst, and nr is the number of ridges. The first column of the matrix contains the indices for the maximum energy time-frequency ridge in sst. Subsequent columns contain the indices for the time-frequency ridges in decreasing energy order.

Data Types: single | double

Algorithms

The function uses a penalized forward-backward greedy algorithm to extract the maximum-energy ridges from a time-frequency matrix. The algorithm finds the maximum time-frequency ridge by minimizing –ln A at each time point, where A is the absolute value of the matrix. Minimizing –ln A is equivalent to maximizing the value of A. The algorithm optionally constrains jumps in frequency with a penalty that is proportional to the distance between frequency bins.

The following example illustrates the time-frequency ridge algorithm using a penalty that is two times the distance between frequency bins. Specifically, the distance between the elements (j,k) and (m,n) is defined as (j-m)2. The time-frequency matrix has three frequency bins and three time steps. The matrix columns correspond to time steps, and the matrix rows correspond to frequency bins. The values in the second row represent a sine wave.

  1. Suppose you have the matrix:

    1   4   4
2   2   2
5   5   4

  2. Update the value for the (1,2) element as follows.

    1. Leave the values at the first time point unaltered. Begin the algorithm with the (1,2) element of the matrix, which presents the first frequency bin at the second time point. The bin value is 4. Penalize the values in the first column based on their distance from the (1,2) element. Applying the penalty to the first column produces

      original value + penalty × distance

1 + 2 × 0 =  1
2 + 2 × 1 =  4
5 + 2 × 4 = 13

       1   4
 4   2
13   5
      The minimum value of the first column is 1, which is in bin 1.

    2. Add the minimum value in column 1 to the current bin value, 4. The updated value for (1,2) becomes 5, which came from bin 1.

  3. Update the values for the remaining elements in column 2 as follows.

    Recompute the original column 1 values with the penalty factor using the same process as in Step 2a. Obtain the remaining second column values using the same process as in Step 2b. For example, when updating the (2,2) element, which has bin value 2, applying the penalty to the column yields

    original value + penalty × distance

1 + 2 × 1 =  3
2 + 2 × 0 =  2
5 + 2 × 1 =  7
    Add the minimum value, 2, to the current bin value. The updated value for (2,2) becomes 4. After updating the (3,2) element, the matrix is
    1   5(1)  4
2   4(2)  2
5   9(2)  4
    Only the second column has been updated. The subscripts indicate the index of the bin in the previous column from which a value came.

  4. Repeat Step 2 for the third column. But now the penalty is applied to the updated second column. For example, when updating the (1,3) element, the penalty is

    5 + 2 × 0 =  5
4 + 2 × 1 =  6
9 + 2 × 4 = 17
    The minimum value, 5, which is in the first bin, is added to the (1,3) bin value. After updating all the values in the third column, the final matrix is
    1   5(1)   9(1)
2   4(2)   6(2)
5   9(2)  10(2)

  5. Starting at the last column of the matrix, find the minimum value. Walk back in time through the matrix by going from the current bin to the origin of that bin at the previous time point. Keep track of the bin indices, which form the path composing the ridge. The algorithm smooths the transition by using the origin bin instead of the bin with the minimum value. For this example, the ridge indices are 2, 2, 2, which matches the energy path of the sine wave in row 2 of the matrix shown in Step 1.

If you are extracting multiple ridges, the algorithm removes the first ridge from the time-frequency matrix and repeats the process.

References

[1] Daubechies, I., J. Lu, and H.-T. Wu. "Synchrosqueezed wavelet transforms: an empirical mode decomposition-like tool." Applied and Computational Harmonic Analysis. Vol. 30, Number 2, 2011, pp. 243–261.

[2] Thakur, G., E. Brevdo, N. S. Fučkar, and H.-T. Wu. "The Synchrosqueezing algorithm for time-varying spectral analysis: Robustness properties and new paleoclimate applications." Signal Processing. Vol. 93, Number 4, 2013, pp. 1079–1094.

Version History

Introduced in R2016a

expand all

See Also

Functions

Objects

Topics