Main Content

Time-Varying Coherence

Open Live Script

Fourier-domain coherence is a well-established technique for measuring the linear correlation between two stationary processes as a function of frequency on a scale from 0 to 1. Because wavelets provide local information about data in time and scale (frequency), wavelet-based coherence allows you to measure time-varying correlation as a function of frequency. In other words, a coherence measure suitable for nonstationary processes.

To illustrate this, examine near-infrared spectroscopy (NIRS) data obtained in two human subjects. NIRS measures brain activity by exploiting the different absorption characteristics of oxygenated and deoxygenated hemoglobin. The recording site was the superior frontal cortex for both subjects and the data was sampled at 10 Hz. The data is taken from Cui, Bryant, & Reiss [1] and was kindly provided by the authors for this example.

In the experiment, the subjects alternatively cooperated and competed on a task. The period of the task was approximately 7.5 seconds.

load NIRSData
Fs = 10;
plot(tm,NIRSData(:,1))
hold on
plot(tm,NIRSData(:,2),"r")
hold off
legend("Subject 1","Subject 2",Location="NorthWest")
xlabel("Seconds")
title("NIRS Data")
grid on

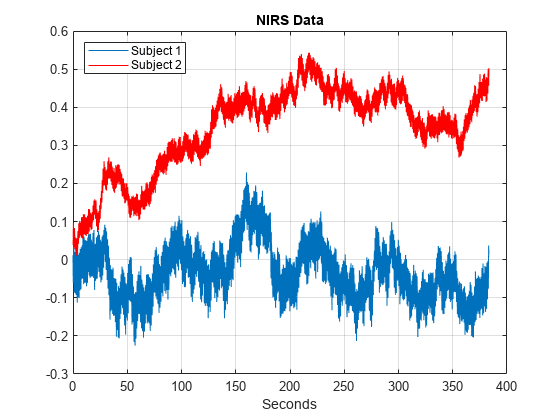
Figure contains an axes object. The axes object with title NIRS Data, xlabel Seconds contains 2 objects of type line. These objects represent Subject 1, Subject 2.

Examining the time-domain data, it is not clear what oscillations are present in the individual time series, or what oscillations are common to both data sets. Use wavelet analysis to answer both questions.

Obtain the wavelet coherence as a function of time and frequency. You can use the wcoherence function to output the wavelet coherence, cross-spectrum, scale-to- frequency, or scale-to-period conversions, as well as the cone of influence. In this example, the helper function helperPlotCoherence packages some useful commands for plotting the outputs of wcoherence.

figure
[wcoh,~,f,coi] = wcoherence(NIRSData(:,1),NIRSData(:,2),Fs, ...
    numscales=16);
helperPlotCoherence(wcoh,tm,f,coi,"Seconds","Hz");

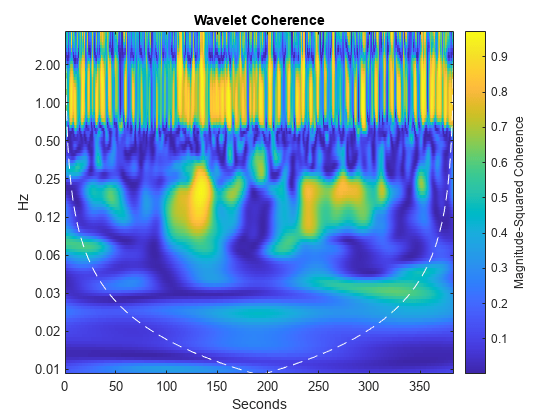
Figure contains an axes object. The axes object with title Wavelet Coherence, xlabel Seconds, ylabel Hz contains 2 objects of type image, line.

In the plot, you see a region of strong coherence throughout the data collection period around 1 Hz. This results from the cardiac rhythms of the two subjects. Additionally, you see regions of strong coherence around 0.13 Hz. This represents coherent oscillations in the subjects' brains induced by the task. If it is more natural to view the wavelet coherence in terms of periods rather than frequencies, you can input the sampling interval. With the sampling interval, wcoherence provides scale-to-period conversions.

[wcoh,~,P,coi] = wcoherence(NIRSData(:,1),NIRSData(:,2), ...
    seconds(1/10),numscales=16);
helperPlotCoherence(wcoh,tm,seconds(P),seconds(coi), ...
    "Time (secs)","Periods (Seconds)");

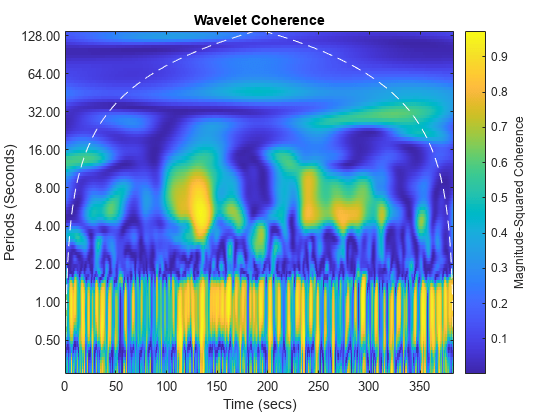
Figure contains an axes object. The axes object with title Wavelet Coherence, xlabel Time (secs), ylabel Periods (Seconds) contains 2 objects of type image, line.

Again, note the coherent oscillations corresponding to the subjects' cardiac activity occurring throughout the recordings with a period of approximately one second. The task-related activity is also apparent with a period of approximately 8 seconds. Consult Cui, Bryant, & Reiss [1] for a more detailed wavelet analysis of this data.

In summary, this example showed how to use wavelet coherence to look for time-localized coherent oscillatory behavior in two time series. For nonstationary signals, a measure of coherence that provides simultaneous time and frequency (period) information is often more useful.

References

[1] Cui, Xu, Daniel M. Bryant, and Allan L. Reiss. “NIRS-Based Hyperscanning Reveals Increased Interpersonal Coherence in Superior Frontal Cortex during Cooperation.” NeuroImage 59, no. 3 (February 2012): 2430–37. https://doi.org/10.1016/j.neuroimage.2011.09.003.

See Also

Related Topics