Reinforcement Learning for Trading
From the series: Machine Learning in Finance
Algorithmic stock trading is now the norm rather than the exception with the majority of trades being automated. Deep reinforcement learning is a promising area of research with the potential to mimic the decision-making of traders with years of experience on the trading floor.
Take a quick look into one potential application for deep reinforcement learning for trading using MATLAB®. Learn about an automated trading strategy that leverages reinforcement learning to decide when to hedge a European call option contract while accounting for transaction costs.
Published: 3 Jan 2020
In this video I will be talking about building an automated trader that is able to decide when to hedge a European call option contract in the presence of transaction costs using reinforcement learning.
Think of hedging as home insurance, but in finance we use hedging to reduce risk from stock price movement.
The amount of stocks traded at each time step is calculated using delta from the Black-Scholes formula. Therefore, if the call option is for 100 shares of MLB stock, and delta is 0.1, the trader needs to short 10 shares of MLB.
In a real-world scenario, where transaction costs exist, it becomes critical, while observing the market, to know when to hedge during the life of the option to have this tradeoff between trading costs and hedging risk.
Let’s see how we apply reinforcement learning in hedging.
The agent is observing the financial market inputs like the stock price, time to maturity, the option price, and the stock holdings and takes an action of whether to hedge or not. If the agent hedges, the new stock holdings are -51 calculated using delta. Therefore, the agent has sold 6 stocks resulting in $3 in transaction costs. If the agent doesn’t hedge, the holdings remain the same.
After one period, the stock price moves to $99.40. The agent observes a total profit and loss resulting from the change of the stock price, the change of the option price, transaction costs paid, and a reward related to the total profit and loss.
In reinforcement learning, the agent will learn by trial and error to maximize the cumulative reward by choosing when to hedge during the life of the option.
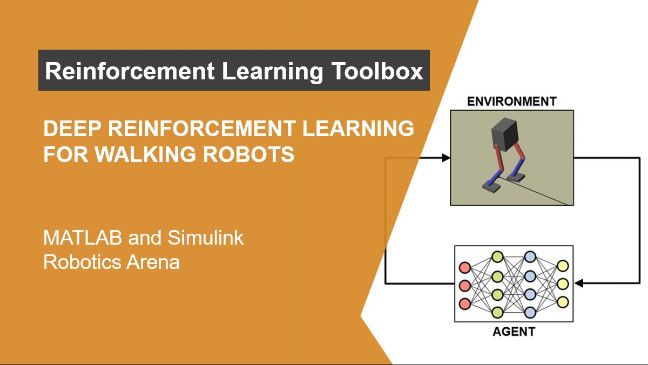
The RL setup is composed of an agent and an environment. The environment sends a state to the agent, which takes an action in response. The agent will evaluate its last action based on the reward it returned. The loop keeps going until the environment sends a terminal state, say the maturity of the option, which ends the episode. After each episode the agent will learn to take actions that maximize the cumulative reward.
MATLAB made it easier to set up the environment and design the reinforcement learning components.
The reset function returns the initial state of the environment. It is called at the beginning of each training episode.
The step function specifies how the environment advances to the next state based on which action the agent takes.
The observations include the stock price, time to maturity, and the agent’s stock holdings.
The action is whether to hedge or not.
The observations, actions, and reset and step functions form the environment.
The agent consists of a policy and a reinforcement learning algorithm. The policy is a mapping function between observations and action. It can be a neural network designed by specifying the layers, activation functions, and neurons.
The reinforcement learning algorithm continuously updates the policy parameters and will find an optimal policy that maximizes the cumulative reward.
We train the agent for an hour and we can see that the agent has learned to maximize the cumulative reward over time.
As a result, a trained agent outperformed a trader who used delta hedging and another who decided not to hedge at all.
We simulate a random stock path, and when all periods are hedged, the loss is $120. The agent hedged 38 periods and didn’t trade for 12 times and the loss is $55.
Thank you for watching.