Using a Photo for Full-Wave Antenna Analysis
By Vishwanath Iyer and Alex Taylor, MathWorks
Wireless applications such as NFC, RFID, and IoT system sensors benefit from low-cost antennas printed on plastic substrates. However, when the antenna is integrated into a system, there is often a mismatch between the data sheet specifications and the antenna's actual behavior and interaction with adjacent structures. In that case, you need to perform more advanced analysis to fully understand the antenna characteristics—and that requires an accurate EM model of the antenna model.
Obtaining a geometric model of a printed antenna from basic geometric shapes can be tedious, as printed antennas often have multiple meanders and other structures to increase the gain and bandwidth. An easier solution is to derive the model from a photograph—but how do you ensure that the photo provides sufficient detail? And how do you deal with optical distortions that can occur in images taken with a webcam or smart phone?
Two apps can help you address these issues. The Camera Calibrator app in Computer Vision Toolbox™ lets you calibrate a webcam to improve measurement accuracy. You can then use Image Segmenter app in Image Processing Toolbox™ to perform segmentation on the image and obtain the antenna boundaries.
Using an RFID tag as an example, this article presents a workflow for building and analyzing an antenna from a photo (Figure 1). It describes the steps to segment an image, find the geometric boundaries, calibrate the antenna size, and analyze the antenna using a full-wave method of moments (MoM) technique.
Figure 1. Workflow for building and analyzing an antenna from a photo.
The RFID Tag
Radio frequency identification (RFID) tags are typically used on boxes and pallets for inventory tracking. The tag consists of a radiating structure, the antenna, and a chip designed for operation over the frequency band. The antenna is typically narrowband, with an omnidirectional pattern in one of the two principal planes, and it has a complex impedance at resonance to ensure a good impedance match to the input of the chip. Our goal in this example is to confirm these port, surface, and field characteristics of the RFID tag antenna.
We begin by taking a photo of the tag against a high-color-contrast background. We use an inexpensive webcam and the webcam function to acquire images directly within MATLAB® (Figure 2).
c = webcam(); img = snapshot(c)
Figure 2. The photograph of the RFID tag taken against a high-contrast background.
To ensure accurate measurement of distances along the antenna boundary, we position the camera directly over the antenna so that all points along the surface of the antenna are approximately the same distance from the camera.
Calibrating the Camera Using the Camera Calibrator App
Camera calibration is an important part of any distance measurement workflow, particularly when you are working with cameras with low-quality lens optics, as in this example.
With the Camera Calibrator app in Computer Vision Toolbox, we can calibrate the webcam by simply taking photos of a checkerboard calibration pattern at different orientations and distances from the camera (Figure 3).
Figure 3. Sequence of photographs of a checkerboard calibration pattern loaded into the Camera Calibrator app.
Once we've acquired a set of calibration images from the webcam, we can compute the camera parameters using the Calibrate button in the app toolstrip (Figure 4).
Figure 4. The Camera Calibrator app toolstrip.
We export these camera parameters from the app as a cameraParameters object. To remove the effect of lens distortion from an image acquired with a given camera, we use the cameraParameters of a camera, which model the lens distortion of a camera, together with the undistortImage function in Computer Vision Toolbox. The initial image and the undistorted image are shown in Figure 5.
undistortedImage = undistortImage(img,webcamParameters);
Figure 5. Top: the original webcam image. Bottom: the undistorted image obtained from the Camera Calibrator app.
The radial lens distortion present in the original image is due to physical imperfections in the optics of the camera lens. Near the focal center, where the antenna is, the effect of radial lens distortion is difficult to see. As you move to the edges of the image, the effect is most pronounced. The bowing around the upper and lower edges in the undistorted image reflects correction of lens distortion.
Segmenting the Image Using the Image Segmenter App
The Image Segmenter app includes a variety of algorithms that can be used in different combinations to explore the best way to segment objects. In this example, we'll use graph cut segmentation and an iterative energy minimization algorithm known as active contours and snakes.
Using the Graph Cut feature in the Image Segmenter app, we can segment the image based on color features, making “scribbles” to mark regions that lie in the foreground and background (red and green lines in Figure 6).
Figure 6. Foreground and background regions identified by making "scribbles" within the Image Segmenter app.
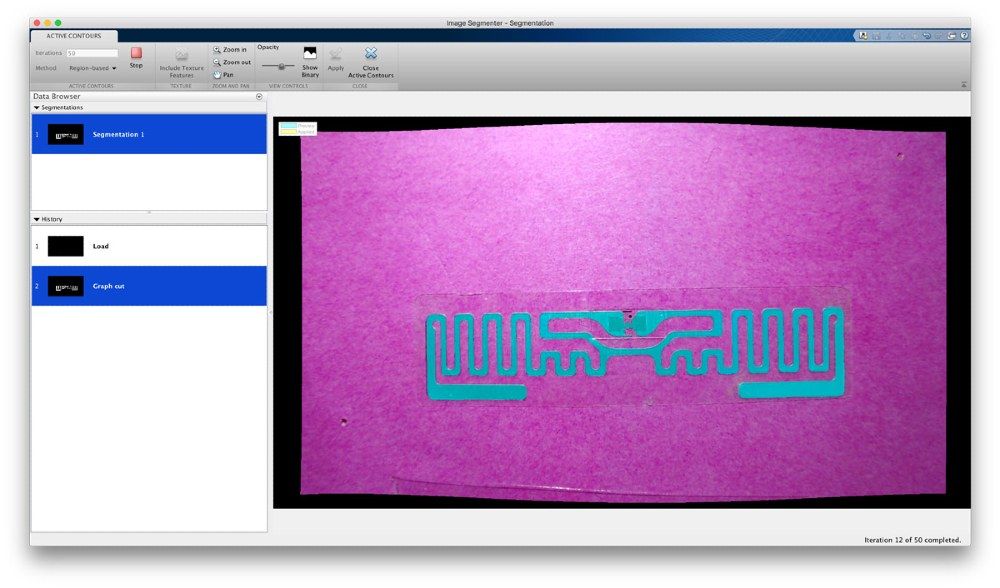
After obtaining an initial segmentation using the graph cut algorithm, we refine the segmentation using the active contour algorithm. The segmentation boundary that we obtained from the graph cut looks accurate. However, it has some small, jagged imperfections that we would like to refine.
Active contour is a good choice for the next step in our segmentation for two reasons. First, the algorithm starts from an input image and a segmentation mask and attempts to iteratively refine the mask so that it matches the boundary of the original image more closely. Second, one term in the active contour objective function being optimized describes the smoothness of the boundary in the segmentation mask, producing a segmentation with smoother borders (Figure 7).
Figure 7. Using the active contours postprocessing algorithm on the initial segmentation result from the graph-cut algorithm.
Having obtained an accurate segmentation mask, we export it from the Image Segmenter app into the MATLAB workspace (Figure 8).
Figure 8. Using the export button in the Image Segmenter app to export the mask to the workspace.
Performing Full-Wave Analysis
To perform full-wave analysis on this structure, we first need to convert the pixel space representation of the boundary to a Cartesian space representation. To do this we extract the maximum and minimum pixel indices in the x, y dimensions and convert them to (x,y) coordinates based on the length and width of the tag. Segmentation can produce a large number of points on the boundary: the RFID image boundary has approximately 11,000 points. An unintended consequence of this high-fidelity representation could be a very large mesh. To reduce the number of points on the boundary, we downsample it by a factor of 20. This downsample factor will still represent the boundary details accurately based on a simple visual inspection. The original boundary and the downsampled version are shown in Figures 9 and 10.
Figure 9. Boundary points obtained by scaling the points based on the tag dimensions.
Figure 10. Downsampled boundary.
There are two distinct sets of boundaries in this model: the outer boundary of the antenna and an inner boundary. This inner boundary must be removed so that the model accurately represents the topology of the antenna in the initial photo. We do this by loading the boundaries into the polygon objects in Antenna Toolbox™ and applying the Boolean subtract operation between them. We then center the geometry around the coordinate system origin and define the feed location for the antenna and a feed width. The resulting antenna is shown in Figure 11. In the following code segment, the two boundaries are stored in the variable BpD as a cell array.
outerPoly = antenna.Polygon;
outerPoly.Vertices = BpD{1};
innerPoly = antenna.Polygon;
innerPoly.Vertices = BpD{2};
c = outerPoly - innerPoly;
c = translate(c,[-(max(outerPoly.Vertices(:,1))-L/2),-(max(outerPoly.Vertices(:,2))-W/2),0]);
figure
show(c)
title('RFID antenna geometry')
Figure 11. The geometry of the RFID antenna built from the boundary definitions and Boolean operations on the polygon shapes in Antenna Toolbox.
The feed region around the point (0.0mm,0.0mm) has some sharp transitions that are artifacts detected by the segmentation algorithm. We need to clean these up to minimize the mesh in this region. We do this by defining a rectangle and slicing off the sections of the geometry around the feed to create a clean gap (Figure 12).
gap = antenna.Rectangle('Length', 6e-3, 'Width', 2e-3, 'Center', [-5.5e-3 -1e-3]); c = c - gap; figure show(c) title('RFID antenna geometry with gap across feed region')
Figure 12. The RFID antenna geometry with the feed region cleaned up by creating a gap.
We then define a feed strip across this gap to apply the excitation voltage. The antenna model with the feed fully specified is shown in Figure 13.
Figure 13. The RFID antenna model created with pcbStack. The feed region is defined using a rectangular strip.
After defining the overall boundary of the antenna, we specify two layers: the antenna geometry on top and a dielectric layer underneath. For this model, since the dielectric material is very thin, the initial analysis is executed by assuming the antenna is in free space. This allows us to do a first-pass analysis on the tag fairly rapidly since we do not need to construct a mesh for the dielectric material. The presence of the dielectric will have a small change in the overall behavior of the tag as long as the material is low loss and low relative permittivity (εr<2). Finally, we specify the feed location as a triple consisting of [x,y,layerNumber]. The layerNumber is an integer indicating the layer on which the feed exists. Since this is an internal port for a balanced antenna, a single number is sufficient to fully specify the feed point.
feed = antenna.Rectangle('Length', 0.25e-3, 'Width', 3.0e-3, 'Center', [-5.5e-3, -1e-3]); cf = c + feed;
d = dielectric('Air'); p = pcbStack; p.Name = 'RFID-tag'; p.BoardShape = antenna.Rectangle('Length',22e-3,'Width',80e-3); p.Layers = {cf,d}; p.FeedLocations = [-5.5e-3, -1e-3, 1]; p.FeedDiameter = 0.5*0.25e-3; figure show(p) view(0,90)
The antenna is now ready for analysis.
Analyzing the Antenna
We begin by performing an impedance analysis to determine the port characteristics of the antenna over a coarsely sampled frequency range. To do so, use the impedance function with a pair of inputs, namely the antenna and the frequency. The RFID tag is expected to operate in the UHF band, between 800 and 900 MHz. The analysis frequency range will extend slightly beyond 900 MHz. Any analysis will result in an automatic meshing of the geometry at the highest frequency chosen in the range. This mesh is then passed into the solver, which identifies the feed location and the corresponding feeding edge to apply a 1V excitation. The interaction matrix between the RWG basis functions (pairs of triangles) is calculated and the unknowns in the form of the currents on the surface are solved for.
f_coarse = linspace(0.8e9,0.95e9,21); figure impedance(p, f_coarse)
The tag is inductive and has a good resistive component at approximately 857 MHz (Figure 14). Moreover, the reactance shows the classic parallel resonance curve around that frequency.
Figure 14. Impedance of the RFID antenna. The inductive nature of the tag is evident from the reactance curve (red).
Figure 15 shows the mesh generated for this analysis.
figure mesh(p)
Figure 15. The mesh generated for analysis; the highest frequency in the frequency range was chosen for generating the mesh.
Typically, the input impedance of the chip would be complex, to match to the tag. We use the Load property on the antenna to cancel the inductive component. Since the reactance is about 200 Ω, we create a load with reactance of -200 Ω and add it to the antenna model. With the load in place at the feed, the inductive part of the reactance should be canceled at 857 MHz. We confirm this by analyzing the impedance over a finer frequency range. The reactance at 857 MHz is approximately 0 Ω (Figure 16).
X = -1i*200; zl = lumpedElement; zl.Impedance = X; p.Load = zl; f_fine = linspace(0.8e9,0.95e9,51); figure impedance(p, f_fine)
Figure 16. Impedance of the tag after the inclusion of a capacitive reactance at the feed. The reactance cancellation is observed with a zero crossing in the reactance curve.
The current distribution shows a strong response at 857 MHz, with significant current being developed on the surface of the antenna (Figure 17). We use the colorbar to interactively adjust the current density range.
figure current(p,857e6) view(0,90)
Figure 17. Current distribution of the capacitively loaded RFID tag at the resonance frequency of 857 MHz.
RFID tags typically have an omnidirectional far-field pattern in one plane. To confirm this, we can visualize the far-field radiation pattern of the tag. The tag has a gain of approximately 2 dBi at 857 MHz. As Figure 18 shows, the maximum directivity occurs in elevation at an azimuth of 0 degrees and nulls along the axis with the maximum dimensions of the tag. This response of the antenna is similar to that of a simple half-wavelength dipole antenna resting on the xy plane with the same orientation as the tag.
figure pattern(p,857e6)
Figure 18. Directivity pattern of the capacitively loaded RFID tag at the resonance frequency of 857 MHz.
Summary and Next Steps
This example demonstrated a procedure for identifying the antenna boundary from a photograph and converting it into a geometric model of the antenna for full-wave analysis. After removing optical lens distortions in the image using apps from Computer Vision Toolbox and Image Processing Toolbox, we built an antenna model and analyzed it in Antenna Toolbox using a full-wave method of moments–based solver. The analysis confirmed the parallel resonance behavior of the RFID tag and its inductive nature. The far-field radiation pattern follows that of a half-wavelength dipole and is omnidirectional in the elevation plane.
The analysis results can be used in a variety of ways. For example, the frequency-dependent impedance data can be used in an RF system simulation, and the radiation pattern can be used in an array-level simulation.
Published 2018
