comm.PNSequence

Generate a pseudonoise (PN) sequence

Description

The comm.PNSequence System object™ generates a sequence of pseudorandom binary numbers using a linear-feedback shift register (LFSR). This object implements LFSR using a simple shift register generator (SSRG, or Fibonacci) configuration. Pseudonoise sequences are typically used for pseudorandom scrambling and in direct-sequence spread-spectrum systems.

To generate a PN sequence:

Create the comm.PNSequence object and set its properties.
Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

pnSequence = comm.PNSequence

pnSequence = comm.PNSequence(Name,Value)

Description

pnSequence = comm.PNSequence creates a pseudonoise (PN) sequence generator System object. This object generates a sequence of pseudorandom binary numbers using a linear-feedback shift register (LFSR).

pnSequence = comm.PNSequence(Name,Value) sets properties using one or more name-value pairs. Enclose each property name in quotes. For example, 'Mask',1 specifies a one sample offset of the output sequence from the starting point.

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

`Polynomial` — Generator polynomial
`'z^6 + z + 1'` (default) | character vector | string scalar | binary row vector | integer vector

Generator polynomial that determines the feedback connections of the shift register, specified as one of these options:

Character vector or string scalar of a polynomial whose constant term is 1. For more information, see Representation of Polynomials in Communications Toolbox.
Binary-valued row vector that represents the coefficients of the polynomial in order of descending powers. The length of this vector must be N + 1, where N is the degree of the polynomial. The first and last entries must be 1, indicating the leading term with degree N and a constant term of 1.
Integer-valued row vector of elements that represent the exponents for the nonzero terms of the polynomial in order of descending powers. The last entry must be 0, indicating a constant term of 1.

For more information, see Simple Shift Register Generator and Polynomial Order and Shift Register Orientation.

Example: 'z^8 + z^2 + 1', [1 0 0 0 0 0 1 0 1], and [8 2 0] represent the same polynomial, p(z) = z⁸ + z² + 1.

Data Types: double | char

`InitialConditionsSource` — Source of initial conditions
`'Property'` (default) | `'Input port'`

Source of the initial conditions used for the shift register of the PN sequence, specified as one of these values:

'Property' — Specify PN sequence generator initial conditions by using the InitialConditions property.
'Input port' — Specify PN sequence generator initial conditions by using the initcond input argument.

Data Types: char

`InitialConditions` — Initial conditions of shift register
`[0 0 0 0 0 1]` (default) | binary scalar | binary vector

Initial conditions used for the shift register of the PN sequence generator when the simulation starts, specified as a binary-valued scalar or binary-valued vector.

If you set this property to a scalar, the initial value of all cells in the shift register are the specified scalar value.
If you set this property to a vector, each element of the vector corresponds to the initial value of the corresponding cell in the shift register. The length of the vector must equal the degree of the generator polynomial specified by the Polynomial property.

For more information, see Simple Shift Register Generator and Polynomial Order and Shift Register Orientation.

Note

For the object to generate a nonzero sequence, at least one element of the initial conditions for the first or second preferred PN sequence generator must be nonzero. Specifically, the initial state of at least one of the shift registers must be nonzero.

Dependencies

To enable this property, set InitialConditionsSource to 'Property'.

Data Types: double

`MaskSource` — Source of mask to shift PN sequence
`'Property'` (default) | `'Input port'`

Source of the mask that determines the shift of the PN sequence, specified as one of these:

'Property' — Specify the mask by using the Mask property.
'Input port' — Specify the mask by using the maskvec input argument.

Data Types: char

`Mask` — Mask to shift PN sequence
`0` (default) | integer scalar | binary vector

Mask that determines how the PN sequence is shifted from its starting point, specified as an integer scalar or a binary vector. The mask vector can be calculated using the shift2mask function.

When you set this property to an integer scalar, the value is the length of the shift. The object wraps shift values that are negative or greater than the length of the PN sequence.
When you set this property to a binary vector, its length must equal the degree of the generator polynomial specified by the Polynomial property.

For more information, see Shifting PN Sequence Starting Point and Polynomial Order and Shift Register Orientation.

Dependencies

To enable this property, set MaskSource to 'Property'.

`VariableSizeOutput` — Enable variable-size outputs
`false` (default) | `true`

Enable variable-size outputs, specified as a numeric or logical 0 (false) or 1 (true).

To enable variable-size outputs by using the outputsize input argument, set this property to true.The enabled input specifies the output size of the PN sequence. The input value must be less than or equal to the value of the MaximumOutputSize property.
When you set this property to false, the SamplesPerFrame property specifies the number of output samples.

`MaximumOutputSize` — Maximum output size
`[10 1]` (default) | vector of the form [m 1]

Maximum output frame size, specified as a vector of the form [m 1], where m is a positive integer. The first element of the vector indicates the maximum length of the output frame and the second element of the vector must be 1.

Example: [20 1] specifies a maximum frame output size of 20-by-1.

Dependencies

To enable this property, set VariableSizeOutput to true.

`SamplesPerFrame` — Number of samples output per frame
`1` (default) | positive integer

Number of samples output per frame, specified as a positive integer. If you set this property to a value of M, then the object outputs M samples of a PN sequence that has a period of N = 2ⁿ – 1, where n represents the degree of the generator polynomial that the Polynomial specifies.

If you set the BitPackedOutput property to false, the samples are bits from the PN sequence. If you set the BitPackedOutput property to true, then the output corresponds to SamplesPerFrame groups of bit-packed samples.

`ResetInputPort` — Enable generator reset input
`false` (default) | `true`

Enable the generator reset input, specified as a numeric or logical 0 (false) or 1 (true). To enable the ability to reset the sequence generator using the resetseq input argument, set this property to true. This input resets the states of the PN sequence generator to the initial conditions specified in the InitialConditions property. For more information, see Resetting a Signal.

Dependencies

To enable this property, set InitialConditionsSource to 'Property'.

`BitPackedOutput` — Output bit-packed words
`false` (default) | `true`

Option to output bit-packed words, specified as false or true. Set this property to true to enable bit-packed outputs.

When BitPackedOutput is true, the object outputs a column vector of length M, which contains most-significant-bit (MSB) first integer representations of bit words of length P. M is the number of samples per frame specified in the SamplesPerFrame property. P is the size of the bit-packed words specified in the NumPackedBits property.

Note

The first bit from the left in the bit-packed word contains the most significant bit for the integer representation.

`NumPackedBits` — Number of bits per bit-packed word
`8` (default) | integer in the range [1, 32]

Number of bits packed into each output data word, specified as an integer in the range [1, 32].

Dependencies

To enable this property, set BitPackedOutput to true.

`SignedOutput` — Output signed bit-packed words
`false` (default) | `true`

Set this property to true to obtain signed, bit-packed, output words. In this case, a 1 in the most significant bit (sign bit) indicates a negative value. The property indicates negative numbers in a two's complement format.

Dependencies

To enable this property, set BitPackedOutput to true.

`OutputDataType` — Data type of output
`'double'` (default) | `'logical'` | `'Smallest unsigned integer'` | `'Smallest integer'`

Output data type, specified as one of these values:

When BitPackedOutput is set to false, OutputDataType can be 'double', 'logical', or 'Smallest unsigned integer'.
When BitPackedOutput is set to true, OutputDataType can be 'double' or 'Smallest integer'.

Note

You must have a Fixed-Point Designer™ user license to use this property in 'Smallest unsigned integer' or 'Smallest integer' mode.

Dependencies

The valid settings for this property depend on the setting of the BitPackedOutput property.

Usage

Syntax

outSequence = pnSequence()

outSequence = pnSequence(initcond)

outSequence = pnSequence(maskvec)

outSequence = pnSequence(outputsize)

outSequence = pnSequence(resetseq)

outSequence = pnSequence(initcond,maskvec,outputsize)

outSequence = pnSequence(maskvec,outputsize,resetseq)

Description

outSequence = pnSequence() outputs a frame of the PN sequence in a column vector based on the configured object.

example

outSequence = pnSequence(initcond) uses initcond as the initial conditions for the PN sequence of the linear-feedback shift register.

To enable this syntax, set the InitialConditionsSource property to 'Input port'.

outSequence = pnSequence(maskvec) uses the maskvec input to specify the mask vector that determines how the PN sequence is shifted from its starting point.

To enable this syntax, set the MaskSource property to 'Input port'.

outSequence = pnSequence(outputsize) uses outputsize as the output size.

To enable this syntax, set the VariableSizeOutput property to true.

outSequence = pnSequence(resetseq) uses resetseq as the reset signal.

To enable this syntax, set the InitialConditionsSource property to 'Property' and the ResetInputPort property to true.

outSequence = pnSequence(initcond,maskvec,outputsize)

To enable this syntax, set the InitialConditionsSource property to 'Input port', the ResetInputPort property to false, the MaskSource property to 'Input port', and the VariableSizeOutput property to true.

outSequence = pnSequence(maskvec,outputsize,resetseq)

To enable this syntax, set the InitialConditionsSource property to 'Property', the MaskSource property to 'Input port', the VariableSizeOutput property to true, the ResetInputPort property to true.

Input Arguments

expand all

`initcond` — Initial register conditions used for shift register
binary-valued scalar | binary-valued vector

Initial conditions used for the shift register when the simulation starts, specified as a binary-valued scalar or binary-valued vector.

If you set this property to a scalar, the initial value of all cells in the shift register are the specified scalar value.
If you set this input to a vector, each element of the vector corresponds to the initial value of the corresponding cell in the shift register. The length of the vector must equal the degree of the generator polynomial specified by the Polynomial property.

Note

For the object to generate a nonzero sequence, at least one element of the initial condition for the PN sequence generator must be nonzero. Specifically, the initial state of at least one of the shift registers must be nonzero.

Example: outSequence = pnSequence([1 1 0]) corresponds to possible initial register states for a PN sequence generator specified by a generator polynomial of degree 3.

This object accepts variable-size inputs. After the object is locked, you can change the size of each input channel, but you cannot change the number of channels. For more information, see Variable-Size Signal Support with System Objects.

Dependencies

To use the syntax with this input, set InitialConditionsSource to 'Input port'.

Data Types: double

`maskvec` — Mask vector
binary vector

Mask that determines how the PN sequence is shifted from its starting point, specified as a binary vector. The length of the vector must equal the degree of the Polynomial property.

Dependencies

To use the syntax with this input, set MaskSource to 'Input port'.

`outputsize` — Length of output sequence
nonnegative integer | vector of the form [n 1]

Length of output sequence, specified as a nonnegative integer, n, or a vector of the form [n 1], where n is a positive integer. The first element of the vector indicates the length of the output frame and the second element of the vector must be 1.

The scalar or the first element of the row vector must be less than or equal to the first element of the MaximumOutputSize property value.

Dependencies

To enable this syntax with this input, set the VariableSizeOutput property to 'true'.

`resetseq` — Reset PN sequence generator
scalar | column vector

Reset sequence generator, specified as a scalar or a column vector with length equal to the number of samples per frame specified by the SamplesPerFrame property.

When you specify this input as a nonzero scalar, the object resets to the specified initial conditions and then generates a new output frame.
When you specify this input as a column vector, the object resets to the specified initial conditions at each sample in the output frame that aligns with a nonzero value in the reset vector.

For more information, see Resetting a Signal.

Dependencies

To enable this syntax with this input, set the InitialConditionsSource property to 'Property' and the ResetInputPort property to true.

Output Arguments

expand all

`outSequence` — PN Sequence
column vector

PN sequence generated by the object, returned as a column vector.

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

expand all

Common to All System Objects

`step`	Run System object algorithm
`release`	Release resources and allow changes to System object property values and input characteristics
`reset`	Reset internal states of System object

Examples

collapse all

Configuring a PN Sequence Generator

Open Live Script

When configuring a PN sequence generator System object™, you have options regarding how to express the polynomial and the mask. This figure defines a PN sequence generator with a generator polynomial $p (z) = z^{6} + z + 1$ and a mask $m (z) = z^{5} + z^{4} + z^{2} + 1$ . The example shows a few of the formatting options available to define the generator polynomial and the mask when you configure the PN sequence generator in this figure.

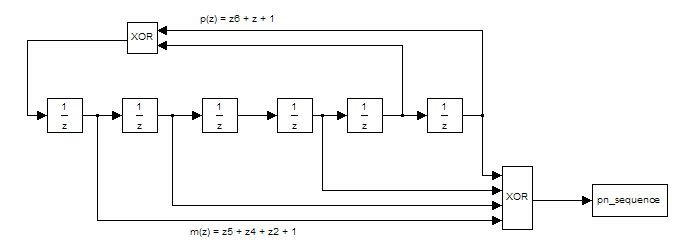
You can input the polynomial exponents of z for the nonzero terms of the polynomial in descending order of powers and the mask as a binary vector.

pnseq1 = comm.PNSequence('Polynomial',[6 1 0], ...
    'Mask',[1 1 0 1 0 1],'SamplesPerFrame',20)

pnseq1 = 
  comm.PNSequence with properties:

                 Polynomial: [6 1 0]
    InitialConditionsSource: 'Property'
          InitialConditions: [0 0 0 0 0 1]
                 MaskSource: 'Property'
                       Mask: [1 1 0 1 0 1]
         VariableSizeOutput: false
            SamplesPerFrame: 20
             ResetInputPort: false
            BitPackedOutput: false
             OutputDataType: 'double'

You can input the polynomial exponents as a binary-valued row vector that represents the coefficients of the polynomial in order of descending powers.

pnseq2 = comm.PNSequence('Polynomial',[1 0 0 0 0 1 1], ...
    'Mask',[1 1 0 1 0 1],'SamplesPerFrame',20)

pnseq2 = 
  comm.PNSequence with properties:

                 Polynomial: [1 0 0 0 0 1 1]
    InitialConditionsSource: 'Property'
          InitialConditions: [0 0 0 0 0 1]
                 MaskSource: 'Property'
                       Mask: [1 1 0 1 0 1]
         VariableSizeOutput: false
            SamplesPerFrame: 20
             ResetInputPort: false
            BitPackedOutput: false
             OutputDataType: 'double'

You can also define the mask as a scalar value using the mask2shift function.

mask2shift ([1 0 0 0 0 1 1],[1 1 0 1 0 1])

ans = 
22

pnseq3 = comm.PNSequence('Polynomial',[1 0 0 0 0 1 1], ...
    'Mask',22,'SamplesPerFrame',20)

pnseq3 = 
  comm.PNSequence with properties:

                 Polynomial: [1 0 0 0 0 1 1]
    InitialConditionsSource: 'Property'
          InitialConditions: [0 0 0 0 0 1]
                 MaskSource: 'Property'
                       Mask: 22
         VariableSizeOutput: false
            SamplesPerFrame: 20
             ResetInputPort: false
            BitPackedOutput: false
             OutputDataType: 'double'

Use each PN sequence object to generate a frame of 20 samples and compare the generated sequences.

out_1 = pnseq1();
out_2 = pnseq2();
out_3 = pnseq3();
isequal(out_1,out_2)

ans = logical
   1

isequal(out_1,out_3)

ans = logical
   1

Generate Maximal Length PN Sequences

Open Live Script

Generate a 14-sample frame of a maximal length PN sequence given generator polynomial, $x^{3} + x^{2} + 1$ .

Generate PN sequence data by using the comm.PNSequence object. The sequence repeats itself as it contains 14 samples while the maximal sequence length is only 7 samples ( $2^{3} - 1$ ).

pnSequence = comm.PNSequence('Polynomial',[3 2 0], ...
    'SamplesPerFrame',14,'InitialConditions',[0 0 1]);
x1 = pnSequence();
[x1(1:7) x1(8:14)]

Create another maximal length sequence based on the generator polynomial, $x^{4} + x + 1$ . As it is a fourth order polynomial, the sequence repeats itself after 15 samples ( $2^{4} - 1$ ).

pnSequence2 = comm.PNSequence('Polynomial','x^4+x+1', ...
    'InitialConditions',[0 0 0 1],'SamplesPerFrame',30);
x2 = pnSequence2();
[x2(1:15) x2(16:30)]

Generate Galois Linear-Feedback Shift Register Output

Open Live Script

The comm.PNSequence System object implements a linear-feedback shift register (LFSR) using a simple shift register generator (SSRG, or Fibonacci configuration). This configuration differs from the modular shift register generator (MSRG, or Galois configuration) by a phase difference, that can be determined empirically from the System object.

This phase difference can be specified as the Mask parameter for the comm.PNSequence System object to generate the equivalent MSRG configuration output. The block diagram represents the implementation of a 5-bit LFSR in the Galois (MSRG) configuration.

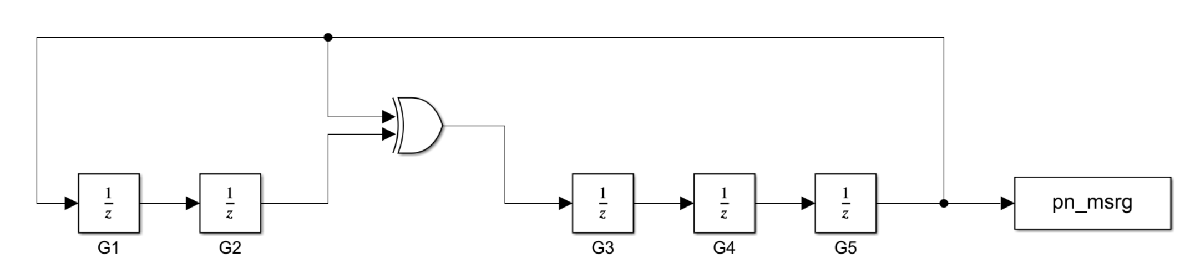
Load the file GaloisLFSR. The file contains the following variables that define the properties and output PN sequence of the 5-bit Galois LFSR:

polyVec: Generator polynomial
polySize: Degree of the generator polynomial
initStates: Initial conditions of the shift register
maskVar: Mask to shift the PN sequence
pn_msrg: Output PN sequence of maximal length, from the 5-bit Galois LFSR

load GaloisLFSR

Generate PN sequence data by using the comm.PNSequence object with the same set of properties used to implement the 5-bit Galois LFSR. Compare this PN sequence with the output of the 5-bit Galois LFSR. The two sequences differ by a phase shift.

pnSequence = comm.PNSequence( ...
    'Polynomial',polyVec, ...
    'InitialConditions',initStates,...
    'Mask',maskVar, ...
    'SamplesPerFrame',2^polySize-1);
pn = pnSequence();
isequal(pn,pn_msrg)

ans = logical
   0

Compute the phase shift between the two configurations. Set the value of the Mask property based on this phase shift.

for i = 1:length(pn)
    exp_pn = [pn(i:end);pn(1:(i-1))];
    if isequal(exp_pn,pn_msrg)
        break
    end
end
maskVar = i-1;

Generate PN sequence data by using the comm.PNSequence System object with the modified Mask property value. Compare this sequence with the output of the 5-bit Galois LFSR. The two sequences are now equal.

pnSequence_mod = comm.PNSequence( ...
    'Polynomial',polyVec, ...
    'InitialConditions',initStates,...
    'Mask',maskVar, ...
    'SamplesPerFrame',2^polySize-1);
pn_mod = pnSequence_mod();
isequal(pn_mod,pn_msrg)

ans = logical
   1

Additive Scrambling of Input Data

Open Live Script

Digital communications systems commonly use additive scrambling to randomize input data to aid in timing synchronization and power spectral requirements. The comm.Scrambler System object™ implements multiplicative scrambling but does not support additive scrambling. To perform additive scrambling you can use the comm.PNSequence System object. This example implements the additive scrambling specified in IEEE 802.11™ by scrambling input data with an output sequence generated by the comm.PNSequence System object. For a Simulink® model that implements a similar workflow, see the Additive Scrambling of Input Data in Simulink example.

This figure shows an additive scrambler, that uses the generator polynomial $x^{7} + x^{4} + 1$ , as specified in figure 17-7 of IEEE 802.11 Section 17.3.5.5 [1].

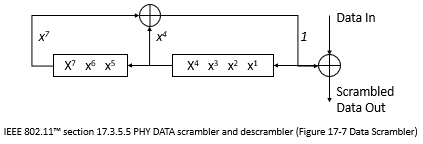
Comparing the shift register specified in 802.11 with the shift register implemented using a comm.PNSequence System object, note that the two shift register schematics are mirror images of each other. Therefore, when configuring the comm.PNSequence System object to implement an additive scrambler, you must reverse values for the generator polynomial, the initial states, and the mask output. To take the output of the register from the leading end, specify a shift value of 7.

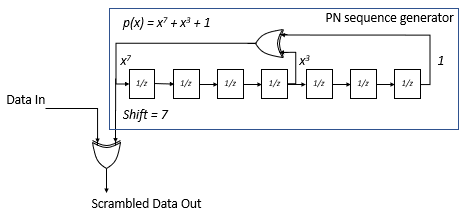
For more information about the 802.11 scrambler, see [1] and the wlanScramble (WLAN Toolbox) reference page.

Define variables for the generator polynomial, shift value for the output, an initial shift register state, a frame of input data, and a variable containing the 127-bit scrambler sequence specified in section 17.3.5.5 of the IEEE 802.11 standard. Create a PN sequence object that initializes the registers by using an input argument.

genPoly = 'x^7 + x^3 + 1';   % Generator polynomial
shift = 7;                   % Shift value for output
spf = 127;                   % Samples per frame
initState = [1 1 1 1 1 1 1]; % Initial shift register state
dataIn = randi([0 1],spf,1);
ieee802_11_scram_seq = logical([ ...
    0 0 0 0 1 1 1 0 1 1 1 1 0 0 1 0 1 1 0 0 1 ...
    0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 1 1 0 0 0 ...
    1 0 1 1 1 0 1 0 1 1 0 1 1 0 0 0 0 0 1 1 0 ...
    0 1 1 0 1 0 1 0 0 1 1 1 0 0 1 1 1 1 0 1 1 ...
    0 1 0 0 0 0 1 0 1 0 1 0 1 1 1 1 1 0 1 0 0 ...
    1 0 1 0 0 0 1 1 0 1 1 1 0 0 0 1 1 1 1 1 1 1])';

pnSeq = comm.PNSequence( ...
    Polynomial=genPoly, ...
    InitialConditionsSource="Input Port", ...
    Mask=shift, ...
    SamplesPerFrame=spf, ...
    OutputDataType="logical");
pnsequence = pnSeq(initState);

Compare the PN sequence object output to the IEEE 802.11 127-bit scrambler sequence to confirm the generated PN sequence matches the 802.11 specified sequence.

isequal(ieee802_11_scram_seq,pnsequence)

ans = logical
   1

Scramble input data according to the 802.11 specified additive scrambler by modulo-adding input data with the PN sequence output.

scrambledOut = xor(dataIn,pnSeq(initState));

Descramble the scrambled data by applying the same scrambler and initial conditions to the scrambled data.

descrambledData = xor(scrambledOut,pnSeq(initState));

Verify that the descrambled data matches the input data.

isequal(dataIn,descrambledData)

ans = logical
   1

Reference

[1] IEEE Std 802.11™-2020 (Revision of IEEE Std 802.11™-2016). "Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications." IEEE Standard for Information technology — Telecommunications and information exchange between systems. Local and metropolitan area networks — Specific requirements.

More About

expand all

Simple Shift Register Generator

A linear-feedback shift register (LFSR), implemented as a simple shift register generator (SSRG), is used to generate PN sequences. This type of shift register is also known as a Fibonacci implementation.

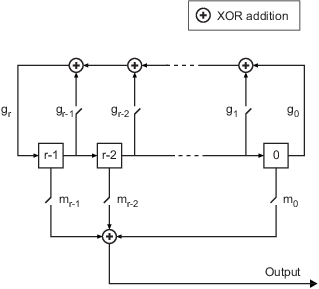
The polynomial g determines the feedback connections of the shift register. It is a primitive binary polynomial in z, g_rz^r+g_r–1z^r–1+g_r–2z^r–2+...+g₀. For the coefficient g_{k=0 to r}, the coefficient g_k is 1 if there is a connection from the kth register to the adder. The leading term, g_r, and the constant term, g₀, of the generator polynomial must be 1 because the polynomial must be primitive. At each time step, all r registers in the generator update their values according to the value of the incoming arrow to the shift register. The adders perform addition modulo 2. The output of the LFSR reflects the sum of all connections in the m mask vector.

g is specified by the Polynomial parameter.
The initial value of r is specified by the InitialConditions parameter.
m determines the shift of the PN sequence starting point and is specified by the Mask parameter or maskvec input argument.

This table indicates two sets of parameter values that correspond to the generator polynomial g(z) = z⁸ + z² + 1.

Quantity	Example 1	Example 2
g	`g1 = [1 0 0 0 0 0 1 0 1]`	`g2 = [8 2 0]`
Degree of generator polynomial	8, which is `length(g1)-1`	8
`InitialConditions`	`[1 0 0 0 0 0 1 0]`	`[1 0 0 0 0 0 1 0]`

For an example, see Generate Galois Linear-Feedback Shift Register Output.

Polynomial Order and Shift Register Orientation

The implementation orients shift registers from left to right with the generator polynomial (g), initial states, and mask output defined in descending order. Specifically g_rz^r+g_r–1z^r–1+g_r–2z^r–2+...+g₀.

When attempting to model and match results from literature, you must recognize whether your source uses the same convention or the mirror image of this convention and is defined in ascending order.

For an example, see Additive Scrambling of Input Data.

Shifting PN Sequence Starting Point

To shift the starting point of the PN sequence, specify the Mask property as:

An integer representing the length of the shift.

The default Mask setting of 0 corresponds to no shift. As illustrated in the LFSR shift register diagram in Simple Shift Register Generator, there is no shift when the only connection is along the arrow labeled m₀.

This table shows the shift that occurs when you set Mask to 0 versus a positive integer d.

	T = 0	T = 1	T = 2	...	T = d	T = d+1
Shift = 0	x₀	x₁	x₂	...	x_d	x_d+1
Shift = d	x_d	x_d+1	x_d+2	...	x_2d	x_2d+1

A binary vector whose length is equal to the degree of the generator polynomial. The LFSR shift register diagram in Simple Shift Register Generator shows Mask specified as a mask vector, m. The binary vector must have N elements, where N is the degree of the generator polynomial. To calculate the mask vector, use the shift2mask function.
The binary vector corresponds to a polynomial in z, m_r–1z^r–1 + m_r–2z^r–2 + ... + m₁z + m₀, of degree at most r – 1. The mask vector that corresponds to a shift of d is the vector that represents m(z) = z^d modulo g(z), where g(z) is the generator polynomial.
For example, if the degree of the generator polynomial is 4, then the mask vector that corresponds to d = 2 is [0 1 0 0], which represents the polynomial m(z) = z².

Resetting a Signal

To reset the PN generator sequence, you must first set the ResetInputPort property to true. Suppose that the system object generates a PN sequence of [1 0 0 1 1 0 1 1] when there is no reset. When the reset signal [0 0 0 1] is passed as an input argument to the object, the PN sequence is reset at the fourth bit, because the fourth bit of the reset signal is a 1.

Sequences of Maximum Length

To generate a maximum length sequence for a generator polynomial that has the degree r, set Polynomial to a value from the following table. The maximum sequence length is 2^r – 1.

r	Generator Polynomial	r	Generator Polynomial	r	Generator Polynomial	r	Generator Polynomial
2	`[2 1 0]`	15	`[15 14 0]`	28	`[28 25 0]`	41	`[41 3 0]`
3	`[3 2 0]`	16	`[16 15 13 4 0]`	29	`[29 27 0]`	42	`[42 23 22 1 0]`
4	`[4 3 0]`	17	`[17 14 0]`	30	`[30 29 28 7 0]`	43	`[43 6 4 3 0]`
5	`[5 3 0]`	18	`[18 11 0]`	31	`[31 28 0]`	44	`[44 6 5 2 0]`
6	`[6 5 0]`	19	`[19 18 17 14 0]`	32	`[32 31 30 10 0`	45	`[45 4 3 1 0]`
7	`[7 6 0]`	20	`[20 17 0]`	33	`[33 20 0]`	46	`[46 21 10 1 0]`
8	`[8 6 5 4 0]`	21	`[21 19 0]`	34	`[34 15 14 1 0]`	47	`[47 14 0]`
9	`[9 5 0]`	22	`[22 21 0]`	35	`[35 2 0]`	48	`[48 28 27 1 0]`
10	`[10 7 0]`	23	`[23 18 0]`	36	`[36 11 0]`	49	`[49 9 0]`
11	`[11 9 0]`	24	`[24 23 22 17 0]`	37	`[37 12 10 2 0]`	50	`[50 4 3 2 0]`
12	`[12 11 8 6 0]`	25	`[25 22 0]`	38	`[38 6 5 1 0]`	51	`[51 6 3 1 0]`
13	`[13 12 10 9 0]`	26	`[26 25 24 20 0]`	39	`[39 8 0]`	52	`[52 3 0]`
14	`[14 13 8 4 0]`	27	`[27 26 25 22 0]`	40	`[40 5 4 3 0]`	53	`[53 6 2 1 0]`

For more information about the shift register configurations that these polynomials represent, see Digital Communications by John Proakis [1].

References

[1] Proakis, John G. Digital Communications. 5th ed. New York: McGraw Hill, 2007.

[2] Lee, J. S., and L. E. Miller. CDMA Systems Engineering Handbook. Boston and London. Artech House, 1998.

[3] Golomb, S.W. Shift Register Sequences. Laguna Hills. Aegean Park Press, 1967.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

See System Objects in MATLAB Code Generation (MATLAB Coder).

Version History

Introduced in R2008a

comm.PNSequence

Description

Creation

Syntax

Description

Properties

Polynomial — Generator polynomial 'z^6 + z + 1' (default) | character vector | string scalar | binary row vector | integer vector

InitialConditionsSource — Source of initial conditions 'Property' (default) | 'Input port'

InitialConditions — Initial conditions of shift register [0 0 0 0 0 1] (default) | binary scalar | binary vector

Dependencies

MaskSource — Source of mask to shift PN sequence 'Property' (default) | 'Input port'

Mask — Mask to shift PN sequence 0 (default) | integer scalar | binary vector

Dependencies

VariableSizeOutput — Enable variable-size outputs false (default) | true

MaximumOutputSize — Maximum output size [10 1] (default) | vector of the form [m 1]

Dependencies

SamplesPerFrame — Number of samples output per frame 1 (default) | positive integer

ResetInputPort — Enable generator reset input false (default) | true

Dependencies

BitPackedOutput — Output bit-packed words false (default) | true

NumPackedBits — Number of bits per bit-packed word 8 (default) | integer in the range [1, 32]

Dependencies

SignedOutput — Output signed bit-packed words false (default) | true

Dependencies

OutputDataType — Data type of output 'double' (default) | 'logical' | 'Smallest unsigned integer' | 'Smallest integer'

Dependencies

Usage

Syntax

Description

Input Arguments

initcond — Initial register conditions used for shift register binary-valued scalar | binary-valued vector

Dependencies

maskvec — Mask vector binary vector

Dependencies

outputsize — Length of output sequence nonnegative integer | vector of the form [n 1]

Dependencies

resetseq — Reset PN sequence generator scalar | column vector

Dependencies

Output Arguments

outSequence — PN Sequence column vector

Object Functions

Common to All System Objects

Examples

Configuring a PN Sequence Generator

Generate Maximal Length PN Sequences

Generate Galois Linear-Feedback Shift Register Output

Additive Scrambling of Input Data

More About

Simple Shift Register Generator

Polynomial Order and Shift Register Orientation

Shifting PN Sequence Starting Point

Resetting a Signal

Sequences of Maximum Length

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.

Version History

See Also

Objects

Blocks

`Polynomial` — Generator polynomial
`'z^6 + z + 1'` (default) | character vector | string scalar | binary row vector | integer vector

`InitialConditionsSource` — Source of initial conditions
`'Property'` (default) | `'Input port'`

`InitialConditions` — Initial conditions of shift register
`[0 0 0 0 0 1]` (default) | binary scalar | binary vector

`MaskSource` — Source of mask to shift PN sequence
`'Property'` (default) | `'Input port'`

`Mask` — Mask to shift PN sequence
`0` (default) | integer scalar | binary vector

`VariableSizeOutput` — Enable variable-size outputs
`false` (default) | `true`

`MaximumOutputSize` — Maximum output size
`[10 1]` (default) | vector of the form [m 1]

`SamplesPerFrame` — Number of samples output per frame
`1` (default) | positive integer

`ResetInputPort` — Enable generator reset input
`false` (default) | `true`

`BitPackedOutput` — Output bit-packed words
`false` (default) | `true`

`NumPackedBits` — Number of bits per bit-packed word
`8` (default) | integer in the range [1, 32]

`SignedOutput` — Output signed bit-packed words
`false` (default) | `true`

`OutputDataType` — Data type of output
`'double'` (default) | `'logical'` | `'Smallest unsigned integer'` | `'Smallest integer'`

`initcond` — Initial register conditions used for shift register
binary-valued scalar | binary-valued vector

`maskvec` — Mask vector
binary vector

`outputsize` — Length of output sequence
nonnegative integer | vector of the form [n 1]

`resetseq` — Reset PN sequence generator
scalar | column vector

`outSequence` — PN Sequence
column vector

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.