Main Content

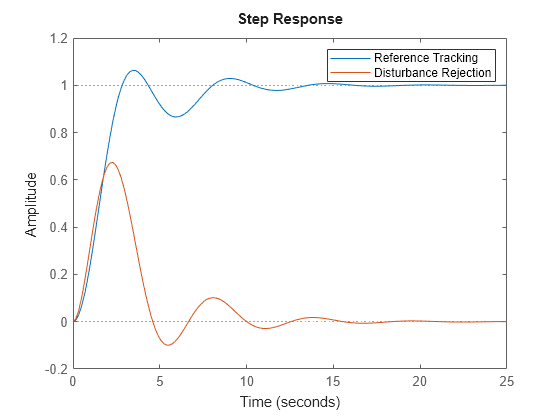
getPIDLoopResponse

Closed-loop and open-loop responses of systems with PID controllers

collapse all in page

Syntax

response = getPIDLoopResponse(C,G,looptype)

Description

response = getPIDLoopResponse(C,G,looptype) returns a response of the control loop formed by the PID controller C and the plant G. The function returns the closed-loop, open-loop, controller action, or disturbance response that you specify with the looptype argument. The function assumes the following control architecture.

  • When C is a pid or pidstd controller object (1-DOF controller):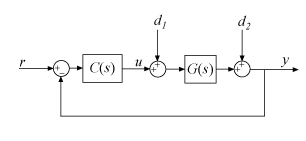

  • When C is a pid2 or pidstd2 controller object (2-DOF controller):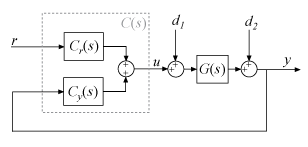

example

Examples

collapse all

Open Live Script

Design a PI controller for a SISO plant and examine its performance in reference tracking and disturbance rejection. For reference tracking, use the "closed-loop" response. For rejection of a load disturbance, use "input-disturbance".

G = tf(1,[1 1 1]);
C = pidtune(G,'PI');
Tref = getPIDLoopResponse(C,G,"closed-loop");
Tdist = getPIDLoopResponse(C,G,"input-disturbance");
step(Tref,Tdist)
legend("Reference Tracking","Disturbance Rejection")

MATLAB figure

Validate the tuned controller by comparing the extracted responses to your design requirements for settling time and overshoot.

Open Live Script

Design a two-degree-of-freedom (2-DOF) PID controller for a plant and examine its performance in reference tracking and disturbance rejection. For reference tracking, use the "closed-loop" response. For rejection of a load disturbance, use "input-disturbance".

G = tf(1,[1 0.5 0.1]);
w0 = 1.5;
C = pidtune(G,'PID2',w0);
Tref = getPIDLoopResponse(C,G,"closed-loop");
Tdist = getPIDLoopResponse(C,G,"input-disturbance");
step(Tref,Tdist)
legend("Reference Tracking","Disturbance Rejection")

MATLAB figure

Input Arguments

collapse all

PID controller, specified as a PID controller object (pid, pidstd, pid2, or pidstd2).

Plant, specified as a SISO dynamic system model, such as a tf, ss, zpk, or frd model object. If G is a model with tunable or uncertain elements (such as a genss or uss model), then the function uses the current or nominal value of the model.

Loop response to return, specified as a string or character vector. The available loop responses are given in the following table.

Response1-DOF Controller2-DOF ControllerDescription
"open-loop"GC–GCyResponse of the open-loop controller-plant system. Use for frequency-domain design.
Use when your design specifications include robustness criteria such as open-loop gain margin and phase margin.
"closed-loop"

GC1+GC (from r to y)

GCr1−GCy (from r to y)

Closed-loop system response to a step change in setpoint. Use when your design specifications include setpoint tracking.
"controller-effort"

C1+GC (from r to u)

Cr1−GCy (from r to u)

Closed-loop controller output response to a step change in setpoint. Use when your design is limited by practical constraints, such as controller saturation.
"input-disturbance"

G1+GC (from d1 to y)

G1−GCy (from d1 to y)

Closed-loop system response to load disturbance (a step disturbance at the plant input). Use when your design specifications include input disturbance rejection.
"output-disturbance"

11+GC (from d2 to y)

11−GCy (from d2 to y)

Closed-loop system response to a step disturbance at plant output. Use when you want to analyze sensitivity to modeling errors.

Output Arguments

collapse all

Selected loop response, returned as a state-space (ss) or frequency-response data (frd) model. If G is an frd model, then response is also an frd model with the same frequencies as G. Otherwise, response is an ss model.

Version History

Introduced in R2019a

See Also

| | | |