getrom
Description
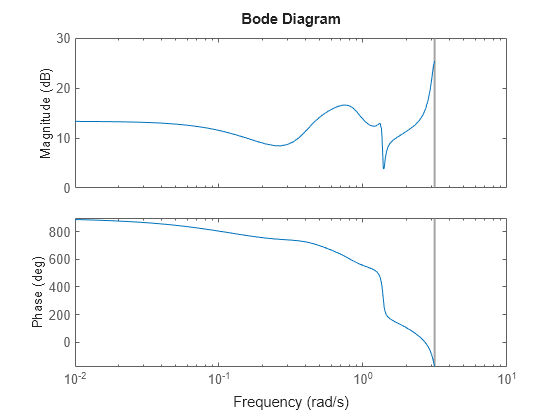
Use getrom to obtain reduced-order models from a
BalancedTruncation or SparseBalancedTruncation model
order reduction task. For the full workflow, see Task-Based Model Order Reduction Workflow.
rsys = getrom(R,Name=Value)rsys based on the options specified by
one or more name-value arguments.
rsys = getrom(R)rsys.
For ordinary balanced truncation,
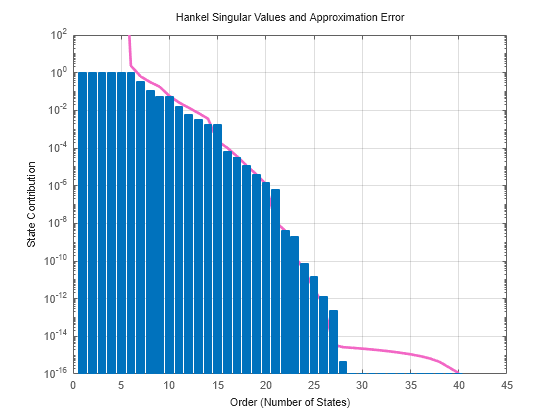
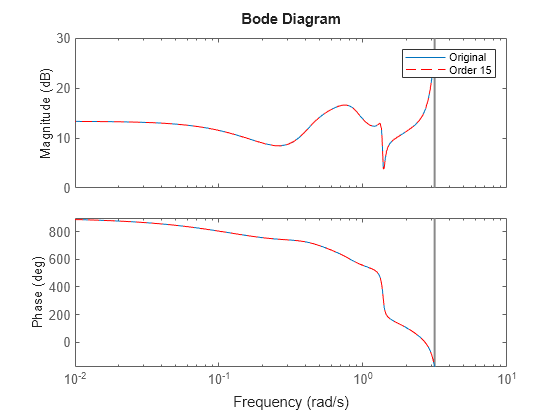
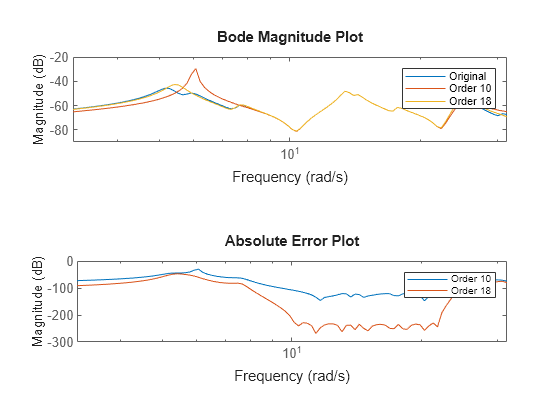
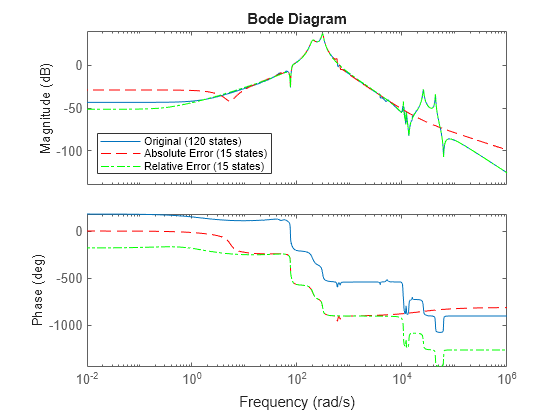
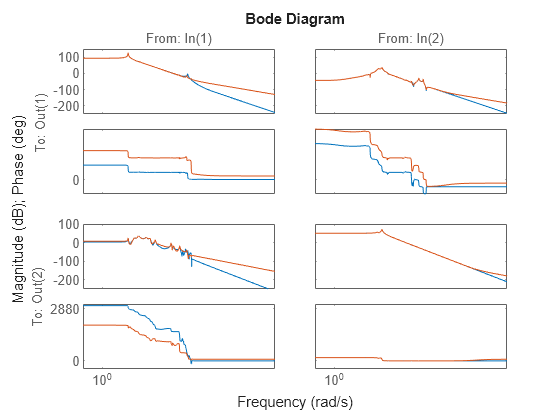
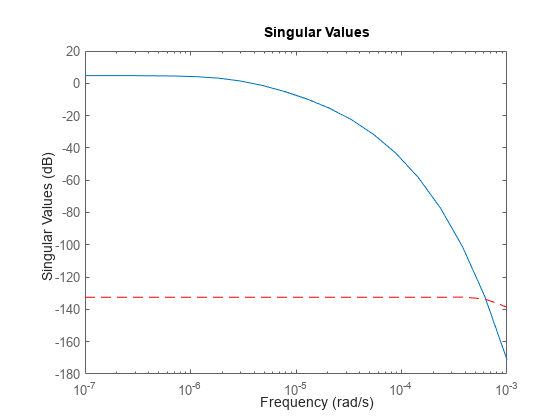
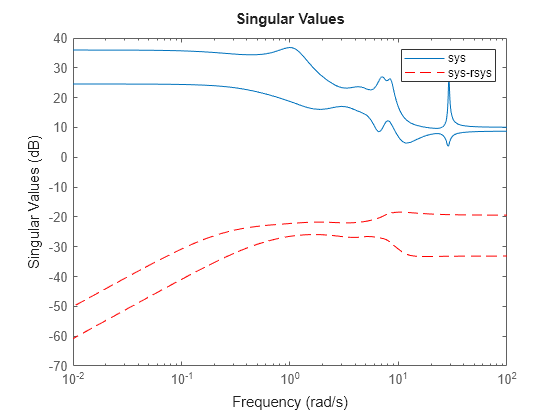
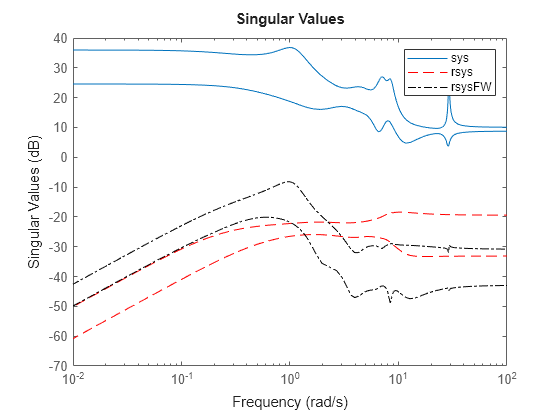
rsysis a simplified model where all states associated with numerically zero Hankel singular values (HSVs) are removed. This amounts to a minimal realization of the original systemsysFor sparse balanced truncation,
rsysis the reduced-order model associated with the computed HSVs. These are the (numerically nonzero) singular values of LrTLo, where Lr and Lo are the low-rank Gramian factors available inR. Since Lr and Lo are tall and skinny, the order ofrsysis typically much smaller than the order ofsys. You can further reduce the order by dropping states with relatively small HSVs.
getrom( returns help specific to
the model order specification object R,"-help")R. The returned help shows the
name-value arguments and syntaxes applicable to R.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] Benner, Peter, Jing-Rebecca Li, and Thilo Penzl. “Numerical Solution of Large-Scale Lyapunov Equations, Riccati Equations, and Linear-Quadratic Optimal Control Problems.” Numerical Linear Algebra with Applications 15, no. 9 (November 2008): 755–77. https://doi.org/10.1002/nla.622.
[2] Benner, Peter, Martin Köhler, and Jens Saak. “Matrix Equations, Sparse Solvers: M-M.E.S.S.-2.0.1—Philosophy, Features, and Application for (Parametric) Model Order Reduction.” In Model Reduction of Complex Dynamical Systems, edited by Peter Benner, Tobias Breiten, Heike Faßbender, Michael Hinze, Tatjana Stykel, and Ralf Zimmermann, 171:369–92. Cham: Springer International Publishing, 2021. https://doi.org/10.1007/978-3-030-72983-7_18.
[3] Varga, A. “Balancing Free Square-Root Algorithm for Computing Singular Perturbation Approximations.” In [1991] Proceedings of the 30th IEEE Conference on Decision and Control, 1062–65. Brighton, UK: IEEE, 1991. https://doi.org/10.1109/CDC.1991.261486.
[4] Green, M. “A Relative Error Bound for Balanced Stochastic Truncation.” IEEE Transactions on Automatic Control 33, no. 10 (October 1988): 961–65. https://doi.org/10.1109/9.7255.