ProperOrthogonalDecomposition
Description
The ProperOrthogonalDecomposition object manages the model order
reduction (MOR) for sparse and ordinary (nonsparse) linear time-invariant (LTI)
models.
Creation
The reducespec
function creates a POD model order reduction object when you use this syntax.
R = reducespec(sys,"pod")Here, sys is a stable LTI model. The workflow uses this object to set up
MOR tasks and store results. For the full workflow, see Task-Based Model Order Reduction Workflow.
Properties
Object Functions
process | Run model order reduction algorithm |
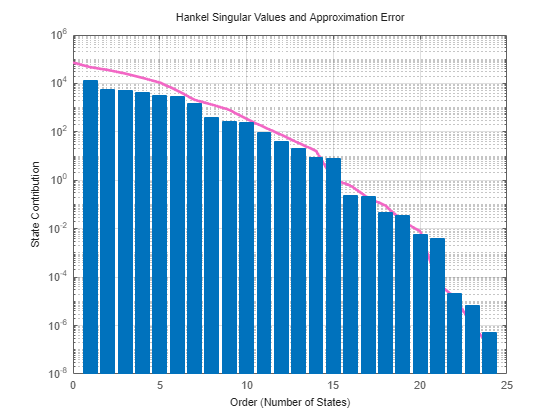
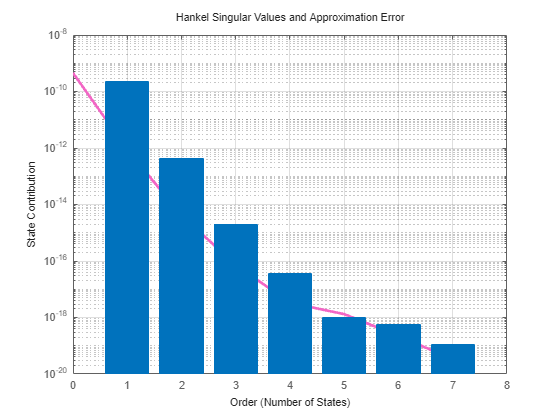
view (pod) | Plot state contributions when using proper orthogonal decomposition (POD) method |
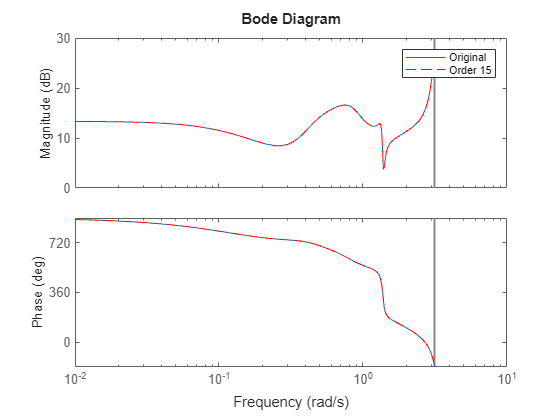
getrom (pod) | Obtain reduced-order models when using proper orthogonal decomposition method |
Examples
Limitations
POD method is applicable only to stable LTI models.
The Galerkin algorithm is recommended specifically for symmetric positive definite problems with A = AT, E = ET ≥ 0 or M = MT ≥ 0, C = CT, K = KT. The algorithm may perform poorly for asymmetric problems because it only takes into account the input-to-state map.
Algorithms
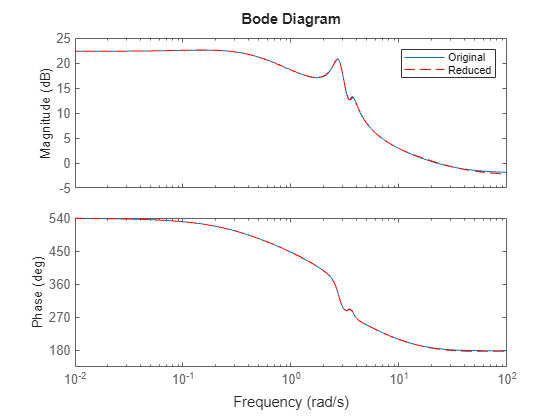
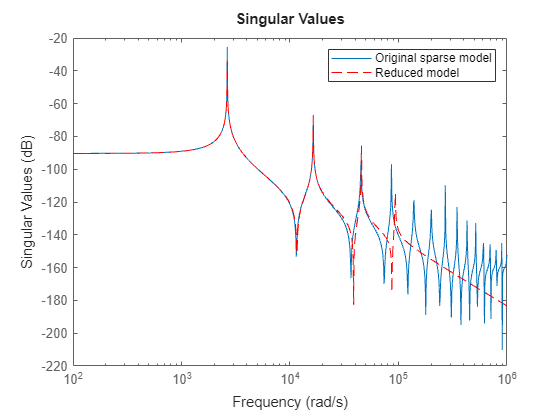
Proper orthogonal decomposition (POD) is a simulation-based technique to extract dominant state directions and perform an approximate Balanced Truncation. This method takes snapshots of the state vector during simulation and uses principal component analysis (PCA) to obtain the principal state directions.
Balanced truncation requires computing the controllability or observability Gramians (see
gram). To approximate these Gramians, the POD
algorithm discretizes the integrals and compresses the state data through incremental SVD
[3].
Consider a SISO model C(sI – A)–1B. The impulse response of this model has state trajectory x(t) = etAB and the controllability Gramian Xr is:
For the adjoint system, the impulse response has state trajectory z(t) = etATCT and the controllability Gramian Xo is:
Suppose you take N + 1 samples of each state snapshots with step size h to form:
The algorithm obtains the Gramian approximations:
Then, the software uses POD to compute low-rank factorizations of the snapshot matrices and obtain the low rank factorizations of the Gramians Xr and Xo:
The software computes this low-rank approximation through an incrementalPOD
object.
When using Balanced algorithm with built-in simulations, the software considers both the input-to-state and state-to-output maps (through the adjoint simulation) to approximate the reachability and observability Gramians. From these approximations, the algorithm proceeds as regular Balanced Truncation by computing the Hankel singular values and suitable left and right projections. If you are providing POD data obtained through custom simulations, to get accurate results, you must simulate both the model and its adjoint to account for both the input-to-state and state-to-output maps.
The Galerkin algorithm considers only input-to-state map, and is applicable only for symmetric problems.
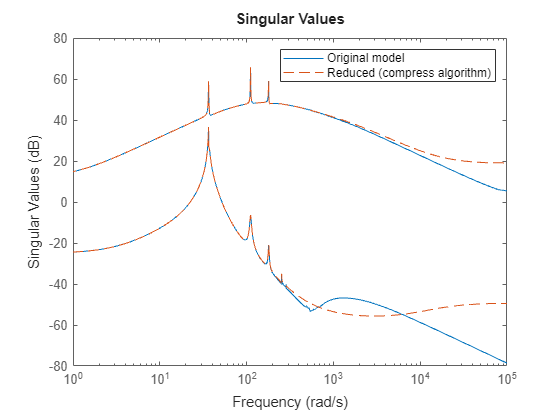
The Compress algorithm is an acceleration of Balanced for tall or wide models (few inputs, many outputs or many inputs, few outputs). The algorithm runs the cheapest simulation (input-to-state if few inputs), uses the resulting POD of X to compress Y=CX, and finds the dominant output directions. Then, performs the adjoint simulation with this reduced Y [4].
For mechss models, the software uses the SOBTpv method [6]. Alternatively, you can
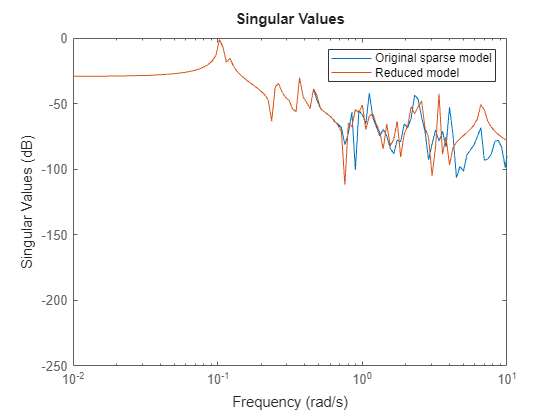
convert mechss models to sparss and use balanced POD on the
result, which may be less efficient but often provides more accurate results.
References
[1] Pinnau, René. “Model Reduction via Proper Orthogonal Decomposition.” In Model Order Reduction: Theory, Research Aspects and Applications, edited by Wilhelmus H. A. Schilders, Henk A. van der Vorst, and Joost Rommes, 95–109. Berlin, Heidelberg: Springer, 2008. https://doi.org/10.1007/978-3-540-78841-6_5.
[2] Liang, Y.C., H.P. Lee, S.P. Lim, W.Z. Lin, K.H. Lee, and C.G. Wu. “PROPER ORTHOGONAL DECOMPOSITION AND ITS APPLICATIONS—PART I: THEORY.” Journal of Sound and Vibration 252, no. 3 (May 2002): 527–44. https://doi.org/10.1006/jsvi.2001.4041.
[3] Willcox, K., and J. Peraire. “Balanced Model Reduction via the Proper Orthogonal Decomposition.” AIAA Journal 40, no. 11 (November 2002): 2323–30. https://doi.org/10.2514/2.1570.
[4] Rowley, C. W. “MODEL REDUCTION FOR FLUIDS, USING BALANCED PROPER ORTHOGONAL DECOMPOSITION.” International Journal of Bifurcation and Chaos 15, no. 03 (March 2005): 997–1013. https://doi.org/10.1142/S0218127405012429.
[5] Moore, B. “Principal Component Analysis in Linear Systems: Controllability, Observability, and Model Reduction.” IEEE Transactions on Automatic Control 26, no. 1 (February 1981): 17–32. https://doi.org/10.1109/TAC.1981.1102568.
[6] Reis, Timo, and Tatjana Stykel. “Balanced Truncation Model Reduction of Second-Order Systems.” Mathematical and Computer Modelling of Dynamical Systems 14, no. 5 (October 2008): 391–406. https://doi.org/10.1080/13873950701844170.
Version History
Introduced in R2024b