拟合幂级数模型
关于幂级数模型
工具箱提供一个单项幂级数模型和一个双项幂级数模型,如下所示
幂级数模型描述各种数据。例如,化学反应中反应物的消耗速率通常与反应物的浓度的某次方成正比。
以交互方式进行幂级数模型拟合
通过在 MATLAB® 命令行中输入
curveFitter打开曲线拟合器。或者,在 App 选项卡上的数学、统计和优化组中,点击曲线拟合器。在曲线拟合器中,选择曲线数据。在曲线拟合器选项卡的数据部分中,点击选择数据。在选择拟合数据对话框中,选择 X 数据和 Y 数据,或仅选择 Y 数据(相对于索引绘图)。
点击拟合类型部分中的箭头以打开库,然后点击回归模型组中的幂。
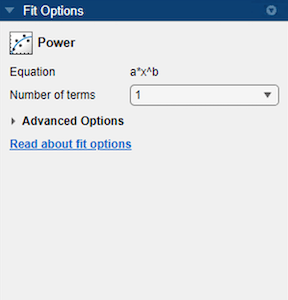
您可以在拟合选项窗格中指定以下选项:
将项的数量指定为
1或2。在结果窗格中查看模型项、系数值和拟合优度统计量。(可选)在高级选项部分,指定系数起始值和约束边界,或更改算法设置。该 App 根据数据集计算优化的幂拟合起点。您可以覆盖起点,并在拟合选项窗格中指定您自己的值。
有关设置的详细信息,请参阅指定拟合选项和优化的起点。
使用拟合函数进行幂级数模型拟合
此示例说明如何使用 fit 函数来对数据进行幂级数模型拟合。
幂级数库模型是 fit 和 fittype 函数的输入参量。指定模型类型 'power1' 或 'power2'。
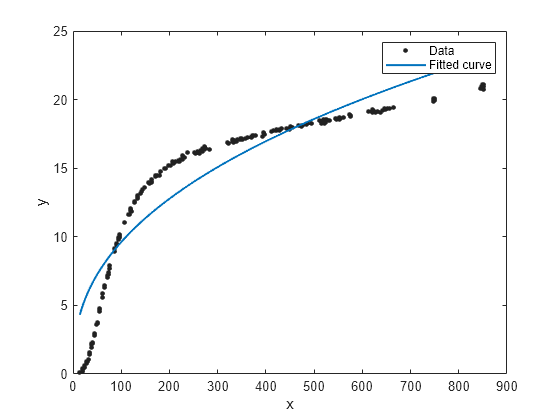
单项幂级数模型拟合
load hahn1; f = fit(temp,thermex,'power1')
f =
General model Power1:
f(x) = a*x^b
Coefficients (with 95% confidence bounds):
a = 1.46 (1.224, 1.695)
b = 0.4094 (0.3825, 0.4363)
plot(f,temp,thermex)
双项幂级数模型拟合
f = fit(temp,thermex,'power2')f =
General model Power2:
f(x) = a*x^b+c
Coefficients (with 95% confidence bounds):
a = -78.61 (-80.74, -76.48)
b = -0.2349 (-0.271, -0.1989)
c = 36.9 (33.09, 40.71)
plot(f,temp,thermex)

另请参阅
App
函数
fit|fittype|fitoptions