使用物理信息神经网络求解 PDE

此示例使用:

此示例说明如何训练物理信息神经网络 (PINN) 来预测偏微分方程 (PDE) 的解。

物理信息神经网络 (PINN) [1] 是一种将物理定律融入其结构体和训练过程的神经网络。例如，您可以训练一个神经网络，输出定义物理系统的 PDE 的解。

此示例训练一个以样本 $(x, t)$ 为输入并输出 $u (x, t)$ 的 PINN，其中 $u$ 是以下伯格斯方程的解：

$\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} - \frac{0.01}{π} \frac{\partial^{2} u}{\partial x^{2}} = 0,$

初始条件为 $u (x, 0) = - s i n (π x)$ ，边界条件为 $u (- 1, t) = 0$ 和 $u (1, t) = 0$ 。

下图说明通过 PINN 的数据流。

Diagram of the data flow of the neural network. The input is x_1, x_2, ... x_N, and t. The output is the PDE solution u(x,t).

训练此模型不需要提前收集数据。您可以使用 PDE 的定义和约束来生成数据。

生成训练数据

训练模型需要一个配置点数据集，这些点用于强制执行边界条件和初始条件并满足伯格斯方程。

选择 25 个等间距的时间点来强制执行每个边界条件 $u (- 1, t) = 0$ 和 $u (1, t) = 0$ 。

numBoundaryConditionPoints = [25 25];

x0BC1 = -1*ones(1,numBoundaryConditionPoints(1));
x0BC2 = ones(1,numBoundaryConditionPoints(2));

t0BC1 = linspace(0,1,numBoundaryConditionPoints(1));
t0BC2 = linspace(0,1,numBoundaryConditionPoints(2));

u0BC1 = zeros(1,numBoundaryConditionPoints(1));
u0BC2 = zeros(1,numBoundaryConditionPoints(2));

选择 50 个等间距的空间点来强制执行初始条件 $u (x, 0) = - s i n (π x)$ 。

numInitialConditionPoints  = 50;

x0IC = linspace(-1,1,numInitialConditionPoints);
t0IC = zeros(1,numInitialConditionPoints);
u0IC = -sin(pi*x0IC);

将初始条件和边界条件的数据组合在一起。

X0 = [x0IC x0BC1 x0BC2];
T0 = [t0IC t0BC1 t0BC2];
U0 = [u0IC u0BC1 u0BC2];

在 $(t, x) \in (0, 1) \times (- 1, 1)$ 范围内均匀采样 10,000 个点，以强制网络输出满足 Burger 方程。

numInternalCollocationPoints = 10000;

points = rand(numInternalCollocationPoints,2);

dataX = 2*points(:,1)-1;
dataT = points(:,2);

定义神经网络架构

定义一个多层感知器神经网络架构。

Diagram of the neual network architecture. The layers are connected in series. The input is passed through 8 fully connected layers that are each proceeded by a tanh layer. The output of the final tanh layer is connected to a fully connected layer, which outputs the network predictions.

对于重复的全连接层，指定输出大小为 20。
对于最终的全连接层，指定输出大小为 1。

指定网络超参数。

numBlocks = 8;
fcOutputSize = 20;

创建神经网络。要轻松构造具有重复层模块的神经网络，您可以使用 repmat 函数重复层模块。

fcBlock = [
    fullyConnectedLayer(fcOutputSize)
    tanhLayer];

layers = [
    featureInputLayer(2)
    repmat(fcBlock,[numBlocks 1])
    fullyConnectedLayer(1)]

layers = 
  18×1 Layer array with layers:

     1   ''   Feature Input     2 features
     2   ''   Fully Connected   20 fully connected layer
     3   ''   Tanh              Hyperbolic tangent
     4   ''   Fully Connected   20 fully connected layer
     5   ''   Tanh              Hyperbolic tangent
     6   ''   Fully Connected   20 fully connected layer
     7   ''   Tanh              Hyperbolic tangent
     8   ''   Fully Connected   20 fully connected layer
     9   ''   Tanh              Hyperbolic tangent
    10   ''   Fully Connected   20 fully connected layer
    11   ''   Tanh              Hyperbolic tangent
    12   ''   Fully Connected   20 fully connected layer
    13   ''   Tanh              Hyperbolic tangent
    14   ''   Fully Connected   20 fully connected layer
    15   ''   Tanh              Hyperbolic tangent
    16   ''   Fully Connected   20 fully connected layer
    17   ''   Tanh              Hyperbolic tangent
    18   ''   Fully Connected   1 fully connected layer

将层数组转换为 dlnetwork 对象。

net = dlnetwork(layers)

net = 
  dlnetwork with properties:

         Layers: [18×1 nnet.cnn.layer.Layer]
    Connections: [17×2 table]
     Learnables: [18×3 table]
          State: [0×3 table]
     InputNames: {'input'}
    OutputNames: {'fc_9'}
    Initialized: 1

  View summary with summary.

当可学习参数为双精度数据类型时，训练 PINN 可以提高准确度。使用 dlupdate 函数将网络可学习参数转换为 double。请注意，并非所有神经网络都支持 double 类型的可学习对象，例如，使用依赖于 single 类型可学习参数的 GPU 优化的网络。

net = dlupdate(@double,net);

定义模型损失函数

创建 modelLoss 函数，该函数以神经网络、网络输入以及初始条件和边界条件为输入，并返回损失关于可学习参数的梯度以及相应损失。

通过强制要求给定输入 $(x, t)$ 时，网络的输出 $u (x, t)$ 满足伯格斯方程、边界条件和初始条件，来训练模型。具体来说，有两个量有助于最小化损失：

$loss = {MSE}_{f} + {MSE}_{u}$ ,

其中 ${MSE}_{f} = \frac{1}{N_{f}} \sum_{i = 1}^{N_{f}} {| f (x_{f}^{i}, t_{f}^{i}) |}^{2}$ 、 ${MSE}_{u} = \frac{1}{N_{u}} \sum_{i = 1}^{N_{u}} {| u (x_{u}^{i}, t_{u}^{i}) - u^{i} |}^{2}$ 、函数 $f$ 位于伯格斯方程的左侧， ${x_{u}^{i}, t_{u}^{i}}_{i = 1}^{N_{u}}$ 对应于计算域边界上的配置点，并考虑了边界条件和初始条件， ${x_{f}^{i}, t_{f}^{i}}_{i = 1}^{N_{f}}$ 是域内部的点。

function [loss,gradients] = modelLoss(net,X,T,X0,T0,U0)

% Make predictions with the initial conditions.
XT = cat(1,X,T);
U = forward(net,XT);

% Calculate derivatives with respect to X and T.
X = stripdims(X);
T = stripdims(T);
U = stripdims(U);
Ux = dljacobian(U,X,1);
Ut = dljacobian(U,T,1);

% Calculate second-order derivatives with respect to X.
Uxx = dldivergence(Ux,X,1);

% Calculate mseF. Enforce Burger's equation.
f = Ut + U.*Ux - (0.01./pi).*Uxx;
mseF = mean(f.^2);

% Calculate mseU. Enforce initial and boundary conditions.
XT0 = cat(1,X0,T0);
U0Pred = forward(net,XT0);
mseU = l2loss(U0Pred,U0);

% Calculated loss to be minimized by combining errors.
loss = mseF + mseU;

% Calculate gradients with respect to the learnable parameters.
gradients = dlgradient(loss,net.Learnables);

end

指定训练选项

指定训练选项：

使用 L-BFGS 求解器进行训练并使用 L-BFGS 求解器状态的默认选项。
进行 1500 次迭代的训练
当梯度或步长的范数小于 $1 0^{- 5}$ 时，提前停止训练。

solverState = lbfgsState;
maxIterations = 1500;
gradientTolerance = 1e-5;
stepTolerance = 1e-5;

训练神经网络

将训练数据转换为 dlarray 对象。指定输入 X 和 T 的格式为 "BC"（批次、通道），初始条件的格式为 "CB"（通道、批次）。

X = dlarray(dataX,"BC");
T = dlarray(dataT,"BC");
X0 = dlarray(X0,"CB");
T0 = dlarray(T0,"CB");
U0 = dlarray(U0,"CB");

使用 dlaccelerate 函数加速损失函数。有关函数加速的详细信息，请参阅Deep Learning Function Acceleration for Custom Training Loops。

accfun = dlaccelerate(@modelLoss);

创建一个包含 L-BFGS 更新步长的损失函数的函数句柄。为了使用自动微分在 modelLoss 函数内计算 dlgradient 函数，请使用 dlfeval 函数。

lossFcn = @(net) dlfeval(accfun,net,X,T,X0,T0,U0);

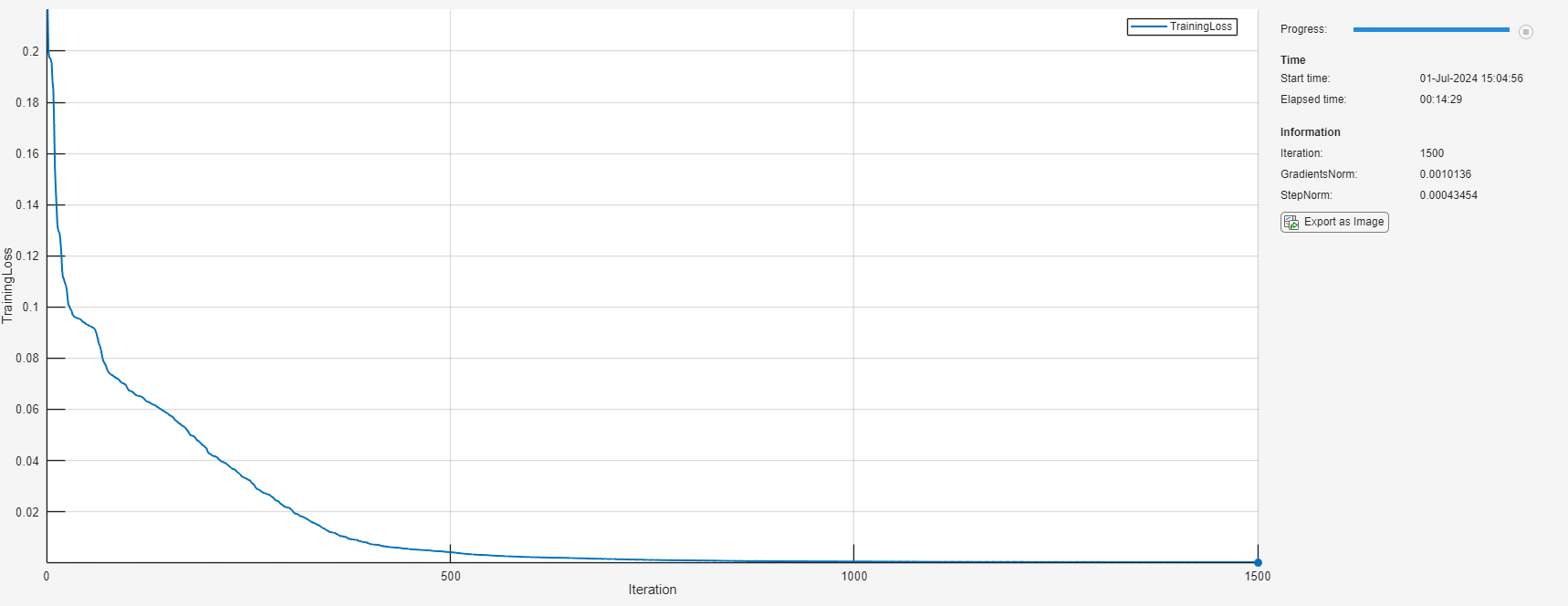
初始化 TrainingProgressMonitor 对象。在每次迭代时，绘制损失并监控梯度和步长的范数。由于计时器在您创建监视器对象时启动，请确保您创建的对象靠近训练循环。

monitor = trainingProgressMonitor( ...
    Metrics="TrainingLoss", ...
    Info=["Iteration" "GradientsNorm" "StepNorm"], ...
    XLabel="Iteration");

在每次迭代时使用完整数据集通过自定义训练循环来训练网络。对于每次迭代：

使用 lbfgsupdate 函数更新网络可学习参数和求解器状态。
更新训练进度监视器。
如果梯度范数小于指定的容差或线搜索失败，则提前停止训练。

iteration = 0;
while iteration < maxIterations && ~monitor.Stop
    iteration = iteration + 1;
    [net, solverState] = lbfgsupdate(net,lossFcn,solverState);

    updateInfo(monitor, ...
        Iteration=iteration, ...
        GradientsNorm=solverState.GradientsNorm, ...
        StepNorm=solverState.StepNorm);

    recordMetrics(monitor,iteration,TrainingLoss=solverState.Loss);

    monitor.Progress = 100*iteration/maxIterations;

    if solverState.GradientsNorm < gradientTolerance || ...
            solverState.StepNorm < stepTolerance || ...
            solverState.LineSearchStatus == "failed"
        break
    end

end

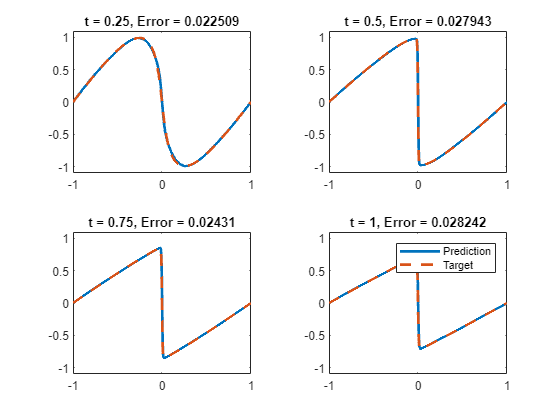
计算模型准确度

对于 $t$ 的值为 0.25、0.5、0.75 和 1 的情况，将深度学习模型的预测值与伯格斯方程的真实解进行比较。

设置测试模型的目标时间。对于每个时间，计算 [-1,1] 范围内 1001 个等间距点的解。

tTest = [0.25 0.5 0.75 1];
numObservationsTest = numel(tTest);

szXTest = 1001;
XTest = linspace(-1,1,szXTest);
XTest = dlarray(XTest,"CB");

测试模型。对于每个测试输入，使用 PINN 预测 PDE 解，并将它们与示例的求解伯格斯方程函数部分中列出的 solveBurgers 函数给出的解进行比较。要访问此函数，请以实时脚本形式打开此示例。通过计算预测值和目标值之间的相对误差来计算准确度。

UPred = zeros(numObservationsTest,szXTest);
UTest = zeros(numObservationsTest,szXTest);

for i = 1:numObservationsTest
    t = tTest(i);

    TTest = repmat(t,[1 szXTest]);
    TTest = dlarray(TTest,"CB");
    XTTest = cat(1,XTest,TTest);

    UPred(i,:) = forward(net,XTTest);
    UTest(i,:) = solveBurgers(extractdata(XTest),t,0.01/pi);
end

err = norm(UPred - UTest) / norm(UTest)

err = 
0.0237

在图中可视化测试预测值。

figure
tiledlayout("flow")

for i = 1:numel(tTest)
    nexttile
    
    plot(XTest,UPred(i,:),"-",LineWidth=2);

    hold on
    plot(XTest, UTest(i,:),"--",LineWidth=2)
    hold off

    ylim([-1.1, 1.1])
    xlabel("x")
    ylabel("u(x," + t + ")")
end

legend(["Prediction" "Target"])

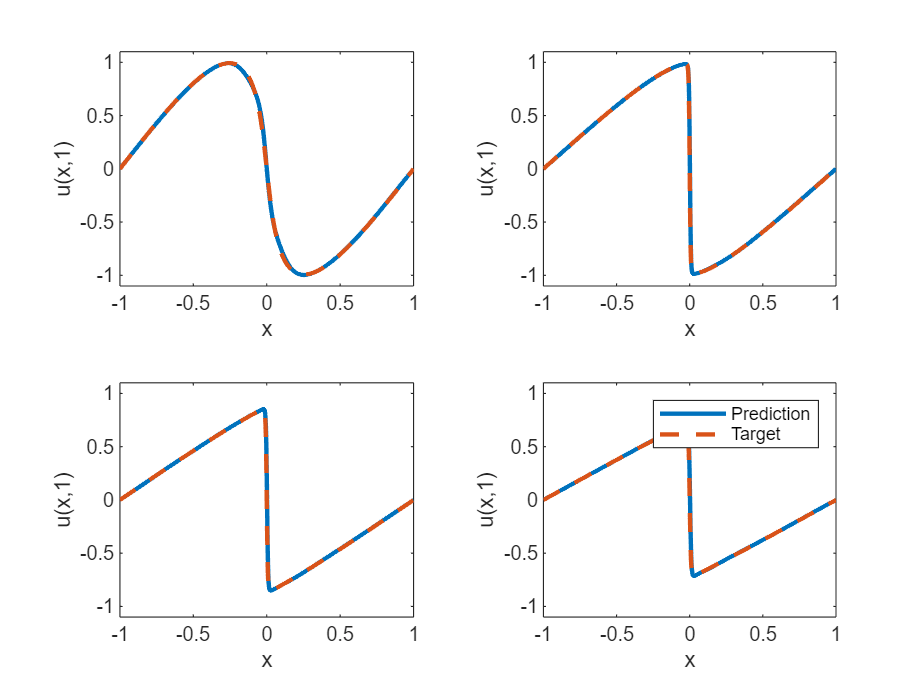
求解伯格斯方程函数

solveBurgers 函数返回伯格斯方程在时间 t 的真实解，如 [2] 中所述。

function U = solveBurgers(X,t,nu)

% Define functions.
f = @(y) exp(-cos(pi*y)/(2*pi*nu));
g = @(y) exp(-(y.^2)/(4*nu*t));

% Initialize solutions.
U = zeros(size(X));

% Loop over x values.
for i = 1:numel(X)
    x = X(i);

    % Calculate the solutions using the integral function. The boundary
    % conditions in x = -1 and x = 1 are known, so leave 0 as they are
    % given by initialization of U.
    if abs(x) ~= 1
        fun = @(eta) sin(pi*(x-eta)) .* f(x-eta) .* g(eta);
        uxt = -integral(fun,-inf,inf);
        fun = @(eta) f(x-eta) .* g(eta);
        U(i) = uxt / integral(fun,-inf,inf);
    end
end

end

参考资料

Maziar Raissi, Paris Perdikaris, and George Em Karniadakis, Physics Informed Deep Learning (Part I):Data-driven Solutions of Nonlinear Partial Differential Equations https://arxiv.org/abs/1711.10561
C. Basdevant, M. Deville, P. Haldenwang, J. Lacroix, J. Ouazzani, R. Peyret, P. Orlandi, A. Patera, Spectral and finite difference solutions of the Burgers equation, Computers & fluids 14 (1986) 23–41.

另请参阅

dlarray | dlfeval | dlgradient