Train Network Using Cyclical Learning Rate for Snapshot Ensembling

Open Live Script

This example shows how to train a network to classify images of objects using a cyclical learning rate schedule and snapshot ensembling for better test accuracy. In the example, you learn how to use a cosine function for the learning rate schedule, take snapshots of the network during training to create a model ensemble, and add L2-norm regularization (weight decay) to the training loss.

This example trains a residual network [1] on the CIFAR-10 data set [2] with a custom cyclical learning rate: for each iteration, the solver uses the learning rate given by a shifted cosine function [3] alpha(t) = (alpha0/2)*cos(pi*mod(t-1,T/M)/(T/M)+1), where t is the iteration number, T is the total number of training iterations, alpha0 is the initial learning rate, and M is the number of cycles/snapshots. This learning rate schedule effectively splits the training process into M cycles. Each cycle begins with a large learning rate that decays monotonically, forcing the network to explore different local minima. At the end of each training cycle, you take a snapshot of the network (that is, you save the model at this iteration) and later average the predictions of all the snapshot models, also known as snapshot ensembling [4], to improve the final test accuracy.

Prepare Data

Download the CIFAR-10 data set [2]. The data set contains 60,000 images. Each image is 32-by-32 in size and has three color channels (RGB). The size of the data set is 175 MB. Depending on your internet connection, the download process can take time.

datadir = tempdir;
downloadCIFARData(datadir);

Load the CIFAR-10 training and test images as 4-D arrays. The training set contains 50,000 images and the test set contains 10,000 images.

[XTrain,TTrain,XTest,TTest] = loadCIFARData(datadir);
classes = categories(TTrain);
numClasses = numel(classes);

You can display a random sample of the training images using the following code.

figure;
idx = randperm(size(XTrain,4),20);
im = imtile(XTrain(:,:,:,idx),ThumbnailSize=[96,96]);
imshow(im)

Create an augmentedImageDatastore object to use for network training. During training, the datastore randomly flips the training images along the vertical axis and randomly translates them up to four pixels horizontally and vertically. Data augmentation helps prevent the network from overfitting and memorizing the exact details of the training images.

imageSize = [32 32 3];
pixelRange = [-4 4];
imageAugmenter = imageDataAugmenter( ...
    RandXReflection=true, ...
    RandXTranslation=pixelRange, ...
    RandYTranslation=pixelRange);
augimdsTrain = augmentedImageDatastore(imageSize,XTrain,TTrain, ...
    DataAugmentation=imageAugmenter);

Define Network Architecture

Create a residual network [1] with six standard convolutional units (two units per stage) and a width of 16. The total network depth is 2*6+2 = 14. In addition, specify the average image using the Mean option in the image input layer.

netWidth = 16;
layers = [
    imageInputLayer(imageSize,Mean=mean(XTrain,4))
    convolution2dLayer(3,netWidth,Padding="same")
    batchNormalizationLayer
    reluLayer(Name="reluInp")

    convolutionalUnit(netWidth,1)
    additionLayer(2,Name="add11")
    reluLayer(Name="relu11")
    convolutionalUnit(netWidth,1)
    additionLayer(2,Name="add12")
    reluLayer(Name="relu12")

    convolutionalUnit(2*netWidth,2)
    additionLayer(2,Name="add21")
    reluLayer(Name="relu21")
    convolutionalUnit(2*netWidth,1)
    additionLayer(2,Name="add22")
    reluLayer(Name="relu22")

    convolutionalUnit(4*netWidth,2)
    additionLayer(2,Name="add31")
    reluLayer(Name="relu31")
    convolutionalUnit(4*netWidth,1)
    additionLayer(2,Name="add32")
    reluLayer(Name="relu32")

    globalAveragePooling2dLayer
    fullyConnectedLayer(numClasses)
    softmaxLayer];

lgraph = layerGraph(layers);
lgraph = connectLayers(lgraph,"reluInp","add11/in2");
lgraph = connectLayers(lgraph,"relu11","add12/in2");

skip1 = [
    convolution2dLayer(1,2*netWidth,Stride=2,Name="skipConv1")
    batchNormalizationLayer(Name="skipBN1")];

lgraph = addLayers(lgraph,skip1);
lgraph = connectLayers(lgraph,"relu12","skipConv1");
lgraph = connectLayers(lgraph,"skipBN1","add21/in2");
lgraph = connectLayers(lgraph,"relu21","add22/in2");

skip2 = [
    convolution2dLayer(1,4*netWidth,Stride=2,Name="skipConv2")
    batchNormalizationLayer(Name="skipBN2")];

lgraph = addLayers(lgraph,skip2);
lgraph = connectLayers(lgraph,"relu22","skipConv2");
lgraph = connectLayers(lgraph,"skipBN2","add31/in2");
lgraph = connectLayers(lgraph,"relu31","add32/in2");

Plot the ResNet architecture.

figure
plot(lgraph)

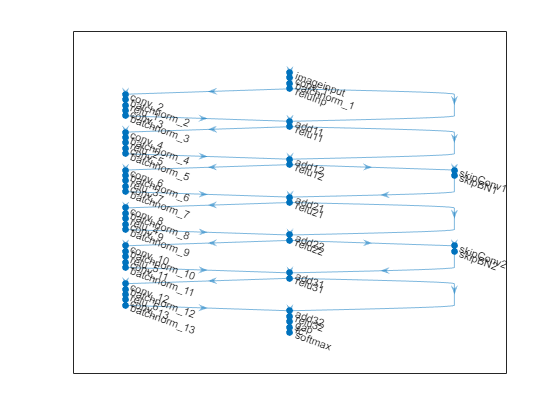
Create a dlnetwork object from the layer graph.

net = dlnetwork(lgraph);

Define Model Loss Function

Create the helper function modelLoss, listed at the end of the example. The function takes in a dlnetwork object net and a mini-batch of input data X with corresponding labels T, and returns the loss, the gradients of the loss with respect to the learnable parameters in net, and the state of the nonlearnable parameters of the network at a given iteration.

Specify Training Options

Specify the training options.

Train for 200 epochs with a mini-batch size of 64.
Train using SGDM with a momentum of 0.9.
Regularize the weights using a weight decay value of $1 0^{- 4}$ .

numEpochs = 200;
miniBatchSize = 64;
momentum = 0.9;
weightDecay = 1e-4;

Determine the indices of the weights to apply weight decay to.

idxWeights = ismember(net.Learnables.Parameter,["Weights" "Scale"]);

Initialize the parameters for SGDM optimization.

velocity = [];

Specify the training options specific to the cyclical learning rate. alpha0 is the initial learning rate and numSnapshots is the number of cycles or snapshots taken during training.

alpha0 = 0.1;
numSnapshots = 5;
epochsPerSnapshot = numEpochs./numSnapshots;
numObservations = numel(TTrain);
iterationsPerSnapshot = ceil(numObservations./miniBatchSize)*numEpochs./numSnapshots;
modelPrefix = "SnapshotEpoch";

Initialize the training figure.

[lossLine,learnRateLine] = plotLossAndLearnRate;

Train Model

Use minibatchqueue to process and manage mini-batches of images during training. For each mini-batch:

Use the custom mini-batch preprocessing function preprocessMiniBatch (defined at the end of this example) to one-hot encode the class labels.
Format the image data with the dimension labels "SSCB" (spatial, spatial, channel, batch). By default, the minibatchqueue object converts the data to dlarray objects with underlying type single. Do not add a format to the class labels.
Train on a GPU if one is available. By default, the minibatchqueue object converts each output to a gpuArray if a GPU is available. Using a GPU requires Parallel Computing Toolbox™ and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox).

augimdsTrain.MiniBatchSize = miniBatchSize;

mbqTrain = minibatchqueue(augimdsTrain,...
    MiniBatchSize=miniBatchSize,...
    MiniBatchFcn=@preprocessMiniBatch,...
    MiniBatchFormat=["SSCB",""]);

Accelerate the modelLoss function using dlaccelerate.

accfun = dlaccelerate(@modelLoss);

Train the model using a custom training loop. For each epoch, shuffle the datastore, loop over mini-batches of data, and save the model (snapshot) if the current epoch is a multiple of epochsPerSnapshot. At the end of each epoch, display the training progress. For each mini-batch:

Evaluate the model loss and gradients using dlfeval and the accelerated modelLoss function.
Update the state of the nonlearnable parameters of the network.
Determine the learning rate for the cyclical learning rate schedule.
Update the network parameters using the sgdmupdate function.
Plot the loss and learning rate at each iteration.

For this example, the training took approximately 11 hours on a NVIDIA™ TITAN RTX.

iteration = 0;
start = tic;

% Loop over epochs.
for epoch = 1:numEpochs

    % Shuffle data.
    shuffle(mbqTrain);

    % Save snapshot model.
    if ~mod(epoch,epochsPerSnapshot)
        save(modelPrefix + epoch + ".mat","net");
    end

    % Loop over mini-batches.
    while hasdata(mbqTrain)
        iteration = iteration + 1;

        % Read mini-batch of data.
        [X,T] = next(mbqTrain);

        % Evaluate the model loss and gradients using dlfeval and the
        % accelerated modelLoss function.
        [loss, gradients, state] = dlfeval(accfun,net,X,T,weightDecay,idxWeights);

        % Update the state of nonlearnable parameters.
        net.State = state;

        % Determine learning rate for cyclical learning rate schedule.
        learnRate = 0.5*alpha0*(cos((pi*mod(iteration-1,iterationsPerSnapshot)./iterationsPerSnapshot))+1);

        % Update the network parameters using the SGDM optimizer.
        [net, velocity] = sgdmupdate(net, gradients, velocity, learnRate, momentum);

        % Display the training progress.
        D = duration(0,0,toc(start),Format="hh:mm:ss");
        addpoints(lossLine,iteration,double(loss))
        addpoints(learnRateLine, iteration, learnRate);
        sgtitle("Epoch: " + epoch + ", Elapsed: " + string(D))
        drawnow
    end
end

Create Snapshot Ensemble and Test Model

Combine the M snapshots of the network taken during training to form a final ensemble and test the classification accuracy of the model. The ensemble predictions correspond to the average of the output of the fully connected layer from all M individual models.

Test the model on the test data provided with the CIFAR-10 data set. Manage the test data set using a minibatchqueue object with the same setting as the training data.

augimdsTest = augmentedImageDatastore(imageSize,XTest,TTest);
augimdsTest.MiniBatchSize = miniBatchSize;

mbqTest = minibatchqueue(augimdsTest,...
    MiniBatchSize=miniBatchSize,...
    MiniBatchFcn=@preprocessMiniBatch,...
    MiniBatchFormat=["SSCB",""]);

Evaluate the accuracy of each snapshot network. Use the modelPredictions function defined at the end of this example to iterate over all the data in the test data set. The function returns the output of the fully connected layer from the model, the predicted classes, and the comparison with the true class.

modelName = cell(numSnapshots+1,1);
fcOutput = zeros(numClasses,numel(TTest),numSnapshots+1);
classPredictions = cell(1,numSnapshots+1);
modelAccuracy = zeros(numSnapshots+1,1);

for m = 1:numSnapshots
    modelName{m} = modelPrefix + m*epochsPerSnapshot;
    load(modelName{m} + ".mat");

    reset(mbqTest);
    [fcOutputTest,classPredTest,classCorrTest] = modelPredictions(net,mbqTest,classes);

    fcOutput(:,:,m) = fcOutputTest;
    classPredictions{m} = classPredTest;
    modelAccuracy(m) = 100*mean(classCorrTest);

    disp(modelName{m} + " accuracy: " + modelAccuracy(m) + "%")
end

SnapshotEpoch40 accuracy: 87.93%
SnapshotEpoch80 accuracy: 89.92%
SnapshotEpoch120 accuracy: 90.55%
SnapshotEpoch160 accuracy: 90.67%
SnapshotEpoch200 accuracy: 91.33%

To determine the output of the ensemble networks, compute the average of the fully connected output of each snapshot network. Find the predicted classes from the ensemble network using the onehotdecode function. Compare with the true classes to evaluate the accuracy of the ensemble.

fcOutput(:,:,end) = mean(fcOutput(:,:,1:end-1),3);
classPredictions{end} = onehotdecode(softmax(fcOutput(:,:,end)),classes,1,"categorical");

classCorrEnsemble = classPredictions{end} == TTest';
modelAccuracy(end) = 100*mean(classCorrEnsemble);

modelName{end} = "Ensemble model";
disp("Ensemble accuracy: " + modelAccuracy(end) + "%")

Ensemble accuracy: 91.74%

Plot Accuracy

Plot the accuracy on the test data set for all snapshot models and the ensemble model.

figure;bar(modelAccuracy);
ylabel("Accuracy (%)");
xticklabels(modelName)
xtickangle(45)
title("Model accuracy")

Helper Functions

Model Loss Function

The modelLoss function takes in a dlnetwork object net, a mini-batch of input data X, the labels T, the parameter for weight decay, and the indices of the weights to decay. The function returns the loss, the gradients, and the state of the nonlearnable parameters. To compute the gradients automatically, use the dlgradient function.

function [loss,gradients,state] = modelLoss(net,X,T,weightDecay,idxWeights)

[Y,state] = forward(net,X);

loss = crossentropy(Y, T);

% L2-regularization (weight decay)
allParams = net.Learnables(idxWeights,:).Value;
L = dlupdate(@(x) sum(x.^2,"all"),allParams);
L = sum(cat(1,L{:}));
loss = loss + weightDecay*0.5*L;

gradients = dlgradient(loss,net.Learnables);

end

Model Predictions Function

The modelPredictions function takes as input a dlnetwork object net, a minibatchqueue of input data mbq, and computes the model predictions by iterating over all data in the minibatchqueue. The function uses the onehotdecode function to find the predicted class with the highest score and then compares the prediction with the true class. The function returns the network output, the class predictions, and a vector of ones and zeros that represents correct and incorrect predictions.

function [rawPredictions,classPredictions,classCorr] = modelPredictions(net,mbq,classes)

rawPredictions = [];
classPredictions = [];
classCorr = [];

while hasdata(mbq)
    [X,T] = next(mbq);

    % Make predictions
    YPred = predict(net,X);
    rawPredictions = [rawPredictions extractdata(gather(YPred))];

    % Convert network output to probabilities and determine predicted
    % classes
    YPred = softmax(YPred);
    YPredBatch = onehotdecode(YPred,classes,1);
    classPredictions = [classPredictions YPredBatch];

    % Compare predicted and true classes
    T = onehotdecode(T,classes,1);
    classCorr = [classCorr YPredBatch == T];
end

end

Plot Loss and Learning Rate Function

The plotLossAndLearnRate function initiliaizes the plots for displaying the loss and learning rate at each iteration during training.

function [lossLine, learnRateLine] = plotLossAndLearnRate

figure
subplot(2,1,1);

lossLine = animatedline(Color=[0.85 0.325 0.098]);
title("Loss");
xlabel("Iteration")
ylabel("Loss")
grid on

subplot(2,1,2);
learnRateLine = animatedline(Color=[0 0.447 0.741]);
title("Learning rate");
xlabel("Iteration")
ylabel("Learning rate")
grid on

end

Convolutional Unit Function

The convolutionalUnit(numF,stride) function creates an array of layers with two convolutional layers and corresponding batch normalization and ReLU layers. numF is the number of convolutional filters and stride is the stride of the first convolutional layer.

function layers = convolutionalUnit(numF,stride)

layers = [
    convolution2dLayer(3,numF,Padding="same",Stride=stride)
    batchNormalizationLayer
    reluLayer
    convolution2dLayer(3,numF,Padding="same")
    batchNormalizationLayer];

end

Data Preprocessing Function

The preprocessMiniBatch function preprocesses the data using the following steps:

Extract the image data from the incoming cell array and concatenate into a numeric array. Concatenating the image data over the fourth dimension adds a third dimension to each image, to be used as a singleton channel dimension.
Extract the label data from the incoming cell arrays and concatenate into a categorical array along the second dimension.
One-hot encode the categorical labels into numeric arrays. Encoding into the first dimension produces an encoded array that matches the shape of the network output.

function [X,T] = preprocessMiniBatch(XCell,TCell)

% Extract image data from cell and concatenate
X = cat(4,XCell{:});

% Extract label data from cell and concatenate
T = cat(2,TCell{:});

% One-hot encode labels
T = onehotencode(T,1);

end

References

[1] He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. "Deep residual learning for image recognition." In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 770-778. 2016.

[2] Krizhevsky, Alex. "Learning multiple layers of features from tiny images." (2009). https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf

[3] Loshchilov, Ilya, and Frank Hutter. "Sgdr: Stochastic gradient descent with warm restarts." (2016). arXiv preprint arXiv:1608.03983.

[4] Huang, Gao, Yixuan Li, Geoff Pleiss, Zhuang Liu, John E. Hopcroft, and Kilian Q. Weinberger. "Snapshot ensembles: Train 1, get m for free." (2017). arXiv preprint arXiv:1704.00109.