Calibrating Hull-White Model Using Market Data
The pricing of interest-rate derivative securities relies on models that describe the underlying process. These interest rate models depend on one or more parameters that you must determine by matching the model predictions to the existing data available in the market. In the Hull-White model, there are two parameters related to the short rate process: mean reversion and volatility. Calibration is used to determine these parameters, such that the model can reproduce, as close as possible, the prices of caps or floors observed in the market. The calibration routines find the parameters that minimize the difference between the model price predictions and the market prices for caps and floors.
For a Hull-White model, the minimization is two dimensional, with respect to mean reversion (α) and volatility (σ). That is, calibrating the Hull-White model minimizes the difference between the model’s predicted prices and the observed market prices of the corresponding caplets or floorlets.
Hull-White Model Calibration Example
Use market data to identify the implied volatility (σ) and mean reversion (α)
coefficients needed to build a Hull-White tree to price an instrument. The ideal
case is to use the volatilities of the caps or floors used to calculate
Alpha (α) and Sigma (σ). This will most
likely not be the case, so market data must be interpolated to obtain the required
values.
Consider a cap with these parameters:
Settle = 'Jan-21-2008'; Maturity = 'Mar-21-2011'; Strike = 0.0690; Reset = 4; Principal = 1000; Basis = 0;
The caplets for this example would fall in:
capletDates = cfdates(Settle, Maturity, Reset, Basis); datestr(capletDates')
ans = 21-Mar-2008 21-Jun-2008 21-Sep-2008 21-Dec-2008 21-Mar-2009 21-Jun-2009 21-Sep-2009 21-Dec-2009 21-Mar-2010 21-Jun-2010 21-Sep-2010 21-Dec-2010 21-Mar-2011
In the best case, look up the market volatilities for caplets with a
Strike = 0.0690, and maturities in each
reset date listed, but the likelihood of finding these exact instruments is low. As
a consequence, use data that is available in the market and interpolate to find
appropriate values for the caplets.
Based on the market data, you have the cap information for different dates and
strikes. Assume that instead of having the data for Strike =
0.0690, you have the data for Strike1 =
0.0590 and Strike2 =
0.0790.
| Maturity | Strike1 = 0.0590 | Strike2 = 0.0790 |
|---|---|---|
| 21-Mar-2008 | 0.1533 | 0. 1526 |
| 21-Jun-2008 | 0.1731 | 0. 1730 |
| 21-Sep-2008 | 0. 1727 | 0. 1726 |
| 21-Dec-2008 | 0. 1752 | 0. 1747 |
| 21-Mar-2009 | 0. 1809 | 0. 1808 |
| 21-Jun-2009 | 0. 1809 | 0. 1792 |
| 21-Sep-2009 | 0. 1805 | 0. 1797 |
| 21-Dec-2009 | 0. 1802 | 0. 1794 |
| 21-Mar-2010 | 0. 1802 | 0. 1733 |
| 21-Jun-2010 | 0. 1757 | 0. 1751 |
| 21-Sep-2010 | 0. 1755 | 0. 1750 |
| 21-Dec-2010 | 0. 1755 | 0. 1745 |
| 21-Mar-2011 | 0. 1726 | 0. 1719 |
The nature of this data lends itself to matrix nomenclature, which is perfect for
MATLAB®. hwcalbycap requires that the
dates, the strikes, and the actual volatility be separated into three variables:
MarketStrike, MarketMat, and
MarketVol.
MarketStrike = [0.0590; 0.0790]; MarketMat = [datetime(2008,3,21) ; datetime(2008,6,21) ; datetime(2008,9,21) ; datetime(2008,12,21) ; datetime(2009,3,21) ; ... datetime(2009,6,21) ; datetime(2009,9,21) ; datetime(2009,12,21); datetime(2010,3,21) ; ... datetime(2010,6,21); datetime(2010,9,21) ; datetime(2010,12,21) ; datetime(2011,3,21)]; MarketVol = [0.1533 0.1731 0.1727 0.1752 0.1809 0.1800 0.1805 0.1802 0.1735 0.1757 ... 0.1755 0.1755 0.1726; % First row in table corresponding to Strike1 0.1526 0.1730 0.1726 0.1747 0.1808 0.1792 0.1797 0.1794 0.1733 0.1751 ... 0.1750 0.1745 0.1719]; % Second row in table corresponding to Strike2
Complete the input arguments using this data for
RateSpec:
Rates = [0.0627; 0.0657; 0.0691; 0.0717; 0.0739; 0.0755; 0.0765; 0.0772; 0.0779; 0.0783; 0.0786; 0.0789; 0.0792; 0.0793]; ValuationDate = datetime(2008,1,21); EndDates = [datetime(2008,3,21) ; datetime(2008,6,21) ; datetime(2008,9,21) ; datetime(2008,12,21) ; ... datetime(2009,3,21) ; datetime(2009,6,21) ; datetime(2009,9,21) ; datetime(2009,12,21); datetime(2010,3,21) ; ... datetime(2010,6,21); datetime(2010,9,21) ; datetime(2010,12,21) ; datetime(2011,3,21) ; datetime(2011,6,21)]; Compounding = 4; Basis = 0; RateSpec = intenvset('ValuationDate', ValuationDate, ... 'StartDates', ValuationDate, 'EndDates', EndDates, ... 'Rates', Rates, 'Compounding', Compounding, 'Basis', Basis)
RateSpec =
FinObj: 'RateSpec'
Compounding: 4
Disc: [14x1 double]
Rates: [14x1 double]
EndTimes: [14x1 double]
StartTimes: [14x1 double]
EndDates: [14x1 double]
StartDates: 733428
ValuationDate: 733428
Basis: 0
EndMonthRule: 1Call the calibration routine to find values for volatility parameters Alpha and Sigma
Use hwcalbycap to calculate the
values of Alpha and Sigma based on market
data. Internally, hwcalbycap calls the function
lsqnonlin. You can customize
lsqnonlin by passing an
optimization options structure created by optimoptions and then this can be
passed to hwcalbycap using the
name-value pair argument for OptimOptions. For example,
optimoptions defines the target
objective function tolerance as 100*eps and then calls
hwcalbycap:
o=optimoptions('lsqnonlin','TolFun',100*eps); [Alpha, Sigma] = hwcalbycap(RateSpec, MarketStrike, MarketMat, MarketVol, ... Strike, Settle, Maturity, 'Reset', Reset, 'Principal', Principal, 'Basis', ... Basis, 'OptimOptions', o)
Local minimum possible.
lsqnonlin stopped because the size of the current step is less than
the default value of the step size tolerance.
Warning: LSQNONLIN did not converge to an optimal solution. It exited with exitflag = 2.
> In hwcalbycapfloor at 93
In hwcalbycap at 75
Alpha =
1.0000e-06
Sigma =
0.0127 The previous warning indicates that the conversion was not optimal. The
search algorithm used by the Optimization Toolbox™ function lsqnonlin did not find a solution
that conforms to all the constraints. To discern whether the solution is
acceptable, look at the results of the optimization by specifying a third output
(OptimOut) for hwcalbycap:
[Alpha, Sigma, OptimOut] = hwcalbycap(RateSpec, MarketStrike, MarketMat, ... MarketVol, Strike, Settle, Maturity, 'Reset', Reset, 'Principal', Principal, ... 'Basis', Basis, 'OptimOptions', o);
The OptimOut.residual field of the
OptimOut structure is the optimization residual. This
value contains the difference between the Black caplets and those calculated
during the optimization. You can use the OptimOut.residual
value to calculate the percentual difference (error) compared to Black caplet
prices and then decide whether the residual is acceptable. There is almost
always some residual, so decide if it is acceptable to parameterize the market
with a single value of Alpha and
Sigma.
Price caplets using market data and Black's formula to obtain reference caplet values
To determine the effectiveness of the optimization, calculate reference caplet values using Black’s formula and the market data. Note, you must first interpolate the market data to obtain the caplets for calculation:
[Mats, Strikes] = meshgrid(MarketMat, MarketStrike);
MarketMat_T = yearfrac(Settle,Mats);
Mats_T = yearfrac(Settle,Maturity);
FlatVol = interp2(MarketMat_T, Strikes, MarketVol, Mats_T, Strike, 'spline');
Compute the price of the cap using the Black model:
[CapPrice, Caplets] = capbyblk(RateSpec, Strike, Settle, Maturity, FlatVol, ... 'Reset', Reset, 'Basis', Basis, 'Principal', Principal); Caplets = Caplets(2:end)';
Caplets =
0.3210
1.6355
2.4863
3.1903
3.4110
3.2685
3.2385
3.4803
3.2419
3.1949
3.2991
3.3750Compare optimized values and Black values and display graphically
After calculating the reference values for the caplets, compare the values,
analytically and graphically, to determine whether the calculated single values
of Alpha and Sigma provide an adequate
approximation:
OptimCaplets = Caplets+OptimOut.residual; disp(' '); disp(' Black76 Calibrated Caplets'); disp([Caplets OptimCaplets]) plot(MarketMat(2:end), Caplets, 'or', MarketMat(2:end), OptimCaplets, '*b'); xtickformat; xlabel('Caplet Maturity'); ylabel('Caplet Price'); title('Black and Calibrated Caplets'); h = legend('Black Caplets', 'Calibrated Caplets'); set(h, 'color', [0.9 0.9 0.9]); set(h, 'Location', 'SouthEast'); set(gcf, 'NumberTitle', 'off') grid on
Black76 Calibrated Caplets
0.3210 0.3636
1.6355 1.6603
2.4863 2.4974
3.1903 3.1874
3.4110 3.4040
3.2685 3.2639
3.2385 3.2364
3.4803 3.4683
3.2419 3.2408
3.1949 3.1957
3.2991 3.2960
3.3750 3.3663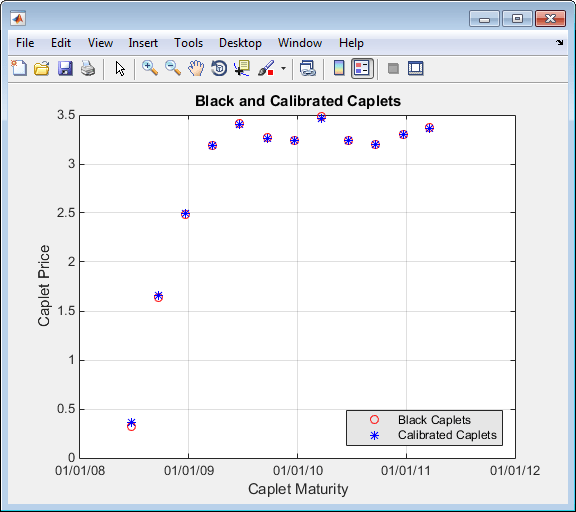
Compare cap prices using the Black, HW analytical, and HW tree models
Using the calculated caplet values, compare the prices of the corresponding
cap using the Black model, Hull-White analytical, and Hull-White tree models. To
calculate a Hull-White tree based on Alpha and
Sigma, use these calibration routines:
Black model:
CapPriceBLK = CapPrice;
HW analytical model:
CapPriceHWAnalytical = sum(OptimCaplets);
HW tree model to price the cap derived from the calibration process:
Create
VolSpecfrom the calibration parametersAlphaandSigma:VolDates = EndDates; VolCurve = Sigma*ones(14,1); AlphaDates = EndDates; AlphaCurve = Alpha*ones(14,1); HWVolSpec = hwvolspec(ValuationDate, VolDates, VolCurve,AlphaDates, AlphaCurve);
Create the
TimeSpec:HWTimeSpec = hwtimespec(ValuationDate, EndDates, Compounding);
Build the HW tree using the
HW2000method:HWTree = hwtree(HWVolSpec, RateSpec, HWTimeSpec, 'Method', 'HW2000');
Price the cap:
Price = capbyhw(HWTree, Strike, Settle, Maturity, Reset, Basis, Principal); disp(' '); disp([' CapPrice Black76 ..................: ', num2str(CapPriceBLK,'%15.5f')]); disp([' CapPrice HW analytical..........: ', num2str(CapPriceHWAnalytical,'%15.5f')]); disp([' CapPrice HW from capbyhw ..: ', num2str(Price,'%15.5f')]); disp(' ');
CapPrice Black76 ..........: 34.14220 CapPrice HW analytical.....: 34.18008 CapPrice HW from capbyhw ..: 34.14192
Price a portfolio of instruments using the calibrated HW tree
After building a Hull-White tree, based on parameters calibrated from market
data, use HWTree to price a portfolio of these instruments:
Two bonds
CouponRate = [0.07; 0.09]; Settle = 'Jan-21-2008'; Maturity = {'Mar-21-2010';'Mar-21-2011'}; Period = 1; Face = 1000; Basis = 0;
Bond with an embedded American call option
CouponRateOEB = 0.08; SettleOEB = 'Jan-21-2008'; MaturityOEB = 'Mar-21-2011'; OptSpec = 'call'; StrikeOEB = 950; ExerciseDatesOEB = 'Mar-21-2011'; AmericanOpt = 1; Period = 1; Face = 1000; Basis = 0;
To price this portfolio of instruments using the calibrated
HWTree:
Use
instaddto create the portfolioInstSet:InstSet = instadd('Bond', CouponRate, Settle, Maturity, Period, Basis, [], [], [], [], [], Face); InstSet = instadd(InstSet,'OptEmBond', CouponRateOEB, SettleOEB, MaturityOEB, OptSpec, ... StrikeOEB, ExerciseDatesOEB, 'AmericanOpt', AmericanOpt, 'Period', Period, ... 'Face',Face, 'Basis', Basis);
Add the cap instrument used in the calibration:
SettleCap = ' Jan-21-2008'; MaturityCap = 'Mar-21-2011'; StrikeCap = 0.0690; Reset = 4; Principal = 1000; InstSet = instadd(InstSet,'Cap', StrikeCap, SettleCap, MaturityCap, Reset, Basis, Principal);
Assign names to the portfolio instruments:
Names = {'7% Bond'; '8% Bond'; 'BondEmbCall'; '6.9% Cap'}; InstSet = instsetfield(InstSet, 'Index',1:4, 'FieldName', {'Name'}, 'Data', Names );Examine the set of instruments contained in
InstSet:instdisp(InstSet)
IdxType CoupRate Settle Mature Period Basis EOMRule IssueDate 1stCoupDate LastCoupDate StartDate Face Name 1 Bond 0.07 21-Jan-2008 21-Mar-2010 1 0 NaN NaN NaN NaN NaN 1000 7% Bond 2 Bond 0.09 21-Jan-2008 21-Mar-2011 1 0 NaN NaN NaN NaN NaN 1000 8% Bond IdxType CoupRate Settle Mature OptSpec Stke ExDate Per Basis EOMRule IssDate 1stCoupDate LstCoupDate StrtDate Face AmerOpt Name 3 OptEmBond 0.08 21-Jan-2008 21-Mar-2011 call 950 21-Jan-2008 21-Mar-2011 1 0 1 NaN NaN NaN NaN 1000 1 BondEmbCall Index Type Strike Settle Maturity CapReset Basis Principal Name 4 Cap 0.069 21-Jan-2008 21-Mar-2011 4 0 1000 6.9% Cap
Use
hwpriceto price the portfolio using the calibratedHWTree:format bank PricePortfolio = hwprice(HWTree, InstSet)PricePortfolio = 980.45 1023.05 945.73 34.14
See Also
instbond | instcap | instoptbnd | instoptembnd | intenvset | hwtimespec | hwtree | hwvolspec | bondbyhw | capbyhw | hwcalbycap | hwcalbyfloor | hwprice | hwsens
Topics
- Overview of Interest-Rate Tree Models
- Pricing Using Interest-Rate Tree Models
- Graphical Representation of Trees
- Understanding Interest-Rate Tree Models
- Understanding Interest-Rate Term Structure
- Pricing Using Interest-Rate Term Structure
- Supported Interest-Rate Instrument Functions
- Supported Equity Derivative Functions
- Supported Energy Derivative Functions
- Mapping Financial Instruments Toolbox Functions for Interest-Rate Instrument Objects