GlobalSearch 和 MultiStart 的工作原理
局部求解器的多次运行
GlobalSearch 和 MultiStart 有类似的方法来寻找全局或多个极小值。两种算法都从多个起点启动局部求解器(例如 fmincon)。该算法使用多个起点来对多个吸引盆进行采样。有关详细信息,请参阅吸引盆。
求解器对象之间的差异
GlobalSearch 和 MultiStart 算法概述 包含 GlobalSearch 和 MultiStart 算法的草图。
GlobalSearch 和 MultiStart 算法概述
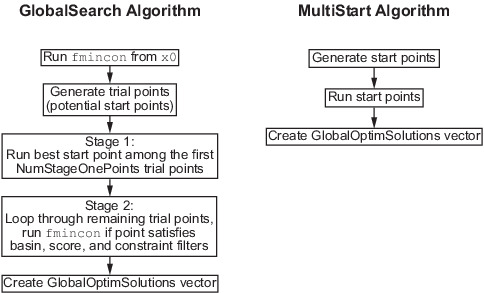
GlobalSearch 和 MultiStart 的主要区别在于:
GlobalSearch使用散射搜索机制来生成起点。MultiStart使用边界内均匀分布的起点,或者用户提供的起点。GlobalSearch分析起点并拒绝那些不太可能改善迄今为止找到的最佳局部最小值的点。MultiStart运行所有起点(或者,可选地,所有相对于边界或不等式约束可行的起点)。MultiStart提供局部求解器的选择:fmincon、fminunc、lsqcurvefit或lsqnonlin。GlobalSearch算法使用fmincon。MultiStart可以并行运行,将起点分发到多个处理器以进行局部解。要并行运行MultiStart,请参阅 如何在 Global Optimization Toolbox 中使用并行处理。
决定使用哪个求解器
这些求解器对象之间的差异可以归结为以下关于使用哪一个的决定:
使用
GlobalSearch在单个处理器上最有效地找到单个全局最小值。使用
MultiStart:找到多个局部极小值。
并行运行。
使用
fmincon以外的求解器。彻底搜索以找到全局最小值。
探索您自己的起点。
GlobalSearch 算法
有关该算法的描述,请参阅 Ugray 等人的 [1]。
当您 run 一个 GlobalSearch 对象时,算法执行以下步骤:
从 x0 运行 fmincon
GlobalSearch 从您在 problem 结构体中给出的起点运行 fmincon。如果此次运行收敛,GlobalSearch 将记录起点和终点,以对吸引盆的半径进行初步估计。此外,GlobalSearch 记录了最终的目标函数值,以供 score 函数使用(请参阅 获取第一阶段起点,运行)。
得分函数是某一点的目标函数值与约束违反次数和的倍数之和。因此可行点的得分等于其目标函数值。约束违反的倍数最初为 1000。GlobalSearch 在运行期间更新倍数。
生成尝试点
GlobalSearch 使用散射搜索算法生成一组 NumTrialPoints 试验点。试验点是潜在的起点。有关散射搜索算法的描述,请参阅 Glover [2]。GlobalSearch 会在您设定的任何有限边界内生成试验点(lb 和 ub)。无界分量具有强加的人为边界:lb = -1e4 + 1,ub = 1e4 + 1。该范围不关于原点对称,因此原点不在散射搜索中。具有单侧边界的组件在无界侧施加了人为边界,并通过有限边界进行移动以保持 lb < ub。
获取第一阶段起点,运行
GlobalSearch 评估一组 NumStageOnePoints 试验点的得分函数。然后,它取得分最高的点并从该点运行 fmincon。GlobalSearch 从要检查的点列表中删除 NumStageOnePoints 试验点集。
初始化盆地、计数器、阈值
localSolverThreshold 最初是解处两个目标函数值中较小的一个。解点是从 x0 和第 1 阶段起点开始的 fmincon 解。如果这两个解点都不存在或者不可行,则 localSolverThreshold 最初是第 1 阶段起点的罚函数值。
GlobalSearch 启发式假设是吸引盆是球形的。来自 x0 的解点和来自第 1 阶段的解点的吸引盆的初始估计是以解点为中心的球体。每个球体的半径是从初始点到解的距离。这些估计的盆地可以重叠。
有两组计数器与该算法相关。每个计数器是连续试验点的数量:
位于吸引力盆地内。每个盆地都有一个柜台。
得分函数大于
localSolverThreshold。有关分数的定义,请参阅从 x0 运行 fmincon。
所有计数器最初都是 0。
开始主循环
GlobalSearch 重复检查列表中剩余的试验点,并执行以下步骤。它持续监控时间,如果经过的时间超过 MaxTime 秒,则停止搜索。
检查第 2 阶段试验点以查看 fmincon 是否运行
调用试验点 p。如果满足以下条件,则从 p 运行 fmincon:
p不位于任何现有盆地中。每个盆地i的标准是:|p - center(i)| > DistanceThresholdFactor * radius(i).
DistanceThresholdFactor是一个选项(默认值为0.75)。radius是一个估计半径,在更新盆地半径和阈值和对较大计数器值做出反应时更新。score(
p) <localSolverThreshold。(可选)
p满足边界和/或不等式约束。如果将GlobalSearch对象的StartPointsToRun属性设置为'bounds'或'bounds-ineqs',则会发生此测试。
当 fmincon 运行时
重置计数器
将盆地和阈值的计数器设置为 0。
更新解集
如果
fmincon从p开始运行,它可以产生一个正的退出标志,表示收敛。在这种情况下,GlobalSearch会更新GlobalOptimSolution对象的向量。将解点称为xp,将目标函数值称为fp。有两种情况:对于每个其他解
xq,其目标函数值为fq,|xq - xp| > XTolerance * max(1,|xp|)或
|fq - fp| > FunctionTolerance * max(1,|fp|).在这种情况下,
GlobalSearch在GlobalOptimSolution对象向量中创建一个新元素。有关每个对象所包含信息的详细信息,请参阅GlobalOptimSolution。对于其他解
xq,其目标函数值为fq,|xq - xp| <= XTolerance * max(1,|xp|)和
|fq - fp| <= FunctionTolerance * max(1,|fp|).在这种情况下,
GlobalSearch将xp视为等同于xq。GlobalSearch算法通过将xq添加到p点的元胞数组中来修改X0的GlobalOptimSolution。此次更新可能会有一个小调整。如果
xq的退出标志大于1,并且xp的退出标志为1,则xp将替换xq。这种替换会导致同一盆地内某些点与XTolerance的距离超过xp。
更新盆地半径和阈值
如果当前
fmincon运行的退出标志为正:将阈值设置为起点
p处的分数值。将
xp的盆地半径设置为等于现有半径(如果有)和p与xp之间的距离中的最大值。
报告至迭代显示
当
GlobalSearchDisplay属性为'iter'时,fmincon运行的每个点都会在GlobalSearch迭代显示中创建一条线。
当 fmincon 不运行时
更新计数器
对每个包含
p的盆地增加计数器。将其他每个盆地的计数器重置为0。如果 score(
p) >=localSolverThreshold则增加阈值计数器。否则,将计数器重置为0。对较大的计数器值做出反应
对于每个计数器等于
MaxWaitCycle的盆地,将盆地半径乘以1–BasinRadiusFactor。将计数器重置为0。(MaxWaitCycle和BasinRadiusFactor都是GlobalSearch对象的可设置属性。)如果阈值计数器等于
MaxWaitCycle,则增加阈值:新阈值 = 阈值 +
PenaltyThresholdFactor*(1+ abs(阈值))。将计数器重置为
0。报告至迭代显示
每 200 个试验点在
GlobalSearch迭代显示中创建一条线。
创建 GlobalOptimSolution
在达到 MaxTime 秒或用完试验点后,GlobalSearch 会创建一个 GlobalOptimSolution 对象的向量。(这些点对应于正的 fmincon 退出标志。)GlobalSearch 按目标函数值对向量进行排序,从最低(最佳)到最高(最差)。至此,算法结束。
MultiStart 算法
当您 run 一个 MultiStart 对象时,算法执行以下步骤:
验证输入
MultiStart 检查输入参量的有效性。检查包括对问题输入运行一次局部求解器。即使并行运行,MultiStart 也会串行执行这些检查。
生成起点
如果您使用以下语法调用 MultiStart
[x,fval] = run(ms,problem,k)
对于整数 k,MultiStart 会生成 k - 1 起点,就像使用 RandomStartPointSet 对象一样。该算法还使用 x0 结体构中的 problem 起点,总共 k 个起点。
RandomStartPointSet 对象内部没有存储任何点。相反,MultiStart 调用 list,它在 problem 结构体给出的边界内生成随机点。如果存在无界分量,list 将使用 RandomStartPointSet 对象的 ArtificialBound 属性给出的人工边界。
如果您提供一个 CustomStartPointSet 对象,MultiStart 不会生成起点,而是使用对象中的点。
过滤起点(可选)
如果将 MultiStart 对象的 StartPointsToRun 属性设置为 'bounds' 或 'bounds-ineqs',则 MultiStart 不会从不可行的起点运行局部求解器。在这里,“不可行”的意思是起点不满足边界,或者起点既不满足边界也不满足不等式约束。
StartPointsToRun 的默认设置是 'all'。在这种情况下,MultiStart 不会丢弃不可行的起点。
运行本地求解器
MultiStart 运行 problem.solver 中指定的局部求解器,从通过 StartPointsToRun 过滤器的点开始。如果 MultiStart 处于并行运行状态,它会逐个向工作单元发送起始点,然后工作单元处理器运行局部求解器。
在每次迭代中,局部求解器都会检查自 MultiStart 开始计算以来是否已经过去了 MaxTime 秒。如果是这样,MultiStart 将退出该迭代而不报告解。
当局部求解器停止时,MultiStart 会存储与正的局部求解器退出标志相对应的结果并继续下一步。
报告至迭代显示. 当 MultiStart Display 属性为 'iter' 时,局部求解器运行的每个点都会在 MultiStart 迭代显示中创建一条线。
检查停止条件
当 MultiStart 用完起点时就会停止。当总运行时间超过 MaxTime 秒时,它也会停止。
创建 GlobalOptimSolution 对象
在 MultiStart 达到停止条件后,算法将创建一个 GlobalOptimSolution 对象向量(所有这些都对应于正的局部求解器退出标志),如下所示:
按目标函数值(
Fval)从低到高对局部解进行排序。对于lsqnonlin和lsqcurvefit局部求解器,目标函数是残差的范数。从最低(最佳)的
j开始循环遍历局部解Fval。找到所有满足以下条件的解
k:|Fval(k) - Fval(j)| <= FunctionTolerance*max(1,|Fval(j)|)|x(k) - x(j)| <= XTolerance*max(1,|x(j)|)记录
j、Fval(j)、output的局部求解器j结构体,以及j和所有k的起点元胞数组。从局部解列表中删除那些点k。该点是GlobalOptimSolution对象向量中的一个条目。
GlobalOptimSolution 对象的结果向量按 Fval 的顺序排列,从最低(最好)到最高(最差)。
报告至迭代显示. 在检查了所有局部解之后,MultiStart 对迭代显示进行了总结。该摘要包括局部求解器运行收敛的次数、未收敛的次数以及出现错误的次数。
参考文献
[1] Ugray, Zsolt, Leon Lasdon, John C. Plummer, Fred Glover, James Kelly, and Rafael Martí. Scatter Search and Local NLP Solvers: A Multistart Framework for Global Optimization. INFORMS Journal on Computing, Vol. 19, No. 3, 2007, pp. 328–340.
[2] Glover, F. “A template for scatter search and path relinking.” Artificial Evolution (J.-K. Hao, E.Lutton, E.Ronald, M.Schoenauer, D.Snyers, eds.). Lecture Notes in Computer Science, 1363, Springer, Berlin/Heidelberg, 1998, pp. 13–54.
[3] Dixon, L. and G. P. Szegö. “The Global Optimization Problem: an Introduction.” Towards Global Optimisation 2 (Dixon, L. C. W. and G. P. Szegö, eds.). Amsterdam, The Netherlands: North Holland, 1978.