使用 `surrogateopt` 解决可行性问题，基于问题

有些问题要求您找到一个满足所有约束的点，而没有目标函数需要最小化。例如，假设您有以下约束：

$\begin{array}{l} (y + x^{2})^{2} + 0.1 y^{2} \leq 1 \\ y \leq \exp (- x) - 3 \\ y \leq x - 4 . \end{array}$

是否有任何点 $(x, y)$ 满足约束？要回答这个问题，您需要评估各个点的表达。surrogateopt 求解器不需要您提供初始点，它会搜索广泛的点集。因此，surrogateopt 可以很好地解决可行性问题。

要可视化约束，请参阅可视化约束。有关该问题的基于求解器的方法，请参阅解决可行性问题。

注意：此示例使用了两个辅助函数，outfun 和 evaluateExpr。本示例末尾提供了每个函数的代码。确保每个函数的代码都包含在脚本的末尾或路径上的文件中。

建立可行性问题

对于基于问题的方法，创建优化变量 x 和 y，并为列出的约束创建表达式。要使用 surrogateopt 求解器，您必须为所有变量设置有限边界。设置下界为 -10，上界为 10。

x = optimvar("x","LowerBound",-10,"UpperBound",10);
y = optimvar("y","LowerBound",-10,"UpperBound",10);
cons1 = (y + x^2)^2 + 0.1*y^2 <= 1;
cons2 = y <= exp(-x) - 3;
cons3 = y <= x - 4;

创建一个优化问题并将约束包含在问题中。

prob = optimproblem("Constraints",[cons1 cons2 cons3]);

该问题没有目标函数。在内部，求解器将每个点的目标函数值设置为 0。

求解问题

使用 surrogateopt 求解问题。

rng(1) % For reproducibility
[sol,fval] = solve(prob,"Solver","surrogateopt")

Solving problem using surrogateopt.

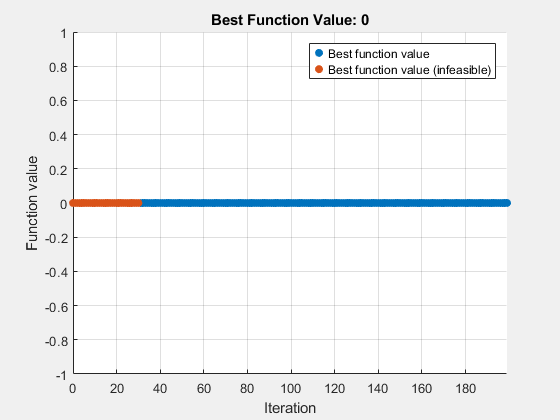
Figure Optimization Plot Function contains an axes object. The axes object with title Best Function Value: 0, xlabel Iteration, ylabel Function value contains 2 objects of type scatter. These objects represent Best function value, Best function value (infeasible).

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

sol = struct with fields:
    x: 1.7435
    y: -3.1255

fval = 
0

前几个评估点是不可行的，如图中红色所示。经过大约 60 次评估后，求解器会找到一个可行点，以蓝色绘制。

检查返回的解的可行性。

infeasibility(cons1,sol)

ans = 
0

infeasibility(cons2,sol)

ans = 
0

infeasibility(cons3,sol)

ans = 
0

所有不可行性均为零，表明点 sol 是可行的。

在第一个可行点处停止求解器

为了更快地找到解，请创建一个输出函数（请参阅输出函数），当求解器达到可行点时，它会停止求解器。此示例末尾的 outfun 辅助函数在到达没有约束违反的点时停止求解器。

使用 outfun 输出函数解决问题。

opts = optimoptions("surrogateopt","OutputFcn",@outfun);
rng(1) % For reproducibility
[sol,fval] = solve(prob,"Solver","surrogateopt","Options",opts)

Solving problem using surrogateopt.

Optimization stopped by a plot function or output function.

sol = struct with fields:
    x: 1.7435
    y: -3.1255

fval = 
0

这次，求解器比以前停止得更早。

可视化约束

为了可视化约束，使用 fimplicit 绘制每个约束函数为零的点。fimplicit 函数将数值传递给其函数，而 evaluate 函数需要一个结构体。要将这些函数绑定在一起，请使用 evaluateExpr 辅助函数，它出现在本示例的末尾。此函数只是将传递的值放入具有适当名称的结构体中。

避免由于 evaluateExpr 函数不适用于向量化输入而出现警告。将返回的解点绘制为绿色圆圈。

s = warning('off','MATLAB:fplot:NotVectorized');
figure
cc1 = (y + x^2)^2 + 0.1*y^2 - 1;
fimplicit(@(a,b)evaluateExpr(cc1,a,b),[-2 2 -4 2],'r')
hold on
cc2 = y - exp(-x) + 3;
fimplicit(@(a,b)evaluateExpr(cc2,a,b),[-2 2 -4 2],'k')
cc3 = y - x + 4;
fimplicit(@(x,y)evaluateExpr(cc3,x,y),[-2 2 -4 2],'b')
plot(sol.x,sol.y,'og')
hold off

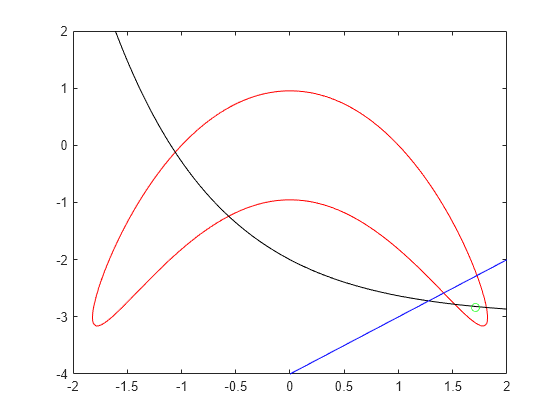
Figure contains an axes object. The axes object contains 4 objects of type implicitfunctionline, line. One or more of the lines displays its values using only markers

warning(s);

可行区域位于红色轮廓内、黑线和蓝线下方。可行区域位于红色轮廓的右下方。

辅助函数

以下代码创建 outfun 辅助函数。

function stop = outfun(~,optimValues,state)
stop = false;
switch state
    case 'iter'
        if optimValues.currentConstrviolation <= 0
            stop = true;
        end
end
end

以下代码创建 evaluateExpr 辅助函数。

function p = evaluateExpr(expr,x,y)
pt.x = x;
pt.y = y;
p = evaluate(expr,pt);
end

另请参阅

solve | infeasibility | surrogateopt

使用 surrogateopt 解决可行性问题，基于问题