Use Buses to Improve Readability of Model and Generate HDL Code
You can follow these guidelines to learn about buses, how to model your design by using buses, and generate HDL code. Each guideline has a severity level that indicates the level of compliance requirements. To learn more, see HDL Modeling Guidelines Severity Levels.
Guideline ID
1.3.3
Severity
Informative
Description
When to Use Buses?
If your DUT or other blocks in your model have many input or output signals, you can create buses to improve the readability of your model. A bus is a composite signal that consists of other signals that are called elements. The bus can have a structure of different data types or a vector signal with the same data types. The constituent signals or elements of a bus can be:
Mixed data type signals such as double, integer, and fixed-point
Mixed scalar and vector elements
Mixed real and complex signals
Other buses nested to any level
Multidimensional signals
HDL Coder Support for Buses
You can generate HDL code for designs that have:
DUT subsystem ports connected to buses.
Simulink® and Stateflow® blocks supported for HDL code generation.
HDL Coder™ supports code generation for bus-capable blocks in the HDL Coder block library. Bus-capable blocks are blocks that can accept buses as input and produce buses as outputs. For a list of bus-capable blocks that Simulink supports, see Bus-Capable Blocks.
See Signal and Data Type Support for blocks that support HDL code generation with buses.
Create Buses
You can create buses by using Bus Creator blocks. A Bus Creator block assigns a name to each element of the created bus. You can then refer to elements by name when you search for their sources.
For an example that illustrates how to model with buses, open hdlcoder_bus_nested.slx. Double-click the HDL_DUT Subsystem.
open_system('hdlcoder_bus_nested') set_param('hdlcoder_bus_nested','SimulationCommand','Update') open_system('hdlcoder_bus_nested/HDL_DUT')
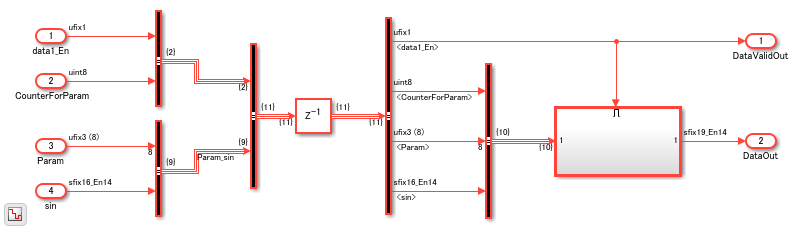
In this model, the Bus Creator blocks create two buses. One bus contains data1_En and CounterForParam signals. The other bus contains Param and sin signals. By default, each signal of the bus inherits the name of the signal connected to the bus.
Nest Buses
You see another Bus Creator block that combines these two buses. When one or more inputs to a Bus Creator block is a bus, the output is a nested bus.
The Bus Creator block generates names for buses whose corresponding inputs do not have names. The names are in the form signaln, where n is the number of the port the input signal connects to. For example, if you open the Block Parameters dialog box for the second Bus Creator block, you see Elements in the bus as signal1 and Param_sin.
Assign Signal Values to Bus
To change bus element values, use a Bus Assignment block. Use a Bus Assignment block to change bus element values without adding Bus Selector and Bus Creator blocks that select bus elements and reassemble them into a bus.
For example, open the model hdlcoder_bus_nested_assignment.
open_system('hdlcoder_bus_nested_assignment') set_param('hdlcoder_bus_nested_assignment','SimulationCommand','Update') open_system('hdlcoder_bus_nested_assignment/HDL_DUT')
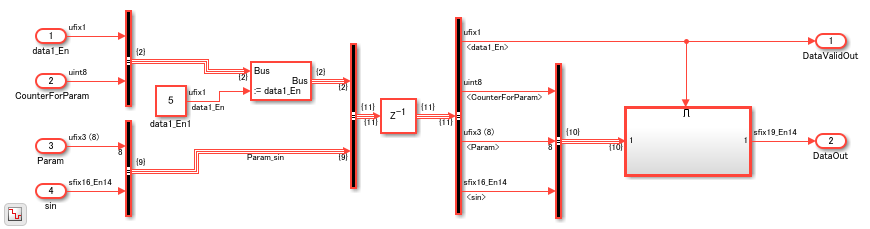
In the model, you see a Bus Assignment block that assigns the value 5 to the data1_En signal in the bus.
Select Bus Outputs
To extract the signals from a bus that includes nested buses, use Bus Selector blocks. By default, the block outputs the specified bus elements as separate signals. You can also output the signals as another bus. You can use the OutputSignals block property to see the Elements in the bus that the block outputs. By using this property, you can track which signals are entering a Bus Selector block deep within your model hierarchy.
get_param('hdlcoder_bus_nested/HDL_DUT/Bus Selector5', 'OutputSignals')
ans =
'signal1.data1_En,signal1.CounterForParam,Param_sin.Param,Param_sin.sin'
Generate HDL Code
To generate HDL code for this model, run this command:
makehdl('hdlcoder_bus_nested/HDL_DUT')
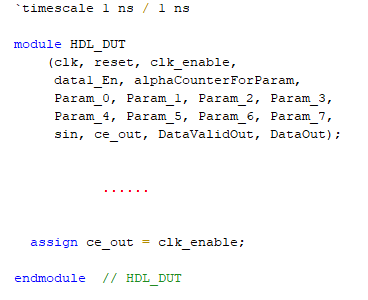
You see that the code generator expands the buses to scalar signals in the generated code. For example, if you open the generated Verilog file for the HDL_DUT Subsystem, for the Delay block that takes the two nested buses signal1 and Param_sin, you see four always blocks created for each signal in the bus. For example, you see an always block for the data1_En signal that is part of signal1. This figure displays the scalar signals created for each bus in the module definition.
Simplify Subsystem Bus Interfaces
You can simplify the Subsystem bus interfaces by using Bus Element blocks. The In Bus Element and Out Bus Element blocks provide a simplified and flexible way to use buses as inputs and outputs to subsystems. The In Bus Element block is equivalent to an Inport block combined with a Bus Selector block. The Out Bus Element block is equivalent to an Outport block combined with a Bus Creator block. To refactor an existing model that uses Inport, Bus Selector, Bus Creator, and Outport blocks to use In Bus Element and Out Bus Element blocks, you can use Simulink Editor action bars.
For example, open the model hdlcoder_bus_nested_simplified. This model is functionally equivalent to the hdlcoder_bus_nested model but is a more simplified version.
open_system('hdlcoder_bus_nested_simplified') set_param('hdlcoder_bus_nested_simplified','SimulationCommand','Update') open_system('hdlcoder_bus_nested_simplified/HDL_DUT')
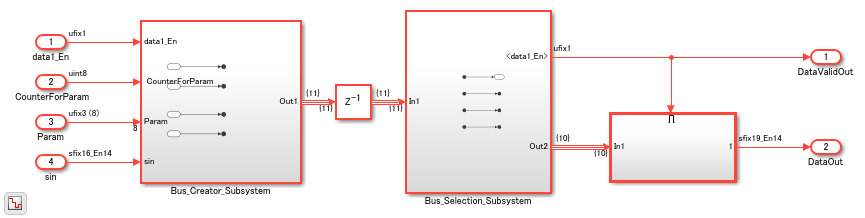
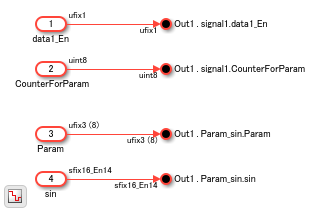
The model has two Subsystems that perform bus creation and bus selection by using Bus Element blocks. The Bus_Creator_Subsystem combines the Outport blocks with the Bus Creator blocks to create Out Bus Element blocks.
open_system('hdlcoder_bus_nested_simplified/HDL_DUT/Bus_Creator_Subsystem')
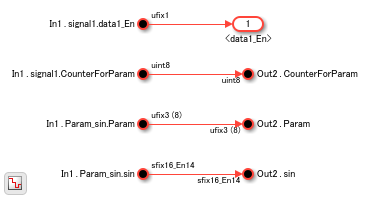
The Bus_Selection_Subsystem combines the Inport blocks with the Bus Selector blocks to create In Bus Element blocks.
open_system('hdlcoder_bus_nested_simplified/HDL_DUT/Bus_Selection_Subsystem')
To learn more, see Simplify Subsystem and Model Interfaces with Bus Element Ports.
Virtual and Nonvirtual Buses
The buses in the model hdlcoder_bus_nested created earlier by using Bus Creator and Bus Selector blocks are virtual buses. Each bus element is stored in memory, but the bus is not stored. The bus simplifies the graph but has no functional effect. In the generated HDL code, you see the constituent signals but not the bus.
To more easily track the correspondence between a bus in the model and the generated HDL code, use nonvirtual buses. Nonvirtual buses generate clean HDL code because it uses a structure to hold the buses. To convert a virtual bus to a nonvirtual bus, in the Block Parameters of the Bus Creator blocks, you specify the Output data type as Bus: object_name by replacing object_name with the name of the bus object and then select Output as nonvirtual bus.
See Convert Virtual Bus to Nonvirtual Bus.
Array of Buses
An array of buses is an array whose elements are buses. Each element in an array of buses must be nonvirtual and must have the same data type.
To learn more about modeling with array of buses, see Generating HDL Code for Subsystems with Array of Buses.