Control Point Registration
Control point registration, or point mapping, enables you to register two images based on corresponding features that you manually select from the two images. One image, called the fixed image, is a reference image in the desired orientation. The other image, called the moving image, is the image that you want to align to the reference image. Control points are pairs of points that identify the same features or landmarks in the fixed and moving images. Control point registration consists of these steps:
Select pairs of control points in the fixed and moving images.
Optionally, fine-tune control point placement automatically after you select the control points.
Estimate the geometric transformation from the positions of the control points.
Apply the geometric transformation to the moving image, resulting in an image that is aligned with the fixed image.
The figure provides an illustration of this process. See Register Images with Projection Distortion Using Control Points for an extended example.
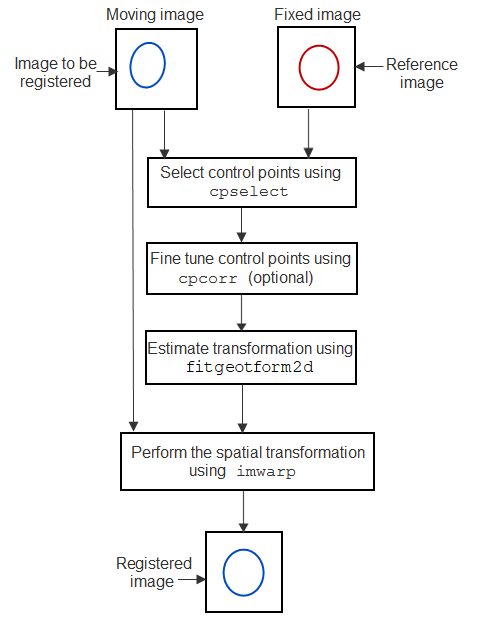
You may need to perform several iterations of this process, experimenting with different types of transformations, before you achieve a satisfactory result. Sometimes, you can perform successive registrations, removing gross global distortions first, and then removing smaller local distortions in subsequent passes.
Select Pairs of Control Points
To select control points in a pair of 2-D images interactively, use the Control Point
Selection tool. Open the tool by using the cpselect function. The figure shows the default appearance of the tool when
you first start it, with the moving image on the left and the fixed image on the
right.

Select control points by pointing and clicking in the moving and fixed images, in either the Detail or the Overview windows. Each point you specify in the moving image must have a match in the fixed image. For more information, see Select Matching Control Point Pairs.
To save control points to the workspace, select File on the Control Point Selection tool menu bar, then choose the Export Points to Workspace option. The control points are now available for the next steps in image registration.
Fine-Tune Control Point Placement
You can fine-tune the position of the 2-D control points by using cross-correlation. To
use cross-correlation, pass sets of control points in the moving and fixed images, along
with the images themselves, to the cpcorr function.
The cpcorr function defines 11-by-11 pixel regions around each
control point in the moving image and around the matching control point in the fixed image.
The function then calculates the correlation between the values at each pixel in the region.
Next, the cpcorr function finds the position with the highest
correlation value and uses it as the optimal position of the control point. The function
only moves control points up to four pixels based on the results of the
cross-correlation.
Note
Features in the two images must be at the same scale and have the same orientation. They cannot be rotated relative to each other.
If cpcorr cannot correlate some of the control points, it returns
their unmodified values in movingPoints.
Estimate the Geometric Transformation
The fitgeotform2d
function can infer the parameters from control point pairs for the following types of
geometric transformations, listed in order of complexity. The function returns a geometric
transformation object that stores the parameters for applying the transformation to an
image.
Transformation Type | Description | Minimum Number of Control Point Pairs | Example |
|---|---|---|---|
"similarity" | Use this transformation when shapes in the moving image are unchanged, but the image is distorted by some combination of translation, rotation, and isotropic scaling. Straight lines remain straight, and parallel lines are still parallel. | 2 |
|
"reflectivesimilarity" | Same as "similarity" with the addition of optional
reflection. | 3 |
|
"affine" | Use this transformation when shapes in the moving image exhibit shearing. Straight lines remain straight, and parallel lines remain parallel, but rectangles become parallelograms. | 3 |
|
"projective" | Use this transformation when the scene appears tilted. Straight lines remain straight, but parallel lines converge toward a vanishing point. | 4 |
|
"polynomial" | Use this transformation when objects in the image are curved. The higher the order of the polynomial, the better the fit, but the result can contain more curves than the fixed image. | 6 (order 2) 10 (order 3) 15 (order 4) |
|
"pwl" | Use this transformation (piecewise linear) when parts of the image appear distorted differently. | 4 |
|
"lwm" | Use this transformation (local weighted mean), when the distortion varies locally and piecewise linear is not sufficient. | 6 (12 recommended) |
|
Your choice of transformation type affects the number of control point pairs you must
select. For example, a similarity transformation without reflection requires at least two
control point pairs. A fourth order polynomial transformation requires 15 control point
pairs. For more information about these transformation types, and the special syntaxes they
require, see cpselect.
To learn about 3-D point mapping, see fitgeotform3d (Medical Imaging Toolbox).
Apply the Geometric Transformation
Use the imwarp function to apply the geometric
transformation to the moving image. The imwarp function returns a
version of the moving image that is registered to the fixed image.
See Also
cpselect | cpcorr | fitgeotform2d | fitgeotform3d (Medical Imaging Toolbox) | imwarp

