几何变换的矩阵表示
您可以将线性几何变换表示为数值矩阵。每种类型的变换,如平移、缩放、旋转和翻转,都是使用矩阵定义的,矩阵的元素遵循特定的模式。您可以通过合成表示变换的矩阵来组合多个变换。有关详细信息,请参阅Create Composite 2-D Affine Transformations。
二维仿射变换
下表列出了二维仿射变换以及用于定义它们的变换矩阵。对于二维仿射变换,最后一行必须为 [0 0 1]。
使用二维平移矩阵的组合来创建一个表示平移变换的
transltform2d对象。使用二维平移和旋转矩阵的组合来创建一个表示非翻转刚性变换的
rigidtform2d对象。使用二维平移、旋转和缩放矩阵的组合来创建一个表示非翻转相似变换的
simtform2d对象。使用二维变换矩阵的任意组合来创建一个表示一般仿射变换的
affinetform2d对象。
| 二维仿射变换 | 示例(原始图像和变换后的图像) | 变换矩阵 | |
|---|---|---|---|
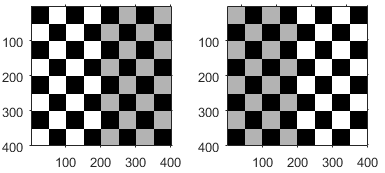
| 平移 |
| tx 指定沿 x 轴的位移 ty 指定沿 y 轴的位移。 有关像素坐标的详细信息,请参阅图像坐标系。 | |
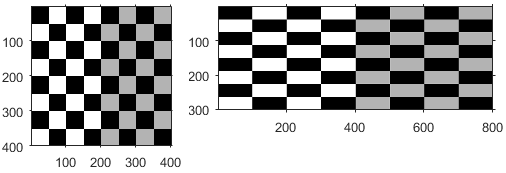
| 缩放 | | sx 指定沿 x 轴的缩放因子 sy 指定沿 y 轴的缩放因子。 | |
| 剪切 | | shx 指定沿 x 轴的剪切因子。 shy 指定沿 y 轴的剪切因子。 | |
| 翻转 |
| φ 指定翻转轴的角度,以度为单位。 两种常见的翻转为垂直翻转和水平翻转。垂直翻转是围绕 x 轴的翻转,因此 φ 为 0,翻转矩阵简化为:
水平翻转是围绕 y 轴的翻转,因此 φ 为 90,翻转矩阵简化为:
| |
| 旋转 | | θ 指定围绕原点的旋转角度(以度为单位)。 | |
二维投影变换
投影变换使图像平面倾斜。平行线可以向一个消失点收敛,形成深度的外观。
变换矩阵是一个 3×3 矩阵。与仿射变换不同,变换矩阵的最后一行没有限制。使用二维仿射和投影变换矩阵的任意组合来创建表示一般投影变换的 projtform2d 对象。
| 二维投影变换 | 示例 | 变换矩阵 | |
|---|---|---|---|
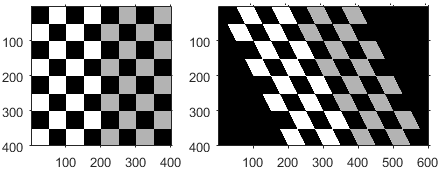
| 倾斜 |
|
| E 和 F 对消失点有影响。 当 E 和 F 较大时,消失点更接近原点,因此平行线似乎收敛得更快。 |
三维仿射变换
下表列出了三维仿射变换以及用于定义它们的变换矩阵。请注意,在三维情况下具有多个矩阵,具体取决于您要如何旋转或剪切图像。对于三维仿射变换,最后一行必须为 [0 0 0 1]。
使用三维平移矩阵的组合来创建一个表示平移变换的
transltform3d对象。使用三维平移和旋转矩阵的组合来创建一个表示非翻转刚性变换的
rigidtform3d对象。使用三维平移、旋转和缩放矩阵的组合来创建一个表示非翻转相似变换的
simtform3d对象。使用三维变换矩阵的任意组合来创建一个表示一般仿射变换的
affinetform3d对象。
| 三维仿射变换 | 变换矩阵 | ||
|---|---|---|---|
| 平移 | 在 x、y 和 z 方向分别按量 tx、ty 和 tz 进行平移:
| ||
| 缩放 | 在 x、y 和 z 维度中,分别按缩放因子 sx、sy 和 sz 进行缩放:
| ||
| 剪切 | 在 y-z 平面内剪切:
使得
| 在 x-z 平面内剪切:
使得
| 在 x-y 平面内剪切:
使得
|
| 翻转 | 穿过 y-z 平面的翻转,对 x 坐标求反:
| 穿过 x-z 平面的翻转,对 y 坐标求反:
| 穿过 x-y 平面的翻转,对 z 坐标求反:
|
| 旋转 | 在 y-z 平面内围绕 x 轴旋转角度 θx(以度为单位):
| 在 x-z 平面内绕 y 轴旋转角度 θy(以度为单位):
| 在 x-y 平面内绕 z 轴旋转角度 θz(以度为单位):
|
三维投影变换和 N 维变换
imwarp 函数不支持三维投影变换或 N 维仿射和投影变换。不过,您可以使用 maketform 函数从几何变换矩阵创建空间变换结构体。然后,使用 tformarray 函数将变换应用于图像。有关详细信息,请参阅N-Dimensional Spatial Transformations。
变换矩阵的维数必须为 (N+1)×(N+1)。maketform 和 tformarray 函数使用后乘矩阵约定。后乘约定中的几何变换矩阵是前乘约定中矩阵的转置。因此,对于 N 维仿射变换矩阵,最后一列必须包含 [zeros(N,1); 1],对最后一行的值没有限制。
另请参阅
imwarp | fitgeotform2d | affinetform2d | affinetform3d | projtform2d