ns3

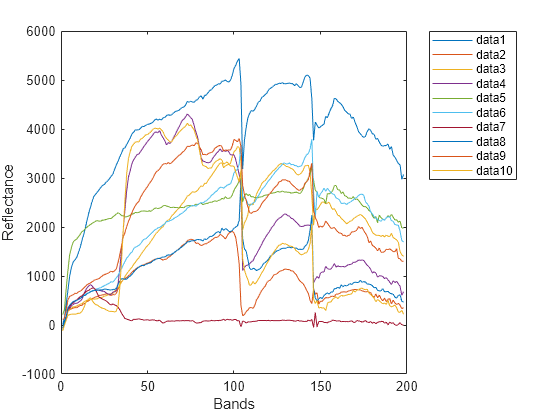
Measure normalized spectral similarity score

Since R2020b

Syntax

score = ns3(inputData,refSpectrum)

score = ns3(testSpectrum,refSpectrum)

Description

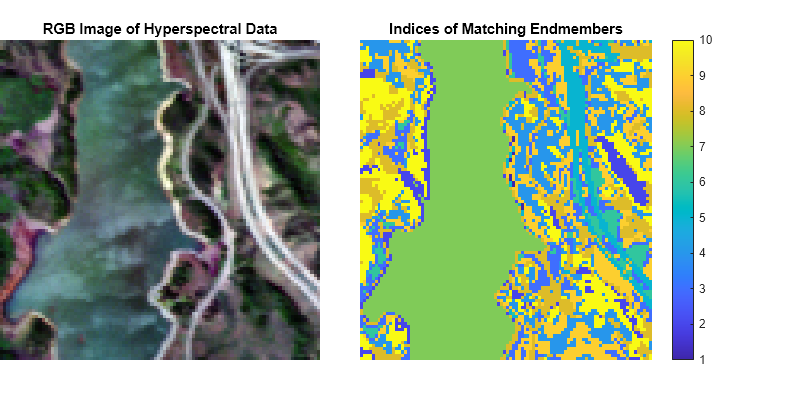
score = ns3(inputData,refSpectrum) measures the spectral similarity between the spectrum of each pixel in the hyperspectral data inputData and the specified reference spectrum refSpectrum by using the normalized spectral similarity score (NS3) method. Use this syntax to identify different regions or materials in a hyperspectral data cube. For information about the NS3 method, see More About.

example

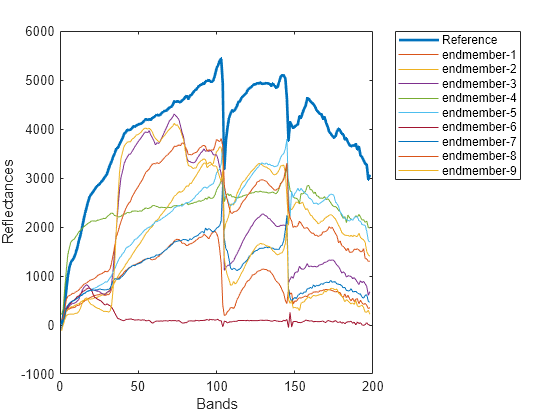
score = ns3(testSpectrum,refSpectrum) measures the spectral similarity between the specified test spectrum testSpectrum and reference spectrum refSpectrum by using the NS3 method. Use this syntax to compare the spectral signature of an unknown material against the reference spectrum or to compute spectral variability between two spectral signatures.

Note

This function requires the Hyperspectral Imaging Library for Image Processing Toolbox™. You can install the Hyperspectral Imaging Library for Image Processing Toolbox from Add-On Explorer. For more information about installing add-ons, see Get and Manage Add-Ons.

The Hyperspectral Imaging Library for Image Processing Toolbox requires desktop MATLAB^®, as MATLAB Online™ or MATLAB Mobile™ do not support the library.

example

Examples

collapse all

Distinguish Hyperspectral Regions Using NS3 Measure

This example uses:

Hyperspectral Imaging Library for Image Processing Toolbox Hyperspectral Imaging Library for Image Processing Toolbox

Open Live Script

Read hyperspectral data into the workspace.

hcube = hypercube('jasperRidge2_R198.hdr');

Estimate the number of spectrally distinct endmembers in the data cube by using countEndmembersHFC function.

numEndmembers = countEndmembersHFC(hcube,'PFA',10^-7);

Extract the endmember spectral signatures from the data cube by using the NFINDR algorithm.

endmembers = nfindr(hcube,numEndmembers);

Plot the spectral signatures of the extracted endmembers.

figure
plot(endmembers)
xlabel('Bands')
ylabel('Reflectance')
legend('Location','Bestoutside')

Figure contains an axes object. The axes object with xlabel Bands, ylabel Reflectance contains 10 objects of type line.

Compute the NS3 distance between each endmember and the spectrum of each pixel in the data cube.

score = zeros(size(hcube.DataCube,1),size(hcube.DataCube,2),numEndmembers);
for i = 1:numEndmembers
    score(:,:,i) = ns3(hcube,endmembers(:,i));
end

Compute the minimum score value from the distance scores obtained for each pixel spectrum with respect to all the endmembers. The index of each minimum score identifies the endmember spectrum to which a pixel spectrum exhibits maximum similarity. An index value, n, at the spatial location (x, y) in the score matrix indicates that the spectral signature of the pixel at spatial location (x, y) in the data cube best matches the spectral signature of the nth endmember.

[~,matchingIdx] = min(score,[],3);

Estimate an RGB image of the input data by using the colorize function.

rgbImg = colorize(hcube,'Method','rgb','ContrastStretching',true);

Display both the RGB image and the matrix of matched index values.

figure('Position',[0 0 800 400])
subplot('Position',[0 0.1 0.4 0.8])
imagesc(rgbImg)
axis off
title('RGB Image of Hyperspectral Data')
subplot('Position',[0.45 0.1 0.45 0.8])
imagesc(matchingIdx)
axis off
title('Indices of Matching Endmembers')
colorbar

Figure contains 2 axes objects. Hidden axes object 1 with title RGB Image of Hyperspectral Data contains an object of type image. Hidden axes object 2 with title Indices of Matching Endmembers contains an object of type image.

Determine Similarity of Endmember Spectra Using NS3

This example uses:

Hyperspectral Imaging Library for Image Processing Toolbox Hyperspectral Imaging Library for Image Processing Toolbox

Open Live Script

Read hyperspectral data into the workspace.

hcube = hypercube('jasperRidge2_R198.hdr');

Find the first 10 endmembers of the hyperspectral data.

numEndmembers = 10;
endmembers = nfindr(hcube,numEndmembers);

Consider the first endmember as the reference spectrum and the rest of the endmembers as the test spectrum.

refSpectrum = endmembers(:,1);
testSpectra = endmembers(:,2:end);

Plot the reference spectrum and other endmember spectra.

figure
plot(refSpectrum,'LineWidth',2)
hold on
plot(testSpectra)
hold off
label = cell(1,numEndmembers-1);
label{1} = 'Reference';
for itr = 1:numEndmembers-1
    label{itr+1} = ['endmember-' num2str(itr)];
end
xlabel('Bands')
ylabel('Reflectances')
legend(label,'Location','Bestoutside')

Figure contains an axes object. The axes object with xlabel Bands, ylabel Reflectances contains 10 objects of type line. These objects represent Reference, endmember-1, endmember-2, endmember-3, endmember-4, endmember-5, endmember-6, endmember-7, endmember-8, endmember-9.

Compute the NS3 score between the reference and test spectra.

score = zeros(1,numEndmembers-1);
for itr = 1:numEndmembers-1
    score(itr) = ns3(testSpectra(:,itr),refSpectrum);
end

Find the test spectrum that exhibit maximum similarity (minimum distance) to the reference spectrum. Then, find the test spectrum that exhibit minimum similarity (maximum distance) to the reference spectrum.

[minval,minidx] = min(score);
maxMatch = testSpectra(:,minidx);
[maxval,maxidx] = max(score);
minMatch = testSpectra(:,maxidx);

Plot the reference spectrum, the maximum similarity, and the minimum similarity test spectrum. The test spectrum with the minimum score value indicates highest similarity to the reference endmember. On the other hand, the test spectrum with the maximum score value has the highest spectral variability.

figure
plot(refSpectrum,'LineWidth',2)
hold on
plot(maxMatch,'k')
plot(minMatch,'r')
xlabel('Band Number')
ylabel('Data Values')
legend('Reference spectrum','Maximum match test spectrum','Minimum match test spectrum',...
       'Location','Southoutside')
title('Similarity Between Spectra')
text(40,500,['Max score: ' num2str(maxval)],'Color','r')
text(120,1900,['Min score: ' num2str(minval)],'Color','k')

Figure contains an axes object. The axes object with title Similarity Between Spectra, xlabel Band Number, ylabel Data Values contains 5 objects of type line, text. These objects represent Reference spectrum, Maximum match test spectrum, Minimum match test spectrum.

Input Arguments

collapse all

`inputData` — Input hyperspectral data
`hypercube` object | 3-D numeric array

Input hyperspectral data, specified as a hypercube object or a 3-D numeric array containing the data cube. If the input is a hypercube object, the data is read from the DataCube property of the object.

`testSpectrum` — Test spectrum
C-element vector

Test spectrum, specified as a C-element vector. The test spectrum is the spectral signature of an unknown region or material.

`refSpectrum` — Reference spectrum
C-element vector

Reference spectrum, specified as a C-element vector. The reference spectrum is the spectral signature of a known region or material. The function matches the test spectrum against these values.

Output Arguments

collapse all

`score` — NS3 score
scalar | matrix

NS3 score, returned as a scalar or matrix. The output is a

scalar — If you specify the testSpectrum input argument. The function matches the test spectral signature against the reference spectral signature and returns a scalar value. Both the test and the reference spectra must be vectors of same length.
matrix — If you specify the inputData input argument. The function matches the spectral signature of each pixel in the data cube against the reference spectral signature and returns a matrix. If the data cube is of size M-by-N-by-C and the reference spectrum is a vector of length C, the output matrix is of size M-by-N.

A smaller NS3 score indicates a strong match between the test signature and the reference signature.

Data Types: single | double

Limitations

This function does not support parfor loops, as its performance is already optimized. (since R2023a)

More About

collapse all

Normalized Spectral Similarity Score (NS3)

The NS3 method computes spectral similarity based on the Euclidean and SAM distances between two spectra. Let r and t be the reference and test spectra respectively. Compute the Euclidean distance between two spectra as:

$A_{E u c l i d e a n} = \sqrt{\frac{1}{C} \sum_{i = 1}^{C} {(t_{i} - r_{i})}^{2}}$

Then, compute the SAM value α

$α = \cos^{- 1} (\frac{\sum_{i = 1}^{C} t_{i} r_{i}}{\sqrt{\sum_{i = 1}^{C} t_{i}^{2}} \sqrt{\sum_{i = 1}^{C} r_{i}^{2}}}) .$

Finally, compute the NS3 score as:

$N S 3 = \sqrt{A_{E u c l i d e a n}^{2} + {(1 - \cos (α))}^{2}}$

References

[1] Nidamanuri, Rama Rao, and Bernd Zbell. “Normalized Spectral Similarity Score (NS³) as an Efficient Spectral Library Searching Method for Hyperspectral Image Classification.” IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 4, no. 1 (March 2011): 226–40. https://doi.org/10.1109/JSTARS.2010.2086435.

Version History

Introduced in R2020b

ns3

Syntax

Description

Examples

Distinguish Hyperspectral Regions Using NS3 Measure

Determine Similarity of Endmember Spectra Using NS3

Input Arguments

inputData — Input hyperspectral data hypercube object | 3-D numeric array

testSpectrum — Test spectrum C-element vector

refSpectrum — Reference spectrum C-element vector

Output Arguments

score — NS3 score scalar | matrix

Limitations

More About

Normalized Spectral Similarity Score (NS3)

References

Version History

See Also

`inputData` — Input hyperspectral data
`hypercube` object | 3-D numeric array

`testSpectrum` — Test spectrum
C-element vector

`refSpectrum` — Reference spectrum
C-element vector

`score` — NS3 score
scalar | matrix