线性回归
简介
数据模型明确描述预测变量与响应变量之间的关系。线性回归拟合模型系数为线性的数据模型。最常见的线性回归类型是最小二乘拟合,它可用于拟合线和多项式以及其他线性模型。
在对各对数量之间的关系进行建模之前,最好进行相关性分析,以确定这些数量之间是否存在线性关系。请注意,变量可能具有非线性关系,相关性分析无法检测到这一点。有关详细信息,请参阅线性相关性。
MATLAB® 基本拟合用户界面可帮助您拟合数据,以便根据数据计算模型系数和绘制模型。有关示例,请参阅示例:使用基本拟合用户界面。您还可以使用 MATLAB polyfit 和 polyval 函数将您的数据拟合至具有线性系数的模型。有关示例,请参阅以编程方式拟合。
如果您需要使用非线性模型拟合数据,请转换变量以使关系变成线性关系。或者,尝试使用 Statistics and Machine Learning Toolbox™ nlinfit 函数、Optimization Toolbox™ lsqcurvefit 函数或应用 Curve Fitting Toolbox™ 中的函数,直接拟合非线性函数。
本主题解释如何:
使用
\运算符执行简单的线性回归。使用相关性分析确定两个数量之间是否相关,从而确定其是否适合进行数据拟合。
对数据进行线性模型拟合。
通过绘制残差及探索模式,评估拟合优度。
计算拟合 R2 和调整 R2 的优度测度。
简单线性回归
此示例说明如何使用 accidents 数据集执行简单线性回归。此示例还向您说明如何计算决定系数 以评估回归。accidents 数据集包含美国重大交通事故的数据。
线性回归对一个因变量(即响应变量) 与一个或多个自变量(即预测变量) 之间的关系进行建模。简单线性回归使用以下关系方程,仅考虑一个自变量:
其中, 是 y 轴截距, 是斜率(即回归系数), 是误差项。
首先确定一组( 个) 和 的观测值,以 , , ..., 形式给出。对这些值应用简单线性回归关系方程,构成一个线性系统。这些方程以矩阵形式表示如下:
假设
现在关系变为 。
在 MATLAB 中,您可使用 mldivide 运算符求 ,即 B = X\Y。
从数据集 accidents 中将事故数据加载到 y 中,将州人口数据加载到 x 中。使用 \ 运算符求州事故数量与州人口之间的线性回归关系 。\ 运算符执行最小二乘回归。
load accidents x = hwydata(:,14); %Population of states y = hwydata(:,4); %Accidents per state format long b1 = x\y
b1 =
1.372716735564871e-04
b1 是斜率或回归系数。线性关系为 。
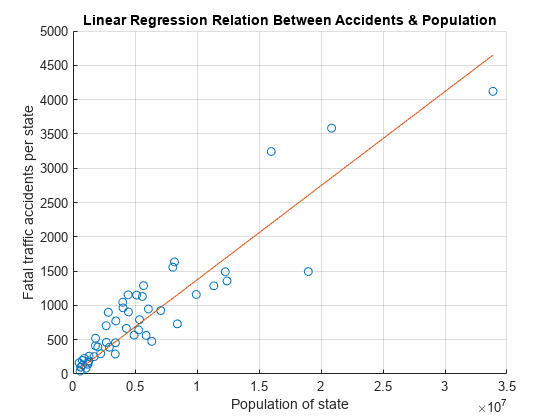
使用该关系,根据 x 计算每州的事故数量 yCalc。对实际值 y 与计算值 yCalc 进行绘图,显示回归情况。
yCalc1 = b1*x; scatter(x,y) hold on plot(x,yCalc1) xlabel('Population of state') ylabel('Fatal traffic accidents per state') title('Linear Regression Relation Between Accidents & Population') grid on
在您的模型中纳入 y 轴截距 以改进拟合,即 。用一列 1 填补 x 并使用 \ 运算符计算 。
X = [ones(length(x),1) x]; b = X\y
b = 2×1
102 ×
1.427120171726538
0.000001256394274
此结果表示关系 。
在同一幅图上绘制该结果,以图窗方式显示该关系。
yCalc2 = X*b; plot(x,yCalc2,'--') legend('Data','Slope','Slope & Intercept','Location','best');
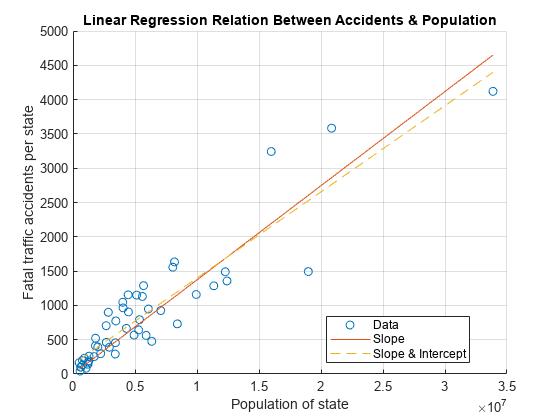
如图所示,两个拟合非常相似。探索更佳拟合的一种方法是计算决定系数 。 用于测量模型能够在多大程度上预测数据,其值介于 和 之间。 的值越高,模型预测数据的准确性越高。
其中, 表示 的计算值, 是 的均值, 定义为
通过比较 的值,找出两个拟合中较好的一个。如 值所示,包含 y 轴截距的第二个拟合更好。
Rsq1 = 1 - sum((y - yCalc1).^2)/sum((y - mean(y)).^2)
Rsq1 = 0.822235650485566
Rsq2 = 1 - sum((y - yCalc2).^2)/sum((y - mean(y)).^2)
Rsq2 = 0.838210531103428
残差与拟合优度
残差是响应变量(因变量)的观测值与模型的预测值之间的差。当拟合的模型适合数据时,残差接近独立随机误差。即,残差分布不应该呈现出可辨识的模式。
利用线性模型产生拟合需要尽量减小残差平方和。该最小化的结果即为最小二乘拟合。您可通过直观地观察残差图,了解拟合的“优度”。如果残差图具有一定的模式(即残差数据点未呈现随机分布),该随机性表明该模型并未适当地拟合数据。
评估您对数据进行的每个拟合。例如,如果您拟合数据的目的是提取具有物理含义的系数,则必须确保您的模型能够反映数据的物理属性。了解您的数据代表着什么、如何测量以及如何建模在评估拟合优度时非常重要。
拟合优度的一个测度是决定系数或 R2(读作 R 的平方)。该统计量表明您通过拟合模型得到的值与模型可预测的因变量的匹配程度。统计人员通常利用拟合模型的残差方差定义 R2:
R2 = 1 – SSresid / SStotal
SSresid 是与回归的残差的平方和。SStotal 是与因变量均值的差的平方和(总平方和)。两者都是正标量。
若要了解在使用基本拟合工具时如何计算 R2,请参阅R2,决定系数。若要了解关于计算 R2 统计量及其多元概化的更多信息,请继续阅读此处的内容。
示例:通过多项式拟合计算 R2
您可以从多项式回归的系数得出 R2,以确定线性模型对 y 的方差的解释率,如以下示例所述:
从数据文件
count.dat中count变量的前两列创建两个变量x和y:load count.dat x = count(:,1); y = count(:,2);
利用
polyfit计算从x预测y的线性回归:p = polyfit(x,y,1) p = 1.5229 -2.1911p(1)是斜率,p(2)是线性预测变量的截距。您还可以使用基本拟合用户界面获得回归系数。调用
polyval以使用p预测y,调用结果yfit:yfit = polyval(p,x);
使用
polyval,您无需自行输入拟合方程,在本例中拟合方程为:yfit = p(1) * x + p(2);
将残差值计算为有符号数的向量:
yresid = y - yfit;
计算残差的平方并相加,以获得残差平方和:
SSresid = sum(yresid.^2);
通过将观测次数减
1再乘以y的方差,计算y的总平方和:SStotal = (length(y)-1) * var(y);
利用本主题简介部分给出的公式计算 R2:
这表明,线性方程rsq = 1 - SSresid/SStotal rsq = 0.87071.5229 * x -2.1911可预测变量y中方差的 87%。
计算多项式回归的调整 R2
您通常可通过拟合更高次多项式,减少模型中的残差。当您添加更多项时,会增加决定系数 R2。您可获得更接近数据的拟合,但代价是模型更为复杂,R2 无法解释。因而,作为对该统计量的改进,调整 R2 中包括了一项对模型中项数的罚值。因此,调整 R2 更适合比较不同的模型对同一数据的拟合程度。调整 R2 定义如下:
R2adjusted = 1 - (SSresid / SStotal)*((n-1)/(n-d-1))
以下示例重复上一示例示例:通过多项式拟合计算 R2的步骤,但进行三次(3 阶)拟合而非线性(1 阶)拟合。通过三次拟合,您可同时计算简单的和调整 R2 值,以评估额外的项是否可改善预测能力:
从数据文件
count.dat中count变量的前两列创建两个变量x和y:load count.dat x = count(:,1); y = count(:,2);
调用
polyfit生成三次拟合,以从x预测y:p = polyfit(x,y,3) p = -0.0003 0.0390 0.2233 6.2779
p(4)是三次预测变量的截距。您还可以使用基本拟合用户界面获得回归系数。调用
polyval以使用p中的系数预测y,将结果命名为yfit:yfit = polyval(p,x);
polyval计算显式方程,手动输入则如下所示:yfit = p(1) * x.^3 + p(2) * x.^2 + p(3) * x + p(4);
将残差值计算为有符号数的向量:
yresid = y - yfit;
计算残差的平方并相加,以获得残差平方和:
SSresid = sum(yresid.^2);
通过将观测次数减
1再乘以y的方差,计算y的总平方和:SStotal = (length(y)-1) * var(y);
利用本主题简介部分给出的公式计算三次拟合的简单 R2:
rsq = 1 - SSresid/SStotal rsq = 0.9083最后,计算调整 R2 以解释自由度:
调整 R2 (0.8945) 小于简单 R2 (0.9083)。后者可以更可靠地估计多项式模型的预测能力。rsq_adj = 1 - SSresid/SStotal * (length(y)-1)/(length(y)-length(p)) rsq_adj = 0.8945
在许多多项式回归模型中,对方程添加项会使 R2 和调整 R2 都增加。在前面的示例中,与线性拟合相比,使用三次拟合使这两种统计量都有所增加。(您可自行计算线性拟合的调整 R2,能够看到它具有较小的值。)但是,线性拟合并非始终差于更高阶拟合:更复杂拟合的调整 R2 也有可能低于更简单的拟合,此时表明增加复杂度并不适当。此外,虽然基本拟合工具生成的多项式回归模型的 R2 值始终在 0 和 1 之间变动,但某些模型的调整 R2 可能为负值,这表明该模型的项太多。
相关并不意味着因果性。因此,应始终谨慎解释相关性和确定系数。这些系数仅用来量化拟合模型对因变量方差的消除率。此类测度并不说明您的模型(或您选择的自变量)有多适合用于解释模型预测的变量行为。
用 Curve Fitting Toolbox 函数拟合数据
Curve Fitting Toolbox 通过启用以下数据拟合功能扩展 MATLAB 核心功能:
线性及非线性参数拟合,包括标准线性最小二乘、非线性最小二乘、加权最小二乘、约束最小二乘以及稳健拟合程序
非参数化拟合
确定拟合优度的统计量
外插、微分和积分
有助于数据分段及平滑处理的对话框
以不同的格式保存拟合结果,包括 MATLAB 代码文件、MAT 文件及工作区变量。
有关详细信息,请参阅Curve Fitting Toolbox。