使用拉普拉斯矩阵为图分区
此示例说明如何使用图的拉普拉斯矩阵来计算费德勒向量。费德勒向量可用于将图分区为两个子图。
加载数据
加载数据集 barbellgraph.mat,其中包含一个杠铃图的稀疏邻接矩阵和节点坐标。
load barbellgraph.mat绘制图
使用自定义节点坐标 xy 绘制图。
G = graph(A,'omitselfloops'); p = plot(G,'XData',xy(:,1),'YData',xy(:,2),'Marker','.'); axis equal
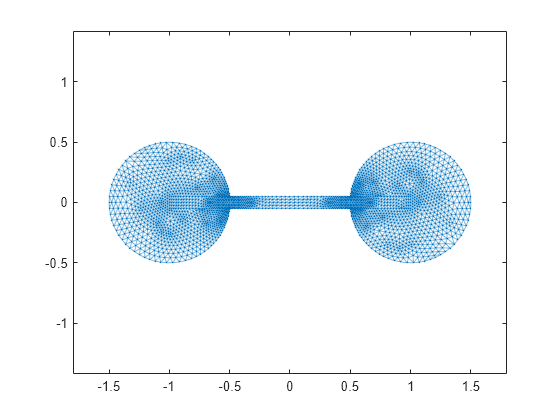
计算拉普拉斯矩阵和费德勒向量
计算图的拉普拉斯矩阵。然后,使用 eigs 计算两个模最小的特征值和相应的特征向量。
L = laplacian(G);
[V,D] = eigs(L,2,'smallestabs');费德勒向量是对应于该图的次最小特征值的特征向量。最小特征值为零,表示该图包含一个连通分量。这种情况下,V 中的第二列对应于次最小特征值 D(2,2)。
D
D = 2×2
10-3 ×
0.0000 0
0 0.2873
w = V(:,2);
由于仅计算特征值和特征向量的子集,因此使用 eigs 求费德勒向量的方法可扩展至更大的图,但对于较小的图而言,将拉普拉斯矩阵转换为满存储并使用 eig(full(L)) 同样切实可行。
为图分区
使用费德勒向量 w 将图分区为两个子图。如果一个节点在 w 中具有正值,则该节点将分配至子图 A。否则,该节点将分配至子图 B。这种做法称为符号切割或零阈值切割。符号切割最大限度减小了切割权重,该权重受限于图的任意非平凡切割的权重上界和下界。
使用符号切割对图进行分区。将 w>=0 的节点的子图突出显示为红色,将 w<0 的节点的子图突出显示为黑色。
highlight(p,find(w>=0),'NodeColor','r') % subgraph A highlight(p,find(w<0),'NodeColor','k') % subgraph B
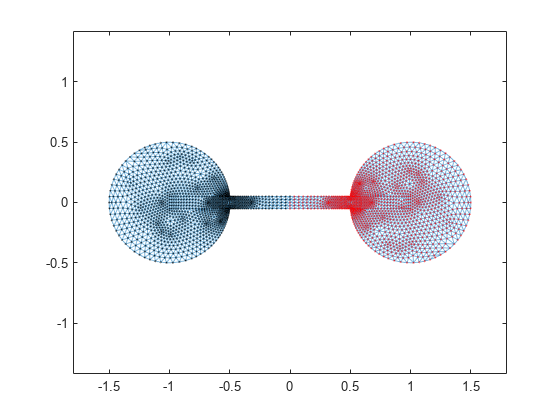
对于该杠铃图而言,此分区恰好将图平分为两个相等的节点集。但符号切割不总是生成平衡切割。
任何时候均可通过计算 w 的中位数并将其用作阈值来平分图。这种分区方法被称为中位数切割,它能保证每个子图具有相等的节点数量。
使用中位切割时,首先按中位数平移 w 中的值:
w_med = w - median(w);
然后,按 w_med 中的符号对图进行分区。对杠铃图而言,w 的中位数接近于零,因此两次切割会生成相似的平分。
另请参阅
graph | digraph | laplacian | subgraph