Solve System of PDEs with Initial Condition Step Functions

Open Live Script

This example shows how to solve a system of partial differential equations that uses step functions in the initial conditions.

Consider the PDEs

$\begin{array}{l} \frac{\partial n}{\partial t} = \frac{\partial}{\partial x} [d \frac{\partial n}{\partial x} - a n \frac{\partial c}{\partial x}] + S r n (N - n), \\ \frac{\partial c}{\partial t} = \frac{\partial^{2} c}{\partial x^{2}} + S (\frac{n}{n + 1} - c) . \end{array}$

The equations involve the constant parameters $d$ , $a$ , $S$ , $r$ , and $N$ , and are defined for $0 \leq x \leq 1$ and $t \geq 0$ . These equations arise in a mathematical model of the first steps of tumor-related angiogenesis [1]. $n (x, t)$ represents the cell density of endothelial cells, and $c (x, t)$ the concentration of a protein they release in response to the tumor.

This problem has a constant, steady state when

$[\begin{matrix} n_{0} \\ c_{0} \end{matrix}] = [\begin{matrix} 1 \\ 0.5 \end{matrix}]$ .

However, a stability analysis predicts evolution of the system to an inhomogeneous solution [1]. So step functions are used as the initial conditions to perturb the steady state and stimulate evolution of the system.

The boundary conditions require that both solution components have zero flux at $x = 0$ and $x = 1$ .

$\begin{array}{l} \frac{\partial}{\partial x} n (0, t) = \frac{\partial}{\partial x} n (1, t) = 0, \\ \frac{\partial}{\partial x} c (0, t) = \frac{\partial}{\partial x} c (1, t) = 0 . \end{array}$

To solve this system of equations in MATLAB®, you need to code the equations, initial conditions, and boundary conditions, then select a suitable solution mesh before calling the solver pdepe. You either can include the required functions as local functions at the end of a file (as done here), or save them as separate, named files in a directory on the MATLAB path.

Code Equation

Before you can code the equation, you need to make sure that it is in the form that the pdepe solver expects:

$c (x, t, u, \frac{\partial u}{\partial x}) \frac{\partial u}{\partial t} = x^{- m} \frac{\partial}{\partial x} (x^{m} f (x, t, u, \frac{\partial u}{\partial x})) + s (x, t, u, \frac{\partial u}{\partial x}) .$

Since there are two equations in the system of PDEs, the system of PDEs can be rewritten as

$[\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] \frac{\partial}{\partial t} [\begin{matrix} n \\ c \end{matrix}] = \frac{\partial}{\partial x} [\begin{matrix} d \frac{\partial n}{\partial x} - a n \frac{\partial c}{\partial x} \\ \frac{\partial c}{\partial x} \end{matrix}] + [\begin{matrix} S r n (N - n) \\ S (\frac{n}{n + 1} - c) \end{matrix}] .$

The values of the coefficients in the equation are then

$m = 0$

$c (x, t, u, \frac{\partial u}{\partial x}) = [\begin{matrix} 1 \\ 1 \end{matrix}]$ (diagonal values only)

$f (x, t, u, \frac{\partial u}{\partial x}) = [\begin{matrix} d \frac{\partial n}{\partial x} - a n \frac{\partial c}{\partial x} \\ \frac{\partial c}{\partial x} \end{matrix}]$

$s (x, t, u, \frac{\partial u}{\partial x}) = [\begin{matrix} S r n (N - n) \\ S (\frac{n}{n + 1} - c) \end{matrix}]$

Now you can create a function to code the equation. The function should have the signature [c,f,s] = angiopde(x,t,u,dudx):

x is the independent spatial variable.
t is the independent time variable.
u is the dependent variable being differentiated with respect to x and t. It is a two-element vector where u(1) is $n (x, t)$ and u(2) is $c (x, t)$ .
dudx is the partial spatial derivative $\partial u / \partial x$ . It is a two-element vector where dudx(1) is $\partial n / \partial x$ and dudx(2) is $\partial c / \partial x$ .
The outputs c, f, and s correspond to coefficients in the standard PDE equation form expected by pdepe.

As a result, the equations in this example can be represented by the function:

function [c,f,s] = angiopde(x,t,u,dudx)
d = 1e-3;
a = 3.8;
S = 3;
r = 0.88;
N = 1;

c = [1; 1];
f = [d*dudx(1) - a*u(1)*dudx(2)
     dudx(2)];
s = [S*r*u(1)*(N - u(1));
     S*(u(1)/(u(1) + 1) - u(2))];
end

(Note: All functions are included as local functions at the end of the example.)

Code Initial Conditions

Next, write a function that returns the initial condition. The initial condition is applied at the first time value and provides the value of $n (x, t_{0})$ and $c (x, t_{0})$ for any value of x. Use the function signature u0 = angioic(x) to write the function.

This problem has a constant, steady state when

$[\begin{matrix} n_{0} \\ c_{0} \end{matrix}] = [\begin{matrix} 1 \\ 0.5 \end{matrix}]$ .

However, a stability analysis predicts evolution of the system to an inhomogenous solution [1]. So, step functions are used as the initial conditions to perturb the steady state and stimulate evolution of the system.

$\begin{array}{l} u (x, 0) = [\begin{matrix} n_{0} \\ c_{0} \end{matrix}], \\ u (x, 0) = {\begin{matrix} 1.05 u_{1} & 0.3 \leq x \leq 0.6 \\ 1.0005 u_{2} & 0.3 \leq x \leq 0.6 \end{matrix} \end{array}$

The corresponding function is

function u0 = angioic(x)
u0 = [1; 0.5];
if x >= 0.3 && x <= 0.6
  u0(1) = 1.05 * u0(1);
  u0(2) = 1.0005 * u0(2);
end
end

Code Boundary Conditions

Now, write a function that evaluates the boundary conditions

$\begin{array}{l} \frac{\partial}{\partial x} n (0, t) = \frac{\partial}{\partial x} n (1, t) = 0, \\ \frac{\partial}{\partial x} c (0, t) = \frac{\partial}{\partial x} c (1, t) = 0 . \end{array}$

For problems posed on the interval $a \leq x \leq b$ , the boundary conditions apply for all $t$ and either $x = a$ or $x = b$ . The standard form for the boundary conditions expected by the solver is

$p (x, t, u) + q (x, t) f (x, t, u, \frac{\partial u}{\partial x}) = 0 .$

For $x = 0$ , the boundary condition equation is

$[\begin{array}{c} 0 \\ 0 \end{array}] + [\begin{array}{c} 1 \\ 1 \end{array}] \cdot [\begin{array}{c} d \frac{\partial n}{\partial x} - a n \frac{\partial c}{\partial x} \\ \frac{\partial c}{\partial x} \end{array}] = 0 .$

So the coefficients are:

$p_{L} (x, t, u) = [\begin{matrix} 0 \\ 0 \end{matrix}],$
$q_{L} (x, t) = [\begin{matrix} 1 \\ 1 \end{matrix}]$ .

For $x = 1$ the boundary conditions are the same, so $p_{R} (x, t, u) = [\begin{matrix} 0 \\ 0 \end{matrix}]$ and $q_{R} (x, t) = [\begin{matrix} 1 \\ 1 \end{matrix}]$ .

The boundary function should use the function signature [pl,ql,pr,qr] = angiobc(xl,ul,xr,ur,t), where:

The inputs xl and ul correspond to $u$ and $x$ for the left boundary.
The inputs xr and ur correspond to $u$ and $x$ for the right boundary.
t is the independent time variable.
The outputs pl and ql correspond to $p_{L} (x, t, u)$ and $q_{L} (x, t)$ for the left boundary ( $x = 0$ for this problem).
The outputs pr and qr correspond to $p_{R} (x, t, u)$ and $q_{R} (x, t)$ for the right boundary ( $x = 1$ for this problem).

The boundary conditions in this example are represented by the function:

function [pl,ql,pr,qr] = angiobc(xl,ul,xr,ur,t)
pl = [0; 0];
ql = [1; 1];
pr = pl;
qr = ql;
end

Select Solution Mesh

A long time interval is required to see the limiting behavior of the equations, so use 10 points in the interval $0 \leq t \leq 200$ . Also, the limit distribution of $c (x, t)$ varies by only about 0.1% over the interval $0 \leq x \leq 1$ , so a relatively fine spatial mesh with 50 points is appropriate.

x = linspace(0,1,50);
t = linspace(0,200,10);

Solve Equation

Finally, solve the equation using the symmetry $m$ , the PDE equation, the initial condition, the boundary conditions, and the meshes for $x$ and $t$ .

m = 0;
sol = pdepe(m,@angiopde,@angioic,@angiobc,x,t);

pdepe returns the solution in a 3-D array sol, where sol(i,j,k) approximates the kth component of the solution $u_{k}$ evaluated at t(i) and x(j). Extract the solution components into separate variables.

n = sol(:,:,1);
c = sol(:,:,2);

Plot Solution

Create a surface plot of the solution components $n$ and $c$ plotted at the selected mesh points for $x$ and $t$ .

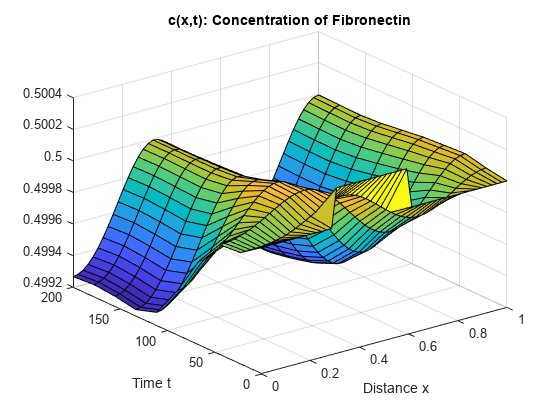
surf(x,t,c)
title('c(x,t): Concentration of Fibronectin')
xlabel('Distance x')
ylabel('Time t')

Figure contains an axes object. The axes object with title c(x,t): Concentration of Fibronectin, xlabel Distance x, ylabel Time t contains an object of type surface.

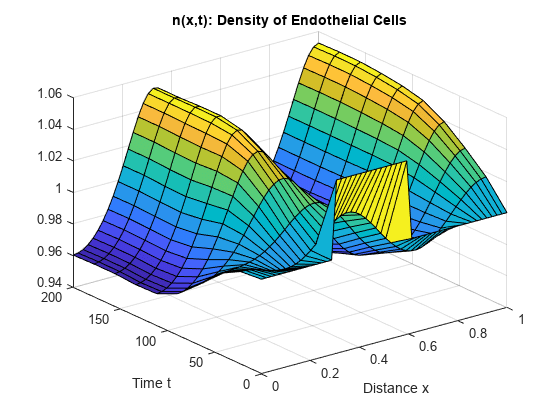
surf(x,t,n)
title('n(x,t): Density of Endothelial Cells')
xlabel('Distance x')
ylabel('Time t')

Figure contains an axes object. The axes object with title n(x,t): Density of Endothelial Cells, xlabel Distance x, ylabel Time t contains an object of type surface.

Now plot just the final distributions of the solutions at $t_{f} = 200$ . These plots correspond to Figures 3 and 4 in [1].

plot(x,n(end,:))
title('Final distribution of n(x,t_f)')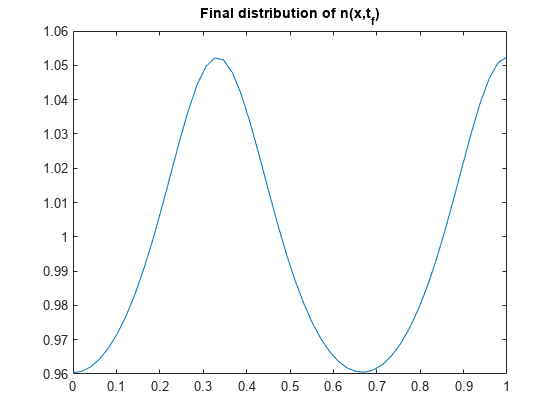

Figure contains an axes object. The axes object with title Final distribution of n(x,t indexOf f baseline ) contains an object of type line.

plot(x,c(end,:))
title('Final distribution of c(x,t_f)')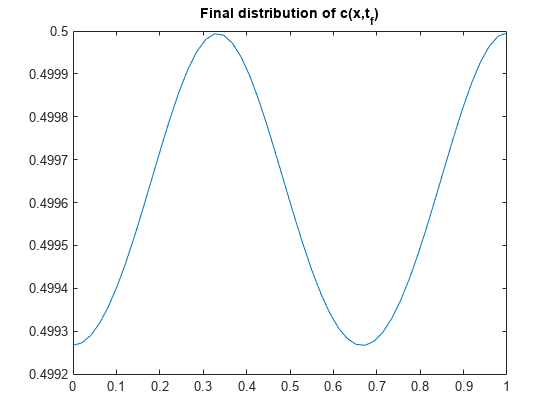

Figure contains an axes object. The axes object with title Final distribution of c(x,t indexOf f baseline ) contains an object of type line.

References

[1] Humphreys, M.E. and M.A.J. Chaplain. "A mathematical model of the first steps of tumour-related angiogenesis: Capillary sprout formation and secondary branching." IMA Journal of Mathematics Applied in Medicine & Biology, 13 (1996), pp. 73-98.

Local Functions

Listed here are the local helper functions that the PDE solver pdepe calls to calculate the solution. Alternatively, you can save these functions as their own files in a directory on the MATLAB path.

function [c,f,s] = angiopde(x,t,u,dudx) % Equation to solve
d = 1e-3;
a = 3.8;
S = 3;
r = 0.88;
N = 1;

c = [1; 1];
f = [d*dudx(1) - a*u(1)*dudx(2)
     dudx(2)];
s = [S*r*u(1)*(N - u(1));
     S*(u(1)/(u(1) + 1) - u(2))];
end
% ---------------------------------------------
function u0 = angioic(x) % Initial Conditions
u0 = [1; 0.5];
if x >= 0.3 && x <= 0.6
  u0(1) = 1.05 * u0(1);
  u0(2) = 1.0005 * u0(2);
end
end
% ---------------------------------------------
function [pl,ql,pr,qr] = angiobc(xl,ul,xr,ur,t) % Boundary Conditions
pl = [0; 0];
ql = [1; 1];
pr = pl;
qr = ql;
end
% ---------------------------------------------