求解 PDE 方程组

打开实时脚本

此示例说明由两个偏微分方程构成的方程组的解的构成，以及如何对解进行计算和绘图。

以如下 PDE 方程组为例

$\frac{\partial u_{1}}{\partial t} = 0.024 \frac{\partial^{2} u_{1}}{\partial x^{2}} - F (u_{1} - u_{2}),$

$\frac{\partial u_{2}}{\partial t} = 0.170 \frac{\partial^{2} u_{2}}{\partial x^{2}} + F (u_{1} - u_{2}) .$

（函数 $F (y) = e^{5.73 y} - e^{- 11.46 y}$ 用作速记形式。）

该公式在区间 $0 \leq x \leq 1$ 上对于时间 $t \geq 0$ 成立。初始条件为

$u_{1} (x, 0) = 1,$

$u_{2} (x, 0) = 0 .$

边界条件为

$\begin{array}{l} \frac{\partial}{\partial x} u_{1} (0, t) = 0, \\ u_{2} (0, t) = 0, \\ \frac{\partial}{\partial x} u_{2} (1, t) = 0, \\ u_{1} (1, t) = 1 . \end{array}$

要在 MATLAB® 中求解该方程，您需要对方程、初始条件和边界条件编写代码，然后在调用求解器 pdepe 之前选择合适的解网格。您可以将所需的函数作为局部函数包含在文件末尾（如本处所示），或者将它们作为单独的命名文件保存在 MATLAB 路径上的目录中。

编写方程代码

在编写方程代码之前，您需要确保它的形式符合 pdepe 求解器的要求：

$c (x, t, u, \frac{\partial u}{\partial x}) \frac{\partial u}{\partial t} = x^{- m} \frac{\partial}{\partial x} (x^{m} f (x, t, u, \frac{\partial u}{\partial x})) + s (x, t, u, \frac{\partial u}{\partial x}) .$

在此形式中，PDE 系数是矩阵值，方程变为

$[\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] \frac{\partial}{\partial t} [\begin{matrix} u_{1} \\ u_{2} \end{matrix}] = \frac{\partial}{\partial x} [\begin{matrix} 0.024 \frac{\partial u_{1}}{\partial x} \\ 0.170 \frac{\partial u_{2}}{\partial x} \end{matrix}] + [\begin{matrix} - F (u_{1} - u_{2}) \\ F (u_{1} - u_{2}) \end{matrix}] .$

因此，方程中的系数的值是

$m = 0$

$c (x, t, u, \frac{\partial u}{\partial x}) = [\begin{matrix} 1 \\ 1 \end{matrix}]$ （仅对角线值）

$f (x, t, u, \frac{\partial u}{\partial x}) = [\begin{matrix} 0.024 \frac{\partial u_{1}}{\partial x} \\ 0.170 \frac{\partial u_{2}}{\partial x} \end{matrix}]$

$s (x, t, u, \frac{\partial u}{\partial x}) = [\begin{matrix} - F (u_{1} - u_{2}) \\ F (u_{1} - u_{2}) \end{matrix}]$

现在，您可以创建一个函数以编写方程代码。该函数应具有签名 [c,f,s] = pdefun(x,t,u,dudx)：

x 是独立的空间变量。
t 是独立的时间变量。
u 是关于 x 和 t 微分的因变量。它是二元素向量，其中 u(1) 是 $u_{1} (x, t)$ ，u(2) 是 $u_{2} (x, t)$ 。
dudx 是偏空间导数 $\partial u / \partial x$ 。它是二元素向量，其中 dudx(1) 是 $\partial u_{1} / \partial x$ ，dudx(2) 是 $\partial u_{2} / \partial x$ 。
输出 c、f 和 s 对应于 pdepe 所需的标准 PDE 形式中的系数。

因此，此示例中的方程可由以下函数表示：

function [c,f,s] = pdefun(x,t,u,dudx)
c = [1; 1];
f = [0.024; 0.17] .* dudx;
y = u(1) - u(2);
F = exp(5.73*y)-exp(-11.47*y);
s = [-F; F];
end

（注意：所有函数都作为局部函数包含在示例的末尾。）

编写初始条件代码

接下来，编写一个返回初始条件的函数。初始条件应用在第一个时间值处，并为 x 的任何值提供 $u (x, t_{0})$ 的值。初始条件的数量必须等于方程的数量，因此对于此问题，有两个初始条件。使用函数签名 u0 = pdeic(x) 编写函数。

初始条件为

$u_{1} (x, 0) = 1,$

$u_{2} (x, 0) = 0 .$

对应的函数是

function u0 = pdeic(x)
u0 = [1; 0];
end

编写边界条件代码

现在，编写计算以下边界条件的函数

$\begin{array}{l} \frac{\partial}{\partial x} u_{1} (0, t) = 0, \\ u_{2} (0, t) = 0, \\ \frac{\partial}{\partial x} u_{2} (1, t) = 0, \\ u_{1} (1, t) = 1 . \end{array}$

对于在区间 $a \leq x \leq b$ 上提出的问题，边界条件应用于所有 $t$ 以及 $x = a$ 或 $x = b$ 。求解器所需的边界条件的标准形式是

$p (x, t, u) + q (x, t) f (x, t, u, \frac{\partial u}{\partial x}) = 0 .$

以这种形式编写， $u$ 的偏导数的边界条件需要用通量 $f (x, t, u, \frac{\partial u}{\partial x})$ 来表示。因此，此问题的边界条件是

对于 $x = 0$ ，方程为

$[\begin{matrix} 0 \\ u_{2} \end{matrix}] + [\begin{matrix} 1 \\ 0 \end{matrix}] \cdot [\begin{matrix} 0.024 \frac{\partial u_{1}}{\partial x} \\ 0.170 \frac{\partial u_{2}}{\partial x} \end{matrix}] = 0 .$

系数是：

$p_{L} (x, t, u) = [\begin{matrix} 0 \\ u_{2} \end{matrix}],$

$q_{L} (x, t) = [\begin{matrix} 1 \\ 0 \end{matrix}] .$

同样，对于 $x = 1$ ，方程是

$[\begin{matrix} u_{1} - 1 \\ 0 \end{matrix}] + [\begin{matrix} 0 \\ 1 \end{matrix}] \cdot [\begin{matrix} 0.024 \frac{\partial u_{1}}{\partial x} \\ 0.170 \frac{\partial u_{2}}{\partial x} \end{matrix}] = 0 .$

系数是：

$p_{R} (x, t, u) = [\begin{matrix} u_{1} - 1 \\ 0 \end{matrix}],$

$q_{R} (x, t) = [\begin{matrix} 0 \\ 1 \end{matrix}] .$

边界函数应使用函数签名 [pl,ql,pr,qr] = pdebc(xl,ul,xr,ur,t)：

对于左边界，输入 xl 和 ul 对应于 $u$ 和 $x$ 。
对于右边界，输入 xr 和 ur 对应于 $u$ 和 $x$ 。
t 是独立的时间变量。
对于左边界，输出 pl 和 ql 对应于 $p_{L} (x, t, u)$ 和 $q_{L} (x, t)$ （对于此问题， $x = 0$ ）。
对于右边界，输出 pr 和 qr 对应于 $p_{R} (x, t, u)$ 和 $q_{R} (x, t)$ （对于此问题， $x = 1$ ）。

此示例中的边界条件由以下函数表示：

function [pl,ql,pr,qr] = pdebc(xl,ul,xr,ur,t)
pl = [0; ul(2)];
ql = [1; 0];
pr = [ur(1)-1; 0];
qr = [0; 1];
end

选择解网格

当 $t$ 较小时，此问题的解会快速变化。虽然 pdepe 选择了适合解析急剧变化的时间步，但要在输出绘图中显示该行为，您需要选择适当的输出时间。对于空间网格，在 $0 \leq x \leq 1$ 两端的解中都存在边界层，因此您需要在那里指定网格点来解析急剧变化。

x = [0 0.005 0.01 0.05 0.1 0.2 0.5 0.7 0.9 0.95 0.99 0.995 1];
t = [0 0.005 0.01 0.05 0.1 0.5 1 1.5 2];

求解方程

最后，使用对称性值 $m$ 、PDE 方程、初始条件、边界条件以及 $x$ 和 $t$ 的网格来求解方程。

m = 0;
sol = pdepe(m,@pdefun,@pdeic,@pdebc,x,t);

pdepe 以三维数组 sol 形式返回解，其中 sol(i,j,k) 是在 t(i) 和 x(j) 处计算的解 $u_{k}$ 的第 k 个分量的逼近值。将每个解分量提取到一个单独变量中。

u1 = sol(:,:,1);
u2 = sol(:,:,2);

对解进行绘图

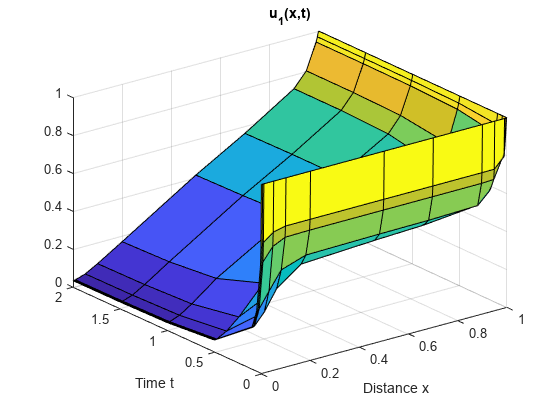
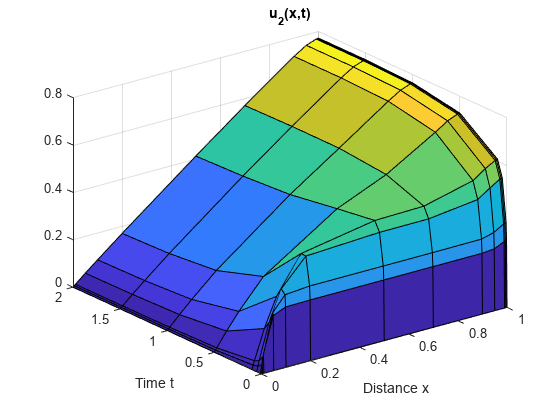
创建在 $x$ 和 $t$ 的所选网格点上绘制的 $u_{1}$ 和 $u_{2}$ 的解的曲面图。

surf(x,t,u1)
title('u_1(x,t)')
xlabel('Distance x')
ylabel('Time t')

Figure contains an axes object. The axes object with title u indexOf 1 baseline (x,t), xlabel Distance x, ylabel Time t contains an object of type surface.

surf(x,t,u2)
title('u_2(x,t)')
xlabel('Distance x')
ylabel('Time t')

Figure contains an axes object. The axes object with title u indexOf 2 baseline (x,t), xlabel Distance x, ylabel Time t contains an object of type surface.

局部函数

此处列出 PDE 求解器 pdepe 为计算解而调用的局部辅助函数。您也可以将这些函数作为它们自己的文件保存在 MATLAB 路径上的目录中。

function [c,f,s] = pdefun(x,t,u,dudx) % Equation to solve
c = [1; 1];
f = [0.024; 0.17] .* dudx;
y = u(1) - u(2);
F = exp(5.73*y)-exp(-11.47*y);
s = [-F; F];
end
% ---------------------------------------------
function u0 = pdeic(x) % Initial Conditions
u0 = [1; 0];
end
% ---------------------------------------------
function [pl,ql,pr,qr] = pdebc(xl,ul,xr,ur,t) % Boundary Conditions
pl = [0; ul(2)];
ql = [1; 0];
pr = [ur(1)-1; 0];
qr = [0; 1];
end
% ---------------------------------------------

另请参阅

pdepe