求解抛向空中的短棒的运动方程

打开实时脚本

此示例求解常微分方程组，该方程组对抛向空中的短棒的动态进行建模 [1]。短棒建模为两个质点 $m_{1}$ 和 $m_{2}$ 由长度为 $L$ 的棒连接。短棒抛向空中，随后在重力作用下在垂直 xy 平面内移动。棒与水平线构成角度 $θ$ ，第一个质点的坐标是 $(x, y)$ 。根据此公式，第二个质点的坐标是 $(x + L \cos θ, y + L \sin θ)$ 。

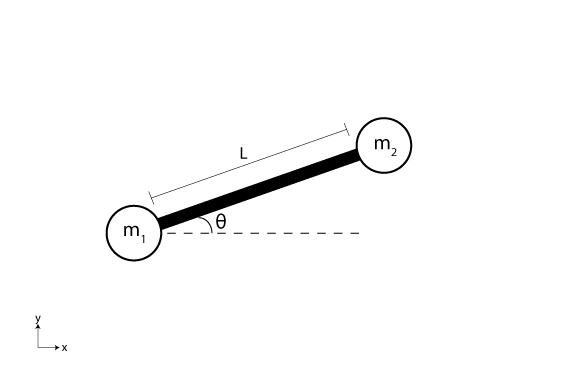
系统的运动方程是通过对三个坐标 $x$ 、 $y$ 和 $θ$ 中的每个坐标应用拉格朗日方程获得的：

$\begin{array}{l} (m_{1} + m_{2}) \ddot{x} - m_{2} L \ddot{θ} \sin θ - m_{2} L {\dot{θ}}^{2} \cos θ = 0, \\ (m_{1} + m_{2}) \ddot{y} - m_{2} L \ddot{θ} \cos θ - m_{2} L {\dot{θ}}^{2} \sin θ + (m_{1} + m_{2}) g = 0, \\ L^{2} \ddot{θ} - L \ddot{x} \sin θ + L \ddot{y} \cos θ + g L \cos θ = 0 . \end{array}$

编写方程代码

MATLAB 要求将方程写作 $\dot{q} = f (t, q)$ 形式，其中 $\dot{q}$ 是每个坐标的一阶导数。在此问题中，解向量有六个分量： $x$ 、 $y$ 、角度 $θ$ 及各自的一阶导数：

$q = [\begin{array}{c} q_{1} \\ q_{2} \\ q_{3} \\ q_{4} \\ q_{5} \\ q_{6} \end{array}] = [\begin{array}{c} x \\ \dot{x} \\ y \\ \dot{y} \\ θ \\ \dot{θ} \end{array}] .$

通过此表示法，您可以用 $q$ 的元素彻底重写运动方程：

$\begin{array}{l} (m_{1} + m_{2}) \dot{q_{2}} - m_{2} L \dot{q_{6}} \sin q_{5} = m_{2} L q_{6}^{2} \cos q_{5}, \\ (m_{1} + m_{2}) \dot{q_{4}} - m_{2} L \dot{q_{6}} \cos q_{5} = m_{2} L q_{6}^{2} \sin q_{5} - (m_{1} + m_{2}) g, \\ L^{2} \dot{q_{6}} - L \dot{q_{2}} \sin q_{5} + L \dot{q_{4}} \cos q_{5} = - g L \cos q_{5} . \end{array}$

遗憾的是，运动方程不符合求解器要求的形式 $\dot{q} = f (t, q)$ ，因为左侧有几个具有一阶导数的项。出现这种情况时，必须使用质量矩阵来表示方程的左侧。

通过矩阵表示法，您可以使用 $M (t, q) \dot{q} = f (t, q)$ 形式的质量矩阵将运动方程重写为包含六个方程的方程组。质量矩阵用矩阵-向量积表示方程左侧的一阶导数的线性组合。在此形式中，方程组变为：

$[\begin{array}{c} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & m_{1} + m_{2} & 0 & 0 & 0 & - m_{2} L \sin q_{5} \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & m_{1} + m_{2} & 0 & m_{2} L \cos q_{5} \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & - L \sin q_{5} & 0 & L \cos q_{5} & 0 & L^{2} \end{array}] [\begin{array}{c} \dot{q_{1}} \\ \dot{q_{2}} \\ \dot{q_{3}} \\ \dot{q_{4}} \\ \dot{q_{5}} \\ \dot{q_{6}} \end{array}] = [\begin{array}{c} q_{2} \\ m_{2} L q_{6}^{2} \cos q_{5} \\ q_{4} \\ m_{2} L q_{6}^{2} \sin q_{5} - (m_{1} + m_{2}) g \\ q_{6} \\ - g L \cos q_{5} \end{array}]$

根据此表达式，您可以编写一个用于计算质量矩阵的非零元素的函数。该函数接受三个输入： $t$ 和解向量 $q$ （这两个输入是必需的，即使这些输入在函数体中不使用，您也必须指定这些输入），以及 $P$ （可选的额外输入，用于传入参数值）。

function M = mass(t,q,P)
% Extract parameters
m1 = P(1);
m2 = P(2);
L = P(3);
g = P(4);

% Mass matrix elements
M = zeros(6,6);
M(1,1) = 1;
M(2,2) = m1 + m2;
M(2,6) = -m2*L*sin(q(5));
M(3,3) = 1;
M(4,4) = m1 + m2;
M(4,6) = m2*L*cos(q(5));
M(5,5) = 1;
M(6,2) = -L*sin(q(5));
M(6,4) = L*cos(q(5));
M(6,6) = L^2;
end

接下来，您可以为方程组 $M (t, q) \dot{q} = f (t, q)$ 中的每个方程的右侧编写一个函数。与质量矩阵函数一样，此函数接受两个必需的输入 $t$ 和 $q$ ，以及一个用于参数值的可选输入 $P$ 。

function dydt = f(t,q,P)
% Extract parameters
m1 = P(1);
m2 = P(2);
L = P(3);
g = P(4);

% Equations to solve
dydt = [q(2)
        m2*L*q(6)^2*cos(q(5))
        q(4)
        m2*L*q(6)^2*sin(q(5))-(m1+m2)*g
        q(6)
        -g*L*cos(q(5))];
end

求解方程组

首先，为 $m_{1}$ 、 $m_{2}$ 、 $L$ 和 $g$ 创建一个由参数值组成的向量 P。求解器将向量 P 作为额外输入传递给质量矩阵和 ODE 函数。

P = [0.1 0.1 1 9.81];

为问题创建一个初始条件向量。由于短棒以一定角度向上投掷，因此初始速度应使用非零值，即 $\dot{x_{0}} = 4$ 、 $\dot{y_{0}} = 20$ 和 $\dot{θ_{0}} = 2$ 。短棒的初始位置从直立位置开始，即 $θ_{0} = - π / 2$ 、 $x_{0} = 0$ 和 $y_{0} = L$ 。

y0 = [0; 4; P(3); 20; -pi/2; 2];

现在，创建一个 ode 对象来表示问题，为 ODEFcn、MassMatrix、InitialValue 和 Parameters 指定值。对象显示表明，因为存在质量矩阵，已为该问题选择 ode15s 求解器。

F = ode(ODEFcn=@f,...
        MassMatrix=@mass,...
        InitialValue=y0,...
        Parameters=P)

F = 
  ode with properties:

   Problem definition
               ODEFcn: @f
           Parameters: [0.1000 0.1000 1 9.8100]
          InitialTime: 0
         InitialValue: [6x1 double]
             Jacobian: []
           MassMatrix: [1x1 odeMassMatrix]
         EquationType: standard

   Solver properties
    AbsoluteTolerance: 1.0000e-06
    RelativeTolerance: 1.0000e-03
               Solver: auto
       SelectedSolver: ode15s

  Show all properties

为积分时间跨度创建一个由 0 和 4 之间的 25 个点组成的向量，并使用 solve 仿真方程组。当您指定时间向量时，求解器会采用它自己的内部步长，但在您指定的点对解进行插值。

tspan = linspace(0,4,25);
sol = solve(F,tspan)

sol = 
  ODEResults with properties:

        Time: [0 0.1667 0.3333 0.5000 0.6667 0.8333 1 1.1667 1.3333 1.5000 1.6667 1.8333 2 2.1667 2.3333 2.5000 2.6667 2.8333 3 3.1667 3.3333 3.5000 3.6667 3.8333 4]
    Solution: [6x25 double]

绘制结果

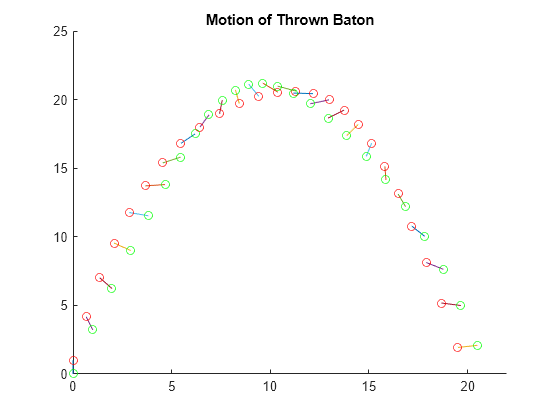
solve 的输出包含运动方程在每个请求的时间步的解。为了检验结果，对短棒随时间的运动轨迹绘图。

遍历解的每列，并在每个时间步绘制短棒的位置。给短棒的每端涂上不同颜色，以便看到它随时间的旋转。

figure
title("Motion of Thrown Baton");
axis([0 22 0 25])
hold on
for j = 1:length(sol.Time)
   theta = sol.Solution(5,j);
   X = sol.Solution(1,j);
   Y = sol.Solution(3,j);
   xvals = [X X+P(3)*cos(theta)];
   yvals = [Y Y+P(3)*sin(theta)];
   plot(xvals,yvals,xvals(1),yvals(1),"ro",xvals(2),yvals(2),"go")
end
hold off

Figure contains an axes object. The axes object with title Motion of Thrown Baton contains 75 objects of type line. One or more of the lines displays its values using only markers

参考

[1] Wells, Dare A. Schaum’s Outline of Theory and Problems of Lagrangian Dynamics:With a Treatment of Euler’s Equations of Motion, Hamilton’s Equations and Hamilton’s Principle.Schaum's Outline Series.New York:Schaum Pub.Co, 1967.

另请参阅

ode45

求解抛向空中的短棒的运动方程

编写方程代码

求解方程组

绘制结果

参考

另请参阅

相关主题

WeChat