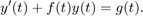ode45

求解非刚性微分方程 - 中阶方法

语法

[t,y] = ode45(odefun,tspan,y0)

[t,y] = ode45(odefun,tspan,y0,options)

[t,y,te,ye,ie] = ode45(odefun,tspan,y0,options)

sol = ode45(___)

说明

[t,y] = ode45(odefun,tspan,y0)（其中 tspan = [t0 tf]）求微分方程组 $y' = f (t, y)$ 从 t0 到 tf 的积分，初始条件为 y0。解数组 y 中的每一行都与列向量 t 中返回的值相对应。

所有 MATLAB^® ODE 求解器都可以解算 $y' = f (t, y)$ 形式的方程组，或涉及质量矩阵 $M (t, y) y' = f (t, y)$ 的问题。求解器都使用类似的语法。ode23s 求解器只能解算质量矩阵为常量的问题。ode15s 和 ode23t 可以解算具有奇异质量矩阵的问题，称为微分代数方程 (DAE)。使用 odeset 的 Mass 选项指定质量矩阵。

ode45 是一个通用型 ODE 求解器，是您解算大多数问题时的首选。但是，对于刚性问题或需要较高准确性的问题，其他 ODE 求解器可能更适合。有关详细信息，请参阅选择 ODE 求解器。

示例

[t,y] = ode45(odefun,tspan,y0,options) 还使用由 options（使用 odeset 函数创建的参量）定义的积分设置。例如，使用 AbsTol 和 RelTol 选项指定绝对误差容限和相对误差容限，或者使用 Mass 选项提供质量矩阵。

示例

[t,y,te,ye,ie] = ode45(odefun,tspan,y0,options) 还求 (t,y) 的函数（称为事件函数）在何处为零。在输出中，te 是事件的时间，ye 是事件发生时的解，ie 是触发的事件的索引。

对于每个事件函数，应指定积分是否在零点处终止以及过零方向是否重要。为此，请将 'Events' 属性设置为函数（例如 myEventFcn 或 @myEventFcn），并创建一个对应的函数：[value,isterminal,direction] = myEventFcn(t,y)。有关详细信息，请参阅 ODE 事件位置。

sol = ode45(___) 返回一个结构体，您可以将该结构体与 deval 结合使用来计算区间 [t0 tf] 中任意点位置的解。您可以使用上述语法中的任何输入参量组合。

示例

全部折叠

具有一个解分量的 ODE

打开实时脚本

在对求解器的调用中，可将只有一个解分量的简单 ODE 指定为匿名函数。该匿名函数必须同时接受两个输入 (t,y)，即使在该函数中一个输入未使用也是如此。

解算 ODE

$y^{'} = 2 t .$

指定时间区间 [0 5] 和初始条件 y0 = 0。

tspan = [0 5];
y0 = 0;
[t,y] = ode45(@(t,y) 2*t, tspan, y0);

对解绘图。

plot(t,y,'-o')

Figure contains an axes object. The axes object contains an object of type line.

解算非刚性方程

打开实时脚本

van der Pol 方程为二阶 ODE

$y_{1}^{''} - μ (1 - y_{1}^{2}) y_{1}^{'} + y_{1} = 0,$

其中 $μ > 0$ 为标量参数。通过执行 $y_{1}^{'} = y_{2}$ 代换，将此方程重写为一阶 ODE 方程组。生成的一阶 ODE 方程组为

$\begin{array}{cl} y_{1}^{'} & = y_{2} \\ y_{2}^{'} & = μ (1 - y_{1}^{2}) y_{2} - y_{1} . \end{array}$

函数文件 vdp1.m 代表使用 $μ = 1$ 的 van der Pol 方程。变量 $y_{1}$ 和 $y_{2}$ 是二元素向量 dydt 的项 y(1) 和 y(2)。

function dydt = vdp1(t,y)
%VDP1  Evaluate the van der Pol ODEs for mu = 1
%
%   See also ODE113, ODE23, ODE45.

%   Jacek Kierzenka and Lawrence F. Shampine
%   Copyright 1984-2014 The MathWorks, Inc.

dydt = [y(2); (1-y(1)^2)*y(2)-y(1)];

使用 ode45 函数、时间区间 [0 20] 和初始值 [2 0] 来解算该 ODE。生成的输出即为时间点 t 的列向量和解数组 y。y 中的每一行都与 t 的相应行中返回的时间相对应。y 的第一列与 $y_{1}$ 相对应，第二列与 $y_{2}$ 相对应。

[t,y] = ode45(@vdp1,[0 20],[2; 0]);

绘制 $y_{1}$ 和 $y_{2}$ 的解对 t 的图。

plot(t,y(:,1),'-o',t,y(:,2),'-o')
title('Solution of van der Pol Equation (\mu = 1) with ODE45');
xlabel('Time t');
ylabel('Solution y');
legend('y_1','y_2')

Figure contains an axes object. The axes object with title Solution of van der Pol Equation ( mu blank = blank 1 ) with ODE45, xlabel Time t, ylabel Solution y contains 2 objects of type line. These objects represent y_1, y_2.

向 ODE 函数传递额外的参数

打开实时脚本

ode45 仅适用于使用两个输入参量（t 和 y）的函数。但是，通过在函数外部定义参数并在指定函数句柄时传递这些参数，可以传入额外参数。

解算 ODE

$y^{''} = \frac{A}{B} t y .$

将该方程重写为一阶方程组可以得到

$\begin{array}{cl} y_{1}^{'} & = y_{2} \\ y_{2}^{'} & = \frac{A}{B} t y_{1} . \end{array}$

此示例末尾包含的局部函数 odefcn 将此方程组表示为接受四个输入参量（t、y、A 和 B）的函数。

function dydt = odefcn(t,y,A,B)
  dydt = zeros(2,1);
  dydt(1) = y(2);
  dydt(2) = (A/B)*t.*y(1);
end

使用 ode45 解算 ODE。指定函数句柄，使其将 A 和 B 的预定义值传递给 odefcn。

A = 1;
B = 2;
tspan = [0 5];
y0 = [0 0.01];
[t,y] = ode45(@(t,y) odefcn(t,y,A,B), tspan, y0);

绘制结果。

plot(t,y(:,1),'-o',t,y(:,2),'-.')

Figure contains an axes object. The axes object contains 2 objects of type line.

function dydt = odefcn(t,y,A,B)
  dydt = zeros(2,1);
  dydt(1) = y(2);
  dydt(2) = (A/B)*t.*y(1);
end

求解具有多个初始条件的 ODE

打开实时脚本

对于只有一个方程的简单 ODE 方程组，可以将 y0 指定为一个包含多个初始条件的向量。此方法通过标量扩展创建一个由独立方程组成的方程组，每个初始值对应一个方程，ode45 求解该方程组以针对每个初始值生成结果。

创建一个匿名函数来表示方程 $f (t, y) = - 2 y + 2 \cos (t) \sin (2 t)$ 。该函数必须接受分别对应于 t 和 y 的两个输入。

yprime = @(t,y) -2*y + 2*cos(t).*sin(2*t);

创建一个由范围 $[- 5, 5]$ 内的不同初始条件组成的向量。

y0 = -5:5;

使用 ode45 计算方程在时间区间 $[0, 3]$ 内针对每个初始条件的解。

tspan = [0 3];
[t,y] = ode45(yprime,tspan,y0);

绘制结果。

plot(t,y)
grid on
xlabel('t')
ylabel('y')
title('Solutions of y'' = -2y + 2 cos(t) sin(2t), y(0) = -5,-4,...,4,5','interpreter','latex')

Figure contains an axes object. The axes object with title Solutions of y' = -2y + 2 cos(t) sin(2t), y(0) = -5,-4,...,4,5, xlabel t, ylabel y contains 11 objects of type line.

此方法对于求解具有多个初始条件的简单 ODE 非常有用。然而，该方法也有一些折衷：

您无法求解具有多个初始条件的方程组。该方法仅适用于求解一个具有多个初始条件的方程。
求解器在每步选择的时间步基于方程组中需要采取最小步长的方程。这意味着求解器可以采取小步长来满足一个初始条件的方程，但其他方程如果单独求解的话将使用不同步长。尽管如此，同时针对多个初始条件进行求解通常比使用 for 循环分别求解方程更快。

有关此方法的详细信息，请参阅求解具有多个初始条件的 ODE 方程组。

带有时间依赖项的 ODE

打开脚本

请考虑以下带有时间依赖参数的 ODE：

$$y'(t) + f(t)y(t) = g(t).$$

初始条件为 $y_0 = 1$ 。函数 f(t) 由在时间 ft 时计算的 n×1 向量 f 定义。函数 g(t) 由在时间 gt 时计算的 m×1 向量 g 定义。

创建向量 f 和 g。

ft = linspace(0,5,25);
f = ft.^2 - ft - 3;

gt = linspace(1,6,25);
g = 3*sin(gt-0.25);

编写名为 myode 的函数，该函数通过对 f 和 g 进行插值获取时间依赖项在指定时间的值。将函数保存到您当前的文件夹中，以运行示例的其余部分。

myode 函数接受额外的输入参量以计算每个时间步的 ODE，但 ode45 只使用前两个输入参量 t 和 y。

function dydt = myode(t,y,ft,f,gt,g)
f = interp1(ft,f,t); % Interpolate the data set (ft,f) at time t
g = interp1(gt,g,t); % Interpolate the data set (gt,g) at time t
dydt = -f.*y + g; % Evaluate ODE at time t

使用 ode45 计算方程在时间区间 [1 5] 内的解。使用函数句柄指定函数，从而使 ode45 只使用 myode 的前两个输入参量。此外，使用 odeset 放宽误差阈值。

tspan = [1 5];
ic = 1;
opts = odeset('RelTol',1e-2,'AbsTol',1e-4);
[t,y] = ode45(@(t,y) myode(t,y,ft,f,gt,g), tspan, ic, opts);

绘制解 y 对时间点 t 的函数图。

plot(t,y)

计算和扩展解结构体

打开实时脚本

van der Pol 方程为二阶 ODE

$y_{1}^{''} - μ (1 - y_{1}^{2}) y_{1}^{'} + y_{1} = 0 .$

使用 ode45 以及 $μ = 1$ 解算 van der Pol 方程。函数 vdp1.m 随 MATLAB® 一起提供，用于对方程进行编码。指定单个输出以返回包含解信息（如求解器和计算点）的结构体。

tspan = [0 20];
y0 = [2 0];
sol = ode45(@vdp1,tspan,y0)

sol = struct with fields:
     solver: 'ode45'
    extdata: [1x1 struct]
          x: [0 1.0048e-04 6.0285e-04 0.0031 0.0157 0.0785 0.2844 0.5407 0.8788 1.4032 1.8905 2.3778 2.7795 3.1285 3.4093 3.6657 3.9275 4.2944 4.9013 5.3506 5.7998 6.2075 6.5387 6.7519 6.9652 7.2247 7.5719 8.1226 8.6122 9.1017 9.5054 ... ] (1x60 double)
          y: [2x60 double]
      stats: [1x1 struct]
      idata: [1x1 struct]

使用 linspace 在区间 [0 20] 内生成 250 个点。使用 deval 计算在这些点上的解。

x = linspace(0,20,250);
y = deval(sol,x);

绘制解的第一个分量。

plot(x,y(1,:))

Figure contains an axes object. The axes object contains an object of type line.

使用 odextend 将解扩展到 $t_{f} = 35$ ，并将结果添加到原始图中。

sol_new = odextend(sol,@vdp1,35);
x = linspace(20,35,350);
y = deval(sol_new,x);
hold on
plot(x,y(1,:),'r')

Figure contains an axes object. The axes object contains 2 objects of type line.

输入参数

全部折叠

`odefun` — 要求解的函数
函数句柄

要求解的函数，指定为指向待积分器的句柄。

对于标量 t 和列向量 y 来说，函数 dydt = odefun(t,y) 必须返回数据类型为 single 或 double 的列向量 dydt，该列向量对应于 $f (t, y)$ 。odefun 必须同时接受输入参量 t 和 y，即使其中一个参量未在函数中使用也是如此。

例如，要解算 $y' = 5 y - 3$ ，请使用此函数：

function dydt = odefun(t,y)
dydt = 5*y-3;
end

对于方程组，odefun 的输出为向量。向量中的每个元素均为一个方程右侧的计算值。例如，考虑以下包含两个方程的方程组

$\begin{array}{l} y'_{1} = y_{1} + 2 y_{2} \\ y'_{2} = 3 y_{1} + 2 y_{2} \end{array}$

计算每个时间步下每个方程右侧值的函数为

function dydt = odefun(t,y)
dydt = zeros(2,1);
dydt(1) = y(1)+2*y(2);
dydt(2) = 3*y(1)+2*y(2);
end

有关如何为函数 odefun 提供其他参数的信息，请参阅参数化函数。

示例: @myFcn

数据类型: function_handle

`tspan` — 积分区间
向量

积分区间，指定为向量。至少，tspan 必须是指定初始时间和最终时间的二元素向量 [t0 tf]。要获取 t0 到 tf 之间的特定时间的解，请使用 [t0,t1,t2,...,tf] 形式的长向量。tspan 中的元素必须单调递增或单调递减。

求解器在初始时间 tspan(1) 施加由 y0 给出的初始条件，然后求 tspan(1) 到 tspan(end) 的积分：

如果 tspan 有两个元素 [t0 tf]，求解器将返回在该区间内的每个内部积分步计算的解。
如果 tspan 包含两个以上的元素，[t0,t1,t2,...,tf]，求解器将返回在给定点处计算的解。但是，求解器不会精确步进到 tspan 中指定的每个点。此时，求解器使用自己的内部积分步来计算解，然后在 tspan 中请求的各点处计算解。在指定点处生成的解与在每个内部积分步计算的解具有相同的准确度级别。
指定多个中间点对计算效率影响甚微，但对于大型系统可能会影响内存管理。

求解器使用 tspan 的值计算 InitialStep 和 MaxStep 的合适值：

如果 tspan 包含多个中间点 [t0,t1,t2,...,tf]，则指定的点表示了问题的规模，这可能影响求解器使用的 InitialStep 的值。因此，根据您是将 tspan 指定为二元素向量还是包含中间点的向量，求解器获得的解可能有所不同。
tspan 中的初始值和最终值用于计算最大步长 MaxStep。因此，更改 tspan 中的初始值或最终值可能导致求解器使用不同步长序列，从而可能会更改解。

示例: [1 10]

示例: [1 3 5 7 9 10]

数据类型: single | double

`y0` — 初始条件
向量

初始条件，指定为向量。y0 的长度必须与 odefun 的向量输出相同，使 y0 为 odefun 中定义的每个方程包含一个初始条件。

数据类型: single | double

`options` — options 结构体
结构体数组

options 结构体，指定为结构体数组。使用 odeset 函数创建或修改 options 结构体。有关与每个求解器兼容的选项列表，请参阅 ODE 选项摘要。

示例: options = odeset('RelTol',1e-5,'Stats','on','OutputFcn',@odeplot) 指定 1e-5 的相对误差容限、打开求解器统计信息的显示，并指定输出函数 @odeplot 在计算时绘制解。

数据类型: struct

输出参量

全部折叠

`t` — 求值点
列向量

计算点，以列向量形式返回。

如果 tspan 包含两个元素 [t0 tf]，则 t 包含用于执行积分的内部计算点。
如果 tspan 包含两个以上元素，则 t 与 tspan 相同。

`y` — 解
数组

解，以数组形式返回。y 中的每一行都与 t 的相应行中返回的值处的解相对应。

`te` — 事件的时间
列向量

事件的时间，以列向量形式返回。te 中的事件时间对应于 ye 中返回的解，而 ie 指定发生了哪个事件。

`ye` — 事件时间处的解
数组

事件时间的解，以数组形式返回。te 中的事件时间对应于 ye 中返回的解，而 ie 指定发生了哪个事件。

`ie` — 触发的事件函数的索引
列向量

触发的事件函数的索引，以列向量形式返回。te 中的事件时间对应于 ye 中返回的解，而 ie 指定发生了哪个事件。

`sol` — 用于计算的结构体
结构体数组

用于计算的结构体，以结构体数组形式返回。此结构体与 deval 函数一起使用，用于计算区间 [t0 tf] 内任何点的解。sol 结构体数组始终包括下列字段：

结构体字段	描述
`sol.x`	求解器选择的步的行向量。
`sol.y`	解。每列 `sol.y(:,i)` 包含时间 `sol.x(i)` 处的解。
`sol.solver`	求解器名称。

此外，如果指定了 odeset 的 Events 选项并且检测到事件，则 sol 还包括下列字段：

结构体字段	描述
`sol.xe`	事件发生的点。`sol.xe(end)` 包含终止事件（如果有）的确切点。
`sol.ye`	与 `sol.xe` 中的事件相对应的解。
`sol.ie`	`Events` 选项中指定的函数所返回的向量的索引。这些值指示求解器检测到的事件。

算法

ode45 基于显式龙格-库塔 (4,5) 公式多曼-普林斯对。这是一种单步求解器 – 在计算 y(t_n) 时，该求解器仅需要最靠近该时间点的前一时间点处的解 y(t_n-1) [1], [2]。

参考

[1] Dormand, J. R. and P. J. Prince, “A family of embedded Runge-Kutta formulae,” J. Comp. Appl. Math., Vol. 6, 1980, pp. 19–26.

[2] Shampine, L. F. and M. W. Reichelt, “The MATLAB ODE Suite,” SIAM Journal on Scientific Computing, Vol. 18, 1997, pp. 1–22.

扩展功能

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

所有 odeset 选项参量都必须为常量。
代码生成不支持在 options 结构体中使用常量质量矩阵。需以函数形式提供质量矩阵。
必须提供至少两个输出参量 T 和 Y。
输入类型必须为同类 - 全部为双精度或全部为单精度。
必须启用可变大小支持。当 tspan 有两个元素或当您使用事件函数时，代码生成需要动态分配内存。

版本历史记录

在 R2006a 之前推出

另请参阅

ode23 | ode78 | ode89 | ode113 | ode15s | odeset | odeget | deval | odextend

ode45

语法

说明

示例

具有一个解分量的 ODE

解算非刚性方程

向 ODE 函数传递额外的参数

求解具有多个初始条件的 ODE

带有时间依赖项的 ODE

计算和扩展解结构体

输入参数

odefun — 要求解的函数 函数句柄

tspan — 积分区间 向量

y0 — 初始条件 向量

options — options 结构体 结构体数组

输出参量

t — 求值点 列向量

y — 解 数组

te — 事件的时间 列向量

ye — 事件时间处的解 数组

ie — 触发的事件函数的索引 列向量

sol — 用于计算的结构体 结构体数组

算法

参考

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

版本历史记录

另请参阅

主题

WeChat

`odefun` — 要求解的函数
函数句柄

`tspan` — 积分区间
向量

`y0` — 初始条件
向量

`options` — options 结构体
结构体数组

`t` — 求值点
列向量

`y` — 解
数组

`te` — 事件的时间
列向量

`ye` — 事件时间处的解
数组

`ie` — 触发的事件函数的索引
列向量

`sol` — 用于计算的结构体
结构体数组

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。