ode78

求解非刚性微分方程 - 高阶方法

自 R2021b 起

全页折叠

语法

[t,y] = ode78(odefun,tspan,y0)

[t,y] = ode78(odefun,tspan,y0,options)

[t,y,te,ye,ie] = ode78(odefun,tspan,y0,options)

sol = ode78(___)

说明

[t,y] = ode78(odefun,tspan,y0)（其中 tspan = [t0 tf]）求微分方程组 $y' = f (t, y)$ 从 t0 到 tf 的积分，初始条件为 y0。解数组 y 中的每一行都与列向量 t 中返回的值相对应。

所有 MATLAB^® ODE 求解器都可以解算 $y' = f (t, y)$ 形式的方程组，或涉及质量矩阵 $M (t, y) y' = f (t, y)$ 的问题。求解器使用类似的语法。ode23s 求解器只能解算质量矩阵为常量的问题。ode15s 和 ode23t 可以解算具有奇异质量矩阵的问题，称为微分代数方程 (DAE)。使用 odeset 的 Mass 选项指定质量矩阵。

示例

[t,y] = ode78(odefun,tspan,y0,options) 还使用由 options（使用 odeset 函数创建的参量）定义的积分设置。例如，设置 AbsTol 和 RelTol 选项指定绝对误差容限和相对误差容限，或者设置 Mass 选项提供质量矩阵。

[t,y,te,ye,ie] = ode78(odefun,tspan,y0,options) 还求 (t,y) 的函数（称为事件函数）在何处为零。在输出中，te 是事件的时间，ye 是事件发生时的解，ie 是触发的事件的索引。

对于每个事件函数，应指定积分是否在零点处终止以及过零方向是否重要。为此，请将 odeset 的 'Events' 选项设置为函数（例如 myEventFcn 或 @myEventFcn），并创建一个对应的函数：[value,isterminal,direction] = myEventFcn(,,t,y)。有关详细信息，请参阅 ODE 事件位置。

sol = ode78(___) 返回一个结构体，您可以将该结构体与 deval 结合使用来计算区间 [t0 tf] 中任意点位置的解。您可以使用上述语法中的任何输入参量组合。

示例

全部折叠

具有一个解分量的 ODE

打开实时脚本

在对求解器的调用中，可将只有一个解分量的简单 ODE 指定为匿名函数。该匿名函数必须同时接受两个输入 (t,y)，即使在该函数中一个输入未使用也是如此。

解算 ODE

$y^{'} = 2 t .$

指定时间区间 [0 5] 和初始条件 y0 = 0。

tspan = [0 5];
y0 = 0;
[t,y] = ode78(@(t,y) 2*t, tspan, y0);

对解绘图。

plot(t,y,'-o')

Figure contains an axes object. The axes object contains an object of type line.

解算非刚性方程

打开实时脚本

van der Pol 方程为二阶 ODE

$y_{1}^{''} - μ (1 - y_{1}^{2}) y_{1}^{'} + y_{1} = 0,$

其中 $μ > 0$ 为标量参数。通过执行 $y_{1}^{'} = y_{2}$ 代换，将此方程重写为一阶 ODE 方程组。生成的一阶 ODE 方程组为

$\begin{array}{cl} y_{1}^{'} & = y_{2} \\ y_{2}^{'} & = μ (1 - y_{1}^{2}) y_{2} - y_{1} . \end{array}$

函数文件 vdp1.m 代表使用 $μ = 1$ 的 van der Pol 方程。变量 $y_{1}$ 和 $y_{2}$ 是二元素向量 dydt 的项 y(1) 和 y(2)。

function dydt = vdp1(t,y)
%VDP1  Evaluate the van der Pol ODEs for mu = 1
%
%   See also ODE113, ODE23, ODE45.

%   Jacek Kierzenka and Lawrence F. Shampine
%   Copyright 1984-2014 The MathWorks, Inc.

dydt = [y(2); (1-y(1)^2)*y(2)-y(1)];

使用 ode78 函数、时间区间 [0 20] 和初始值 [2 0] 来解算该 ODE。生成的输出即为时间点 t 的列向量和解数组 y。y 中的每一行都与 t 的相应行中返回的时间相对应。y 的第一列与 $y_{1}$ 相对应，第二列与 $y_{2}$ 相对应。

[t,y] = ode78(@vdp1,[0 20],[2; 0]);

绘制 $y_{1}$ 和 $y_{2}$ 的解对 t 的图。

plot(t,y(:,1),'-o',t,y(:,2),'-o')
title('Solution of van der Pol Equation (\mu = 1) with ODE78');
xlabel('Time t');
ylabel('Solution y');
legend('y_1','y_2')

Figure contains an axes object. The axes object with title Solution of van der Pol Equation ( mu blank = blank 1 ) with ODE78, xlabel Time t, ylabel Solution y contains 2 objects of type line. These objects represent y_1, y_2.

向 ODE 函数传递额外的参数

打开实时脚本

ode78 仅适用于使用两个输入参量（t 和 y）的函数。但是，通过在函数外部定义参数并在指定函数句柄时传递这些参数，可以传入额外参数。

解算 ODE

$y^{''} = \frac{A}{B} t y .$

将该方程重写为一阶方程组可以得到

$\begin{array}{cl} y_{1}^{'} & = y_{2} \\ y_{2}^{'} & = \frac{A}{B} t y_{1} . \end{array}$

此示例末尾的局部函数 odefcn 将此方程组表示为接受四个输入参量（t、y、A 和 B）的函数。

function dydt = odefcn(t,y,A,B)
  dydt = zeros(2,1);
  dydt(1) = y(2);
  dydt(2) = (A/B)*t.*y(1);
end

使用 ode78 解算 ODE。指定函数句柄，使其将 A 和 B 的预定义值传递给 odefcn。

A = 1;
B = 2;
tspan = [0 5];
y0 = [0 0.01];
[t,y] = ode78(@(t,y) odefcn(t,y,A,B), tspan, y0);

绘制结果。

plot(t,y(:,1),'-o',t,y(:,2),'-.')

Figure contains an axes object. The axes object contains 2 objects of type line.

function dydt = odefcn(t,y,A,B)
  dydt = zeros(2,1);
  dydt(1) = y(2);
  dydt(2) = (A/B)*t.*y(1);
end

具有严格误差容限的 ODE

打开实时脚本

与 ode45 相比，ode113、ode78 和 ode89 求解器可以更好地求解具有严格误差容限的问题。这些求解器更胜一筹的常见情况是在轨道动力学问题中，这些问题的解曲线是平滑的且在求解器的每个时间步中都需要很高的准确度。

二体问题涉及两个相互作用的质点 m1 和 m2 在一个公共平面上沿轨道运动。在本示例中，一个质点明显大于另一个。以较重的天体为原点，运动方程为：

$\begin{array}{l} {x^{'}}^{'} = - x / r^{3} \\ {y^{'}}^{'} = - y / r^{3}, \end{array}$

其中

$r = \sqrt{x^{2} + y^{2}} .$

要求解该问题，首先使用以下替换公式转换为包含四个一阶 ODE 的方程组：

$\begin{array}{l} y_{1} = x \\ y_{2} = x^{'} \\ y_{3} = y \\ y_{4} = y^{'} . \end{array}$

替换之后生成的一阶方程组为：

$\begin{array}{l} {y_{1}}^{'} = y_{2} \\ {y_{2}}^{'} = - y_{1} / r^{3} \\ {y_{3}}^{'} = y_{4} \\ {y_{4}}^{'} = - y_{3} / r^{3} . \end{array}$

包含在此示例末尾的局部函数 twobodyode 为二体问题的方程组进行编码。

function dy = twobodyode(t,y)
% Two-body problem with one mass much larger than the other.
r = sqrt(y(1)^2 + y(3)^2);
dy = [y(2); 
     -y(1)/r^3;
      y(4);
     -y(3)/r^3];
end

使用 ode78 求解 ODE 方程组。对 RelTol 指定严格误差容限 1e-13，对 AbsTol 使用严格误差容限 1e-14。

opts = odeset('Reltol',1e-13,'AbsTol',1e-14,'Stats','on');
tspan = [0 10*pi];
y0 = [2 0 0 0.5];
[t,y] = ode78(@twobodyode, tspan, y0, opts);

341 successful steps
0 failed attempts
5797 function evaluations

plot(t,y)
legend('x','x''','y','y''','Location','SouthEast')
title('Position and Velocity Components')

Figure contains an axes object. The axes object with title Position and Velocity Components contains 4 objects of type line. These objects represent x, x', y, y'.

figure
plot(y(:,1),y(:,3),'-o',0,0,'ro')
axis equal
title('Orbit of Smaller Mass')

Figure contains an axes object. The axes object with title Orbit of Smaller Mass contains 2 objects of type line. One or more of the lines displays its values using only markers

与 ode45 相比，ode78 求解器能够通过更少的步骤和函数计算更快地获得解。

function dy = twobodyode(t,y)
% Two-body problem with one mass much larger than the other.
r = sqrt(y(1)^2 + y(3)^2);
dy = [y(2); 
    -y(1)/r^3;
    y(4);
    -y(3)/r^3];
end

输入参数

全部折叠

`odefun` — 要求解的函数
函数句柄

要求解的函数，指定为指向待积分器的句柄。

对于标量 t 和列向量 y 来说，函数 dydt = odefun(t,y) 必须返回数据类型为 single 或 double 的列向量 dydt，该列向量对应于 $f (t, y)$ 。odefun 必须同时接受输入参量 t 和 y，即使其中一个参量未在函数中使用也是如此。

例如，要解算 $y' = 5 y - 3$ ，请使用此函数：

function dydt = odefun(t,y)
dydt = 5*y-3;
end

对于方程组，odefun 的输出为向量。向量中的每个元素均为一个方程右侧的计算值。例如，考虑以下包含两个方程的方程组

$\begin{array}{l} y'_{1} = y_{1} + 2 y_{2} \\ y'_{2} = 3 y_{1} + 2 y_{2} \end{array}$

计算每个时间步下每个方程右侧值的函数为

function dydt = odefun(t,y)
dydt = zeros(2,1);
dydt(1) = y(1)+2*y(2);
dydt(2) = 3*y(1)+2*y(2);
end

有关如何为函数 odefun 提供其他参数的信息，请参阅参数化函数。

示例: @myFcn

数据类型: function_handle

`tspan` — 积分区间
向量

积分区间，指定为向量。至少，tspan 必须是指定初始时间和最终时间的二元素向量 [t0 tf]。要获取 t0 到 tf 之间的特定时间的解，请使用 [t0,t1,t2,...,tf] 形式的长向量。tspan 中的元素必须单调递增或单调递减。

求解器在初始时间 tspan(1) 施加由 y0 给出的初始条件，然后求 tspan(1) 到 tspan(end) 的积分：

如果 tspan 有两个元素 [t0 tf]，求解器将返回在该区间内的每个内部积分步计算的解。
如果 tspan 包含两个以上的元素，[t0,t1,t2,...,tf]，求解器将返回在给定点处计算的解。但是，求解器不会精确步进到 tspan 中指定的每个点。此时，求解器使用自己的内部积分步来计算解，然后在 tspan 中请求的各点处计算解。在指定点处生成的解与在每个内部积分步计算的解具有相同的准确度级别。
指定多个中间点对计算效率影响甚微，但对于大型系统可能会影响内存管理。

求解器使用 tspan 的值计算 InitialStep 和 MaxStep 的合适值：

如果 tspan 包含多个中间点 [t0,t1,t2,...,tf]，则指定的点表示了问题的规模，这可能影响求解器使用的 InitialStep 的值。因此，根据您是将 tspan 指定为二元素向量还是包含中间点的向量，求解器获得的解可能有所不同。
tspan 中的初始值和最终值用于计算最大步长 MaxStep。因此，更改 tspan 中的初始值或最终值可能导致求解器使用不同步长序列，从而可能会更改解。

示例: [1 10]

示例: [1 3 5 7 9 10]

数据类型: single | double

`y0` — 初始条件
向量

初始条件，指定为向量。y0 的长度必须与 odefun 的向量输出相同，使 y0 为 odefun 中定义的每个方程包含一个初始条件。

数据类型: single | double

`options` — options 结构体
结构体数组

options 结构体，指定为结构体数组。使用 odeset 函数创建或修改 options 结构体。有关与每个求解器兼容的选项列表，请参阅 ODE 选项摘要。

示例: options = odeset('RelTol',1e-5,'Stats','on','OutputFcn',@odeplot) 指定 1e-5 的相对误差容限、打开求解器统计信息的显示，并指定输出函数 @odeplot 在计算时绘制解。

数据类型: struct

输出参量

全部折叠

`t` — 求值点
列向量

计算点，以列向量形式返回。

如果 tspan 包含两个元素 [t0 tf]，则 t 包含用于执行积分的内部计算点。
如果 tspan 包含两个以上元素，则 t 与 tspan 相同。

`y` — 解
数组

解，以数组形式返回。y 中的每一行都与 t 的相应行中返回的值处的解相对应。

`te` — 事件的时间
列向量

事件的时间，以列向量形式返回。te 中的事件时间对应于 ye 中返回的解，而 ie 指定发生了哪个事件。

`ye` — 事件时间处的解
数组

事件时间的解，以数组形式返回。te 中的事件时间对应于 ye 中返回的解，而 ie 指定发生了哪个事件。

`ie` — 触发的事件函数的索引
列向量

触发的事件函数的索引，以列向量形式返回。te 中的事件时间对应于 ye 中返回的解，而 ie 指定发生了哪个事件。

`sol` — 用于计算的结构体
结构体数组

用于计算的结构体，以结构体数组形式返回。此结构体与 deval 函数一起使用，用于计算区间 [t0 tf] 内任何点的解。sol 结构体数组始终包括下列字段：

结构体字段	描述
`sol.x`	求解器选择的步的行向量。
`sol.y`	解。每列 `sol.y(:,i)` 包含时间 `sol.x(i)` 处的解。
`sol.solver`	求解器名称。

此外，如果指定了 odeset 的 Events 选项并且检测到事件，则 sol 还包括下列字段：

结构体字段	描述
`sol.xe`	事件发生的点。`sol.xe(end)` 包含终止事件（如果有）的确切点。
`sol.ye`	与 `sol.xe` 中的事件相对应的解。
`sol.ie`	`Events` 选项中指定的函数所返回的向量的索引。这些值指示求解器检测到的事件。

算法

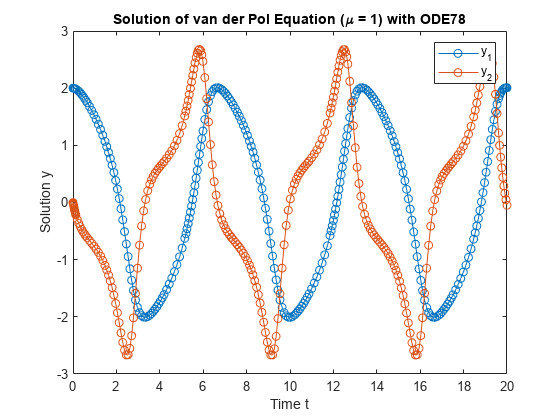
ode78 是 Verner 的“最高效”的 7 阶连续外推龙格-库塔 8(7) 法的一种实现。解的精度提升到了 8 阶。7 阶连续外推需要对 odefun 进行四次额外计算，但仅限于需要插值的步。

参考

[1] Verner, J. H. “Numerically Optimal Runge–Kutta Pairs with Interpolants.” Numerical Algorithms 53, no. 2–3 (March 2010): 383–396. https://doi.org/10.1007/s11075-009-9290-3.

扩展功能

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

所有 odeset 选项参量都必须为常量。
代码生成不支持在 options 结构体中使用常量质量矩阵。需以函数形式提供质量矩阵。
必须提供至少两个输出参量 T 和 Y。
输入类型必须为同类 - 全部为双精度或全部为单精度。
必须启用可变大小支持。当 tspan 有两个元素或当您使用事件函数时，代码生成需要动态分配内存。

版本历史记录

在 R2021b 中推出

另请参阅

ode23 | ode45 | ode89 | ode113 | odeset | odeget | deval | odextend

ode78

语法

说明

示例

具有一个解分量的 ODE

解算非刚性方程

向 ODE 函数传递额外的参数

具有严格误差容限的 ODE

输入参数

odefun — 要求解的函数 函数句柄

tspan — 积分区间 向量

y0 — 初始条件 向量

options — options 结构体 结构体数组

输出参量

t — 求值点 列向量

y — 解 数组

te — 事件的时间 列向量

ye — 事件时间处的解 数组

ie — 触发的事件函数的索引 列向量

sol — 用于计算的结构体 结构体数组

算法

参考

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

版本历史记录

另请参阅

主题

WeChat

`odefun` — 要求解的函数
函数句柄

`tspan` — 积分区间
向量

`y0` — 初始条件
向量

`options` — options 结构体
结构体数组

`t` — 求值点
列向量

`y` — 解
数组

`te` — 事件的时间
列向量

`ye` — 事件时间处的解
数组

`ie` — 触发的事件函数的索引
列向量

`sol` — 用于计算的结构体
结构体数组

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。