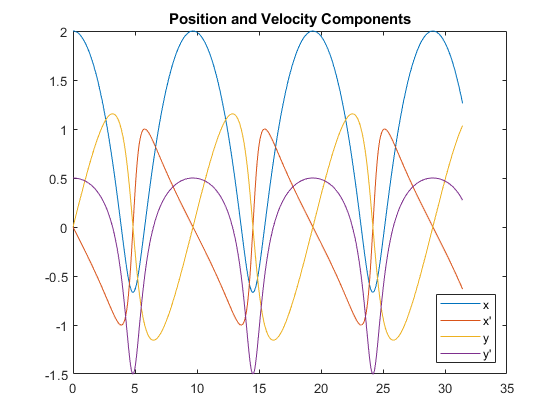
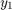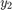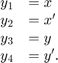ode113
求解非刚性微分方程 - 变阶方法
语法
说明
sol = ode113(___)deval 结合使用来计算区间 [t0 tf] 中任意点位置的解。您可以使用上述语法中的任何输入参量组合。
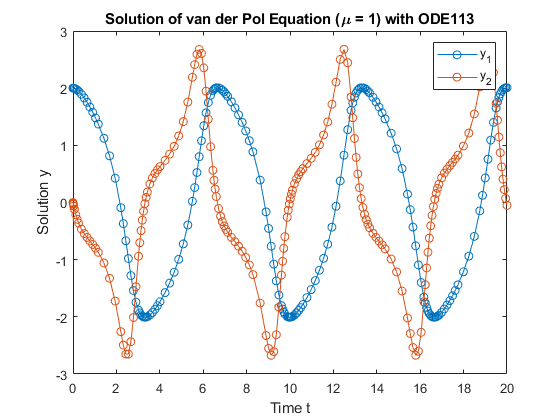
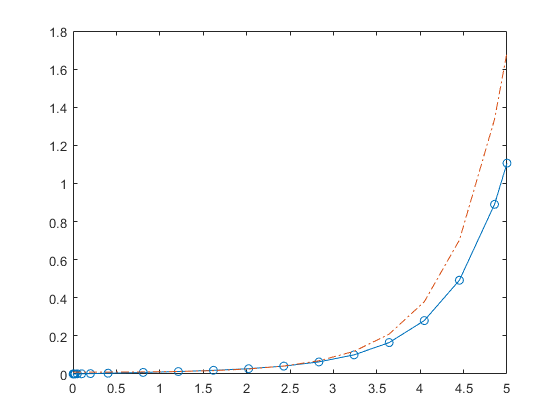
示例
输入参数
输出参量
算法
ode113 是一个变步长、可变阶次 (VSVO) 的 Adams-Bashforth-Moulton PECE 求解器,阶次从 1 到 13。使用的最高阶次似乎是 12,但 13 阶公式用于形成误差估计,并且该函数会进行局部外插,以便继续完成第 13 阶的积分。
在容差较严格或 ODE 函数的计算开销太大的情况下,ode113 可能比 ode45 更加有效。ode113 是一个多步求解器,它通常需要前面几个时间点的解才能计算出当前解 [1] [2]。
参考
[1] Shampine, L. F. and M. K. Gordon, Computer Solution of Ordinary Differential Equations: the Initial Value Problem, W. H. Freeman, San Francisco, 1975.
[2] Shampine, L. F. and M. W. Reichelt, “The MATLAB ODE Suite,” SIAM Journal on Scientific Computing, Vol. 18, 1997, pp. 1–22.
版本历史记录
在 R2006a 之前推出