求解具有多个初始条件的 ODE 方程组

打开实时脚本

此示例比较求解具有多组初始条件的常微分方程组的两种方法。这些方法是：

使用 for 循环执行多次仿真，每组初始条件对应一次仿真。此方法使用起来很简单，但对于大型方程组不能实现最优性能。
向量化 ODE 函数，以同时针对各组初始条件求解方程组。对于大型方程组来说，这是更快的方法，但需要重写 ODE 函数以便正确地重构输入。

用于说明这些方法的方程是众所周知的 Lotka-Volterra 方程，它们是描述捕食者和猎物种群的一阶非线性微分方程。

问题描述

Lotka-Volterra 方程是由两个一阶非线性 ODE 组成的方程组，用于描述生物系统中捕食者和猎物的种群。随着时间的推移，捕食者和猎物的数量会根据方程发生变化

$\begin{array}{l} \frac{dx}{dt} = α x - β xy, \\ \frac{dy}{dt} = δ xy - γ y . \end{array}$

这些方程中的变量包括

$x$ 是猎物的种群大小
$y$ 是捕食者的种群大小
$t$ 是时间
$α$ 、 $β$ 、 $δ$ 和 $γ$ 是描述两个物种之间交互的常量参数。此示例使用参数值 $α = γ = 1$ 、 $β = 0.01$ 和 $δ = 0.02$ 。

对于此问题， $x$ 和 $y$ 的初始值是初始种群大小。求解这些方程，就能提供关于物种交互时种群如何随时间变化的信息。

求解具有一个初始条件的方程

要在 MATLAB® 中求解 Lotka-Volterra 方程，请编写一个函数来对方程进行编码，指定积分的时间区间，并指定初始条件。然后，您可以使用一个 ODE 求解器（如 ode45）对方程组随时间的变化进行仿真。

对方程进行编码的函数是

function dpdt = lotkaODE(t,p)
% LOTKA Lotka-Volterra predator-prey model
delta = 0.02;
beta = 0.01;

dpdt = [p(1) .* (1 - beta*p(2));
        p(2) .* (-1 + delta*p(1))];
end

（该函数作为局部函数包含在示例的末尾。）

由于方程组中有两个方程，dpdt 是向量，其中每个元素对应一个方程。此外，对于每个解分量，解向量 p 中都有一个对应的元素：p(1) 表示原始方程中的 $x$ ，p(2) 表示原始方程中的 $y$ 。

接下来，将积分的时间区间指定为 $[0, 15]$ ，并将 $x$ 和 $y$ 的初始种群大小设置为 50。

t0 = 0;
tfinal = 15;
p0 = [50; 50];

通过指定 ODE 函数、时间跨度和初始条件，用 ode45 求解方程组。绘制结果种群对时间的图。

[t,p] = ode45(@lotkaODE,[t0 tfinal],p0);
plot(t,p)
title('Predator/Prey Populations Over Time')
xlabel('t')
ylabel('Population')
legend('Prey','Predators')

Figure contains an axes object. The axes object with title Predator/Prey Populations Over Time, xlabel t, ylabel Population contains 2 objects of type line. These objects represent Prey, Predators.

由于解呈现周期性，在相位图中绘制各解之间相对关系的图。

plot(p(:,1),p(:,2))
title('Phase Plot of Predator/Prey Populations')
xlabel('Prey')
ylabel('Predators')

Figure contains an axes object. The axes object with title Phase Plot of Predator/Prey Populations, xlabel Prey, ylabel Predators contains an object of type line.

所得的图显示针对给定初始种群大小的解。要求解针对不同初始种群大小的方程，请更改 p0 中的值，然后重新运行仿真。然而，此方法一次只能针对一个初始条件求解方程。接下来的两节说明针对许多不同初始条件求解的方法。

方法 1：用 `for-` 循环计算多个初始条件

求解具有多个初始条件的 ODE 方程组的最简单方法是使用 for 循环。此方法使用与单一初始条件方法相同的 ODE 函数，但 for 循环会自动执行求解过程。

例如，您可以将 $x$ 的初始种群大小保持为 50，并使用 for 循环使 $y$ 的初始种群大小在 10 到 400 之间变化。为 y0 创建一个种群大小向量，然后遍历这些值以针对每组初始条件求解方程。用所有迭代的结果绘制一个相位图。

y0 = 10:10:400;
for k = 1:length(y0)
    [t,p] = ode45(@lotkaODE,[t0 tfinal],[50 y0(k)]);
    plot(p(:,1),p(:,2))
    hold on
end
title('Phase Plot of Predator/Prey Populations')
xlabel('Prey')
ylabel('Predators')
hold off

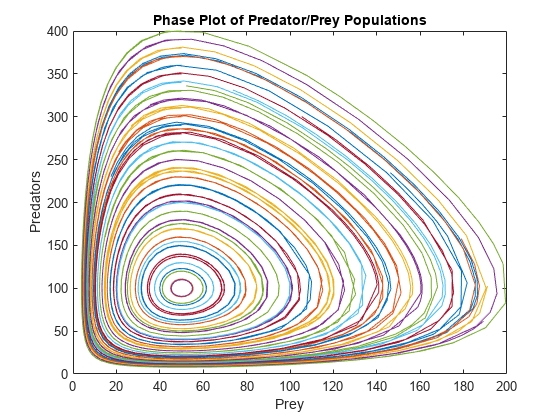
Figure contains an axes object. The axes object with title Phase Plot of Predator/Prey Populations, xlabel Prey, ylabel Predators contains 40 objects of type line.

该相位图显示不同初始条件组的所有计算结果。

方法 2：用向量化 ODE 函数计算多个初始条件

求解多初始条件的 ODE 方程组的另一种方法是重写 ODE 函数，以便同时求解所有方程。其实现步骤如下：

将所有初始条件作为一个矩阵提供给 ode45。该矩阵的大小为 s×n，其中 s 是解分量数目，n 是要求解的方程的初始条件的数目。矩阵中的每列表示方程组的一组完整初始条件。
ODE 函数必须接受额外输入参数 n，即初始条件的数目。
在 ODE 函数中，求解器将解分量 p 作为列向量传递。ODE 函数必须将向量重构为 s×n 大小的矩阵。这样，矩阵的每行都包含每个变量的所有初始条件。
ODE 函数必须求解向量化格式的方程，以便表达式接受向量作为解分量。换句话说，f(t,[y1 y2 y3 ...]) 必须返回 [f(t,y1) f(t,y2) f(t,y3) ...]。
最后，ODE 函数必须将其输出重构回向量，以便 ODE 求解器从每次函数调用接收一个向量。

如果您按照这些步骤操作，则 ODE 求解器可以使用解分量的向量来求解方程组，而 ODE 函数将向量重构为矩阵，并针对所有初始条件求解每个解分量。结果是，您可以在一次仿真中针对所有初始条件求解方程组。

要对 Lotka-Volterra 方程组实现此方法，首先要找到初始条件的数量 n，然后构成一个初始条件矩阵。

n = length(y0);
p0_all = [50*ones(n,1) y0(:)]';

接下来，重写 ODE 函数，使其接受 n 作为输入。使用 n 将解向量重构为矩阵，然后求解向量化方程组，并将输出重构回向量。经修改后执行这些任务的 ODE 函数是

function dpdt = lotkasystem(t,p,n)
%LOTKA  Lotka-Volterra predator-prey model for system of inputs p.
delta = 0.02;
beta = 0.01;

% Change the size of p to be: Number of equations-by-number of initial
% conditions.
p = reshape(p,[],n);

% Write equations in vectorized form.
dpdt = [p(1,:) .* (1 - beta*p(2,:)); 
        p(2,:) .* (-1 + delta*p(1,:))];

% Linearize output.
dpdt = dpdt(:);
end

使用 ode45 针对所有初始条件求解方程组。由于 ode45 要求 ODE 函数接受两个输入，请使用匿名函数将 n 的值从工作区传入 lotkasystem。

[t,p] = ode45(@(t,p) lotkasystem(t,p,n),[t0 tfinal],p0_all);

将输出向量重构为 (numTimeSteps*s)×n 大小的矩阵。输出 p(:,k) 的每列都包含针对一组初始条件的解。绘制解分量的相位图。

p = reshape(p,[],n);
nt = length(t);
for k = 1:n
    plot(p(1:nt,k),p(nt+1:end,k))
    hold on
end
title('Predator/Prey Populations Over Time')
xlabel('t')
ylabel('Population')
hold off

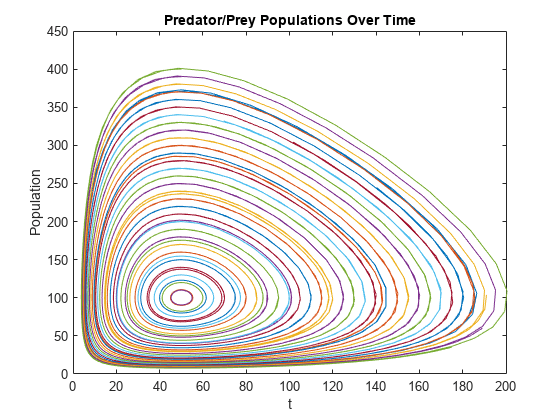
Figure contains an axes object. The axes object with title Predator/Prey Populations Over Time, xlabel t, ylabel Population contains 40 objects of type line.

结果与通过 for 循环方法获得的值类似。但是，您应牢记向量化解方法的一些特性：

计算的解可能与从单个初始输入计算的解略有不同。出现差异是因为 ODE 求解器对整个方程组应用范数检查来计算时间步的大小，因此解的时间步进行为略有不同。时间步的变化通常不会影响解的精确度，而是影响计算解的时间点。
对于自动计算方程组的数值雅可比矩阵的刚性 ODE 求解器（ode15s、ode23s、ode23t、ode23tb），使用 odeset 的 JPattern 选项指定雅可比矩阵的分块对角稀疏模式可以提高计算效率。分块对角雅可比矩阵是重写的 ODE 函数对输入重构后产生的。

比较计时结果

使用 timeit 对上述每种方法进行计时。求解含一组初始条件的方程的计时结果将作为基线值来衡量各方法。

% Time one IC
baseline = timeit(@() ode45(@lotkaODE,[t0 tfinal],p0),2);

% Time for-loop
for k = 1:length(y0)
    loop_timing(k) = timeit(@() ode45(@lotkaODE,[t0 tfinal],[50 y0(k)]),2);
end
loop_timing = sum(loop_timing);

% Time vectorized fcn
vectorized_timing = timeit(@() ode45(@(t,p) lotkasystem(t,p,n),[t0 tfinal],p0_all),2);

创建一个计时结果表。将所有结果乘以 1e3，以毫秒为单位表示时间。其中一列为每个解的平均用时，该值通过将计时时间除以初始条件数目求得。

TimingTable = table(1e3.*[baseline; loop_timing; vectorized_timing], 1e3.*[baseline; loop_timing/n; vectorized_timing/n],...
    'VariableNames',{'TotalTime (ms)','TimePerSolution (ms)'},'RowNames',{'One IC','Multi ICs: For-loop', 'Mult ICs: Vectorized'})

TimingTable=3×2 table
                            TotalTime (ms)    TimePerSolution (ms)
                            ______________    ____________________

    One IC                     0.40718              0.40718       
    Multi ICs: For-loop         11.967              0.29916       
    Mult ICs: Vectorized        1.6168              0.04042

TimePerSolution 列显示向量化方法是三种方法中最快的。

局部函数

此处列出了 ode45 为计算解而调用的局部函数。

function dpdt = lotkaODE(t,p)
% LOTKA Lotka-Volterra predator-prey model
delta = 0.02;
beta = 0.01;

dpdt = [p(1) .* (1 - beta*p(2));
        p(2) .* (-1 + delta*p(1))];
end
%------------------------------------------------------------------
function dpdt = lotkasystem(t,p,n)
%LOTKA  Lotka-Volterra predator-prey model for system of inputs p.
delta = 0.02;
beta = 0.01;

% Change the size of p to be: Number of equations-by-number of initial
% conditions.
p = reshape(p,[],n);

% Write equations in vectorized form.
dpdt = [p(1,:) .* (1 - beta*p(2,:)); 
        p(2,:) .* (-1 + delta*p(1,:))];

% Linearize output.
dpdt = dpdt(:);
end

另请参阅

ode45 | odeset