求解具有不连续性的 PDE

此示例说明如何求解涉及物质界面的 PDE。物质界面使得问题在 $x = 0.5$ 处具有不连续点，初始条件在右边界 $x = 1$ 处具有不连续点。

以如下分段 PDE 为例

${\begin{matrix} \frac{\partial u}{\partial t} = x^{- 2} \frac{\partial}{\partial x} (x^{2} 5 \frac{\partial u}{\partial x}) - 1000 e^{u} & (0 \leq x \leq 0.5) \\ \frac{\partial u}{\partial t} = x^{- 2} \frac{\partial}{\partial x} (x^{2} \frac{\partial u}{\partial x}) - e^{u} & (0.5 \leq x \leq 1) \end{matrix}$

初始条件为

$\begin{array}{l} u (x, 0) = 0 (0 \leq x < 1), \\ u (1, 0) = 1 (x = 1) . \end{array}$

边界条件为

$\begin{array}{l} \frac{\partial u}{\partial x} = 0 (x = 0), \\ u (1, t) = 1 (x = 1) . \end{array}$

要在 MATLAB® 中求解该方程，您需要对方程、初始条件和边界条件编写代码，然后在调用求解器 pdepe 之前选择合适的解网格。您可以将所需的函数作为局部函数包含在文件末尾（如本处所示），或者将它们作为单独的命名文件保存在 MATLAB 路径上的目录中。

编写方程代码

在编写方程代码之前，您需要确保它的形式符合 pdepe 求解器的要求。pdepe 所需的标准形式是

$c (x, t, u, \frac{\partial u}{\partial x}) \frac{\partial u}{\partial t} = x^{- m} \frac{\partial}{\partial x} (x^{m} f (x, t, u, \frac{\partial u}{\partial x})) + s (x, t, u, \frac{\partial u}{\partial x})$ .

在本例中，PDE 采用了正确形式，因此您可以读取系数的值。

通量项 $f (x, t, u, \frac{\partial u}{\partial x})$ 和源项 $s (x . t, u, \frac{\partial u}{\partial x})$ 的值根据 $x$ 的值而变化。系数是：

$m = 2$

$c (x, t, u, \frac{\partial u}{\partial x}) = 1$

${\begin{matrix} f (x, t, u, \frac{\partial u}{\partial x}) = 5 \frac{\partial u}{\partial x} & (0 \leq x \leq 0.5) \\ f (x, t, u, \frac{\partial u}{\partial x}) = \frac{\partial u}{\partial x} & (0.5 \leq x \leq 1) \end{matrix}$

${\begin{matrix} s (x, t, u, \frac{\partial u}{\partial x}) = - 1000 e^{u} & (0 \leq x \leq 0.5) \\ s (x, t, u, \frac{\partial u}{\partial x}) = - e^{u} & (0.5 \leq x \leq 1) \end{matrix}$

现在，您可以创建一个函数以编写方程代码。该函数应具有签名 [c,f,s] = pdex2pde(x,t,u,dudx)：

x 是独立的空间变量。
t 是独立的时间变量。
u 是关于 x 和 t 微分的因变量。
dudx 是偏空间导数 $\partial u / \partial x$ 。
输出 c、f 和 s 对应于 pdepe 所需的标准 PDE 形式中的系数。根据输入变量 x、t、u 和 dudx 对这些系数编写代码。

因此，此示例中的方程可以由以下函数表示：

function [c,f,s] = pdex2pde(x,t,u,dudx)
c = 1;
if x <= 0.5
    f = 5*dudx;
    s = -1000*exp(u);
else
    f = dudx;
    s = -exp(u);
end
end

（注意：所有函数都作为局部函数包含在示例的末尾。）

编写初始条件代码

接下来，编写一个返回初始条件的函数。初始条件应用在第一个时间值处，并为 $x$ 的任何值提供 $u (x, t_{0})$ 的值。使用函数签名 u0 = pdex2ic(x) 编写函数。

初始条件为

$\begin{array}{l} u (x, 0) = 0 (0 \leq x < 1), \\ u (1, 0) = 1 (x = 1) . \end{array}$

对应的函数是

function u0 = pdex2ic(x)
if x < 1
    u0 = 0;
else
    u0 = 1;
end
end

编写边界条件代码

现在，编写一个计算边界条件的函数。对于区间 $a \leq x \leq b$ 上的问题，边界条件应用于所有 t 以及 $x = a$ 或 $x = b$ 的情形。求解器所需的边界条件的标准形式是

$p (x, t, u) + q (x, t) f (x, t, u, \frac{\partial u}{\partial x}) = 0 .$

由于此示例具有球面对称性 ( $m = 2$ )，pdepe 求解器会自动强制执行左边界条件以约束在原点的解，并忽略在边界函数中为左边界指定的任何条件。因此，对于左边界条件，您可以指定 $p_{L} = q_{L} = 0$ 。对于右边界条件，您可以用标准形式重写边界条件，并读取 $p_{R}$ 和 $q_{R}$ 的系数值。

对于 $x = 1$ ，方程为 $u (1, t) = 1 \to (u - 1) + 0 \cdot \frac{\partial u}{\partial x} = 0$ 。系数是：

$p_{R} (1, t, u) = u - 1$
$q_{R} (1, t) = 0$

边界函数应使用函数签名 [pl,ql,pr,qr] = pdex2bc(xl,ul,xr,ur,t)：

对于左边界，输入 xl 和 ul 对应于 u 和 x。
对于右边界，输入 xr 和 ur 对应于 u 和 x。
t 是独立的时间变量。
对于左边界，输出 pl 和 ql 对应于 $p_{L} (x, t, u)$ 和 $q_{L} (x, t)$ （对于此问题， $x = 0$ ）。
对于右边界，输出 pr 和 qr 对应于 $p_{R} (x, t, u)$ 和 $q_{R} (x, t)$ （对于此问题， $x = 1$ ）。

此示例中的边界条件由以下函数表示：

function [pl,ql,pr,qr] = pdex2bc(xl,ul,xr,ur,t)
pl = 0; 
ql = 0; 
pr = ur - 1;
qr = 0;
end

选择解网格

空间网格应包括 $x = 0.5$ 附近的几个值以表示不连续界面，并包括 $x = 1$ 附近的点，因为在该点上具有不一致的初始值 ( $u (1, 0) = 1$ ) 和边界值 ( $u (1, t) = 0$ )。对于较小的 $t$ ，解的变化很快，因此请使用可以解析这种急剧变化的时间步。

x = [0 0.1 0.2 0.3 0.4 0.45 0.475 0.5 0.525 0.55 0.6 0.7 0.8 0.9 0.95 0.975 0.99 1];
t = [0 0.001 0.005 0.01 0.05 0.1 0.5 1];

求解方程

最后，使用对称性值 m、PDE 方程、初始条件、边界条件以及 x 和 t 的网格来求解方程。

m = 2;
sol = pdepe(m,@pdex2pde,@pdex2ic,@pdex2bc,x,t);

pdepe 以三维数组 sol 形式返回解，其中 sol(i,j,k) 是在 t(i) 和 x(j) 处计算的解 $u_{k}$ 的第 k 个分量的逼近值。sol 的大小是 length(t)×length(x)×length(u0)，因为 u0 为每个解分量指定初始条件。对于此问题，u 只有一个分量，因此 sol 是 8×18 矩阵，但通常您可以使用命令 u = sol(:,:,k) 提取第 k 个解分量。

从 sol 中提取第一个解分量。

u = sol(:,:,1);

对解进行绘图

创建在 $x$ 和 $t$ 的所选网格点上绘制的解 $u$ 的曲面图。由于 $m = 2$ 问题是在具有球面对称性的球面几何中提出的，因此解仅在径向 $x$ 方向上变化。

surf(x,t,u)
title('Numerical solution with nonuniform mesh')
xlabel('Distance x')
ylabel('Time t')
zlabel('Solution u')

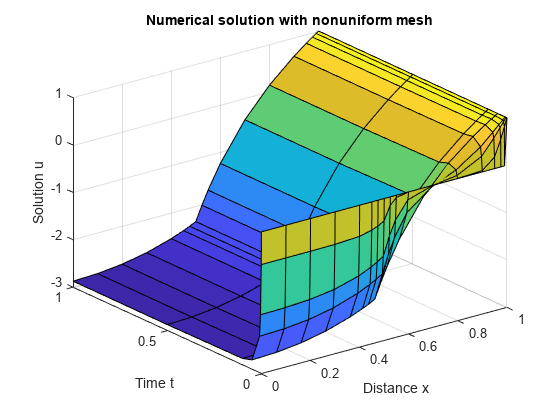
Figure contains an axes object. The axes object with title Numerical solution with nonuniform mesh, xlabel Distance x, ylabel Time t contains an object of type surface.

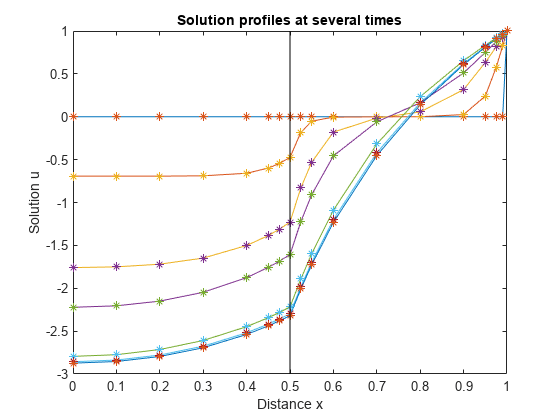
现在，只需绘制 $x$ 和 $u$ 即可获得曲面图中等高线的侧视图。在 $x = 0.5$ 处添加一条线，以突出材料接口的效果。

plot(x,u,x,u,'*')
line([0.5 0.5], [-3 1], 'Color', 'k')
xlabel('Distance x')
ylabel('Solution u')
title('Solution profiles at several times')

Figure contains an axes object. The axes object with title Solution profiles at several times, xlabel Distance x, ylabel Solution u contains 17 objects of type line. One or more of the lines displays its values using only markers

局部函数

此处列出 PDE 求解器 pdepe 为计算解而调用的局部辅助函数。您也可以将这些函数作为它们自己的文件保存在 MATLAB 路径上的目录中。

function [c,f,s] = pdex2pde(x,t,u,dudx) % Equation to solve
c = 1;
if x <= 0.5
    f = 5*dudx;
    s = -1000*exp(u);
else
    f = dudx;
    s = -exp(u);
end
end
%----------------------------------------------
function u0 = pdex2ic(x) %Initial conditions
if x < 1
    u0 = 0;
else
    u0 = 1;
end
end
%----------------------------------------------
function [pl,ql,pr,qr] = pdex2bc(xl,ul,xr,ur,t) % Boundary conditions
pl = 0;
ql = 0;
pr = ur - 1;
qr = 0;
end
%----------------------------------------------

另请参阅

pdepe