求解 PDE 并计算偏导数
此示例说明如何求解一个晶体管偏微分方程 (PDE),并使用结果获得偏导数,这是求解更大型问题的一部分。
以如下 PDE 为例
此方程出现在晶体管理论 [1] 中, 是描述 PNP 晶体管基极中过剩电荷载流子(或空穴)浓度的函数。 和 是物理常量。该公式在区间 上对于时间 成立。
初始条件包括常量 ,由下式给出
该问题具有由下式给出的边界条件
对于固定 ,方程 的解将过剩电荷的坍塌描述为 。这种坍塌产生一种电流,称为发射极放电电流,它还有另一个常量 :
由于在 和 时, 处的边界值不一致,该公式对 有效。由于 PDE 对 有闭型级数解,您可以通过解析方式和数值方式计算发射极放电电流,并对结果进行比较。
要在 MATLAB® 中求解此问题,您需要对 PDE、方程、初始条件和边界条件编写代码,然后在调用求解器 pdepe 之前选择合适的解网格。您可以将所需的函数作为局部函数包含在文件末尾(如本处所示),或者将它们作为单独的命名文件保存在 MATLAB 路径上的目录中。
定义物理常量
要跟踪物理常量,请创建一个结构体数组,其中每个常量都有一个对应的字段。当您稍后为方程、初始条件和边界条件定义函数时,可以将此结构体作为额外的参量传入,以便函数可以访问常量。
C.L = 1; C.D = 0.1; C.eta = 10; C.K = 1; C.Ip = 1;
编写方程代码
在编写方程代码之前,您需要确保它的形式符合 pdepe 求解器的要求:
此形式的 PDE 为
因此,方程中的系数的值是
(没有角对称性的笛卡尔坐标)
现在,您可以创建一个函数以编写方程代码。该函数应具有签名 [c,f,s] = transistorPDE(x,t,u,dudx,C):
x是独立的空间变量。t是独立的时间变量。u是关于x和t微分的因变量。dudx是偏空间导数 。C是包含物理常量的额外输入。输出
c、f和s对应于pdepe所需的标准 PDE 形式中的系数。
因此,此示例中的方程可以由以下函数表示:
function [c,f,s] = transistorPDE(x,t,u,dudx,C) D = C.D; eta = C.eta; L = C.L; c = 1; f = D*dudx; s = -(D*eta/L)*dudx; end
(注意:所有函数都作为局部函数包含在示例的末尾。)
代码初始条件
接下来,编写一个返回初始条件的函数。初始条件应用在第一个时间值处,并为 的任何值提供 的值。使用函数签名 u0 = transistorIC(x,C) 编写函数。
初始条件为
对应的函数是
function u0 = transistorIC(x,C) K = C.K; L = C.L; D = C.D; eta = C.eta; u0 = (K*L/D)*(1 - exp(-eta*(1 - x/L)))/eta; end
编写边界条件代码
现在,编写一个计算边界条件 的函数。对于在区间 上提出的问题,边界条件应用于所有 以及 或 。求解器所需的边界条件的标准形式是
以这种形式编写的此问题的边界条件是
- 对于 ,方程为 系数为:
- 同样,对于 ,方程为 系数为:
边界函数应使用函数签名 [pl,ql,pr,qr] = transistorBC(xl,ul,xr,ur,t):
对于左边界,输入 x
l和 ul对应于 和 。对于右边界,输入
xr和ur对应于 和 。t是独立的时间变量。对于左边界,输出
pl和ql对应于 和 (对于此问题,)。对于右边界,输出
pr和qr对应于 和 (对于此问题,)。
此示例中的边界条件由以下函数表示:
function [pl,ql,pr,qr] = transistorBC(xl,ul,xr,ur,t) pl = ul; ql = 0; pr = ur; qr = 0; end
选择解网格
解网格定义 和 的值,求解器基于它们来计算解。由于此问题的解变化很快,请使用一个相对精细的网格,其中包含 50 个位于 区间中的空间点和 50 个位于 区间中的时间点。
x = linspace(0,C.L,50); t = linspace(0,1,50);
求解方程
最后,使用对称性值 、PDE 方程、初始条件、边界条件以及 和 的网格来求解方程。由于 pdepe 需要 PDE 函数使用四个输入、初始条件函数使用一个输入,请创建函数句柄,将由物理常量组成的结构体作为额外输入来传入。
m = 0; eqn = @(x,t,u,dudx) transistorPDE(x,t,u,dudx,C); ic = @(x) transistorIC(x,C); sol = pdepe(m,eqn,ic,@transistorBC,x,t);
pdepe 以三维数组 sol 形式返回解,其中 sol(i,j,k) 是在 t(i) 和 x(j) 处计算的解 的第 k 个分量的逼近值。对于此问题,u 只有一个分量,但通常您可以使用命令 u = sol(:,:,k) 提取第 k 个解分量。
u = sol(:,:,1);
对解进行绘图
创建在 和 的所选网格点上绘制的解 的曲面图。
surf(x,t,u) title('Numerical Solution (50 mesh points)') xlabel('Distance x') ylabel('Time t') zlabel('Solution u(x,t)')
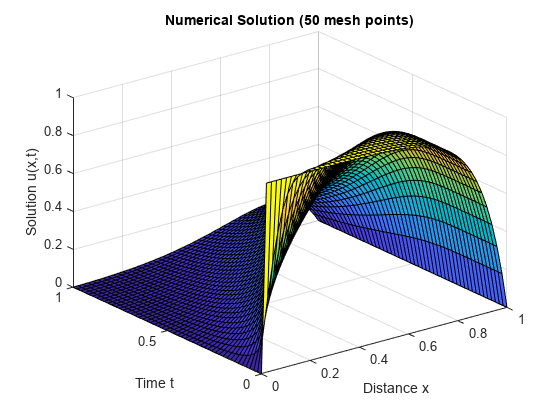
现在,只需绘制 和 即可获得曲面图中等高线的侧视图。
plot(x,u) xlabel('Distance x') ylabel('Solution u(x,t)') title('Solution profiles at several times')
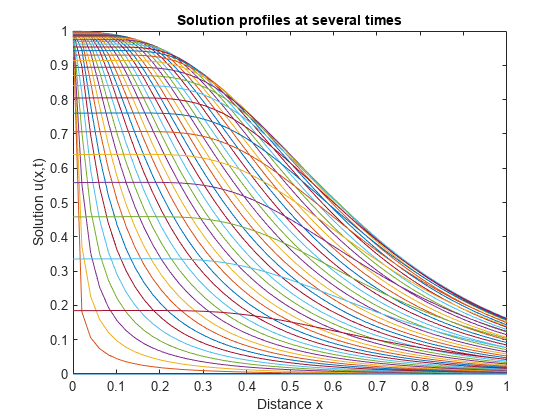
计算发射极放电电流
使用 的级数解,发射极放电电流可以表示为无穷级数 [1]:
编写一个函数,以使用级数中的 40 个项计算 的解析解。唯一的变量是时间,但要将常量结构体指定为函数的另一个输入。
function It = serex3(t,C) % Approximate I(t) by series expansion. Ip = C.Ip; eta = C.eta; D = C.D; L = C.L; It = 0; for n = 1:40 % Use 40 terms m = (n*pi)^2 + 0.25*eta^2; It = It + ((n*pi)^2 / m)* exp(-(D/L^2)*m*t); end It = 2*Ip*((1 - exp(-eta))/eta)*It; end
使用 pdepe 计算的 的数值解,您还可以通过以下方程计算在 处的 的数值逼近
计算 的解析解和数值解,并对结果绘图。使用 pdeval 计算 在 处的值。
nt = length(t); I = zeros(1,nt); seriesI = zeros(1,nt); iok = 2:nt; for j = iok % At time t(j), compute du/dx at x = 0. [~,I(j)] = pdeval(m,x,u(j,:),0); seriesI(j) = serex3(t(j),C); end % Numeric solution has form I(t) = (I_p*D/K)*du(0,t)/dx I = (C.Ip*C.D/C.K)*I; plot(t(iok),I(iok),'o',t(iok),seriesI(iok)) legend('From PDEPE + PDEVAL','From series') title('Emitter discharge current I(t)') xlabel('Time t')
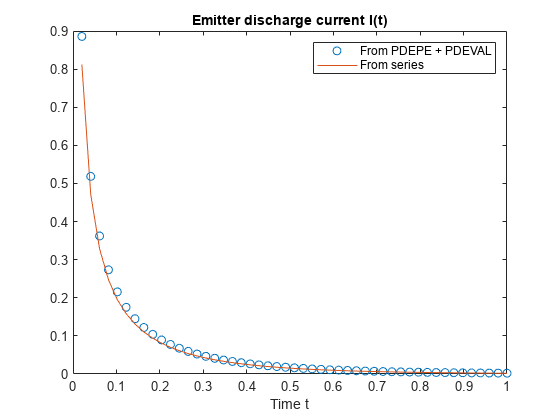
结果相当吻合。通过使用更精细的解网格,您可以进一步改进 pdepe 得出的数值结果。
局部函数
此处列出 PDE 求解器 pdepe 为计算解而调用的局部辅助函数。您也可以将这些函数作为它们自己的文件保存在 MATLAB 路径上的目录中。
function [c,f,s] = transistorPDE(x,t,u,dudx,C) % Equation to solve D = C.D; eta = C.eta; L = C.L; c = 1; f = D*dudx; s = -(D*eta/L)*dudx; end % ---------------------------------------------------- function u0 = transistorIC(x,C) % Initial condition K = C.K; L = C.L; D = C.D; eta = C.eta; u0 = (K*L/D)*(1 - exp(-eta*(1 - x/L)))/eta; end % ---------------------------------------------------- function [pl,ql,pr,qr] = transistorBC(xl,ul,xr,ur,t) % Boundary conditions pl = ul; ql = 0; pr = ur; qr = 0; end % ---------------------------------------------------- function It = serex3(t,C) % Approximate I(t) by series expansion. Ip = C.Ip; eta = C.eta; D = C.D; L = C.L; It = 0; for n = 1:40 % Use 40 terms m = (n*pi)^2 + 0.25*eta^2; It = It + ((n*pi)^2 / m)* exp(-(D/L^2)*m*t); end It = 2*Ip*((1 - exp(-eta))/eta)*It; end % ----------------------------------------------------
参考
[1] Zachmanoglou, E.C. and D.L. Thoe.Introduction to Partial Differential Equations with Applications.Dover, New York, 1986.