三角剖分表示法
二维和三维域
三角剖分通常用于表示计算机图形、物理建模、地理信息系统、医学成像及其他应用领域中的二维和三维几何域。如下所示的地图多边形
可以通过如下所示的地图的三角剖分来表示。
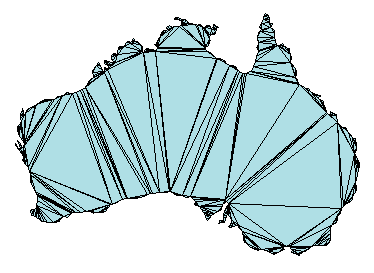
三角剖分将一个复杂的多边形分解为一组较简单的三角多边形。可以使用这些多边形开发基于几何学的算法或图形应用。
同样,可以使用三角剖分表示三维几何域的边界。下图显示了三维空间中一组点的凸包。凸包的每个分面都是三角形。
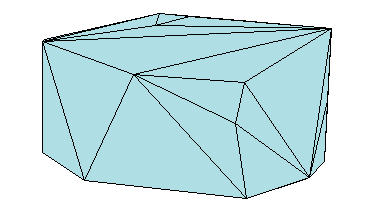
三角剖分矩阵格式
MATLAB® 使用矩阵格式表示三角剖分。此格式包含以下两个部分:
采用一个矩阵表示的顶点,该矩阵中每行包含三角剖分中一个点的坐标。
采用一个矩阵表示的三角剖分连接,该矩阵中每行定义一个三角形或四面体。
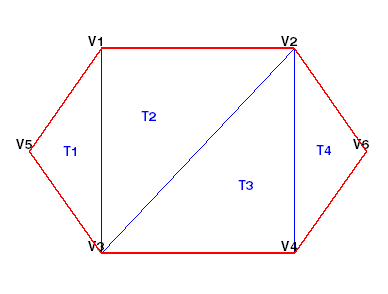
此图显示了一个简单的二维三角剖分。
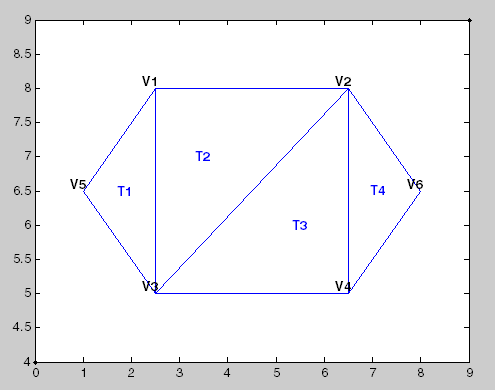
下表显示了顶点信息。
| 顶点 | ||
|---|---|---|
| 顶点 ID | x 坐标 | y 坐标 |
| V1 | 2.5 | 8.0 |
| V2 | 6.5 | 8.0 |
| V3 | 2.5 | 5.0 |
| V4 | 6.5 | 5.0 |
| V5 | 1.0 | 6.5 |
| V6 | 8.0 | 6.5 |
上一个表中的数据在 MATLAB 环境中存储为矩阵。顶点 ID 是用于标识特定顶点的标签。这些标签用于说明顶点 ID 的概念,但不会显式存储。矩阵的行号充当顶点 ID。
该表中显示了三角剖分连接数据。
| 连接 | |||
|---|---|---|---|
| 三角形 ID | 边界顶点的 ID | ||
| T1 | 5 | 3 | 1 |
| T2 | 3 | 2 | 1 |
| T3 | 3 | 4 | 2 |
| T4 | 4 | 6 | 2 |
此表中的数据在 MATLAB 环境中存储为矩阵。三角形 ID 是用于标识特定三角形的标签。这些标签用于说明三角形 ID 的概念,但不会显式存储。矩阵的行号充当三角形 ID。
可以看到三角形 T1 是由三个顶点 {V5, V3, V1} 定义的。同样,T4 是由顶点 {V4, V6, V2} 定义的。此格式可自然扩展到要求更多数据列的更高维度。例如,三维空间中的四面体由四个顶点定义,每个顶点都包含三个坐标 (x, y, z)。
您可以使用 MATLAB 来表示和查询以下类型的三角剖分:
二维三角剖分,包含由顶点和边线限定的三角形
三维曲面三角剖分,包含由顶点和边线限定的三角形
三维三角剖分,包含由顶点、边线和面限定的四面体
使用三角剖分类查询三角剖分
矩阵格式提供基于紧凑型低级别数组的表示的三角剖分。使用三角剖分开发算法时,可能需要更多有关几何属性、拓扑和邻接信息的信息。
例如,在绘制如下所示的带注解的三角剖分之前,可以计算三角形内心。在这种情况下,使用内心显示每个三角形中的三角形标签(T1、T2 等)。如果要用红色绘制边界,需要确定仅由一个三角形引用的边线。
三角剖分类
可以使用 triangulation 创建矩阵格式的任何二维或三维三角剖分数据的内存表示,例如 delaunay 函数或其他软件工具的矩阵输出。使用 triangulation 表示数据时,可以执行拓扑和几何查询,使用这些查询可开发几何算法。例如,您可以查找连接到某一顶点或共享某一条边的三角形或四面体,查找它们的外心,或查找其他特征。
可以通过以下两种方式之一创建 triangulation:
将矩阵格式的现有数据传递到
triangulation。这些数据可以是 MATLAB 函数的输出,例如delaunay或convhull。您可以导入通过其他软件应用程序创建的三角剖分数据。使用导入的数据时,请确保连接数据使用从 1 开始而不是从 0 开始的索引来引用顶点数组。将一组点传递到
delaunayTriangulation。生成的德劳内三角剖分一种特殊的triangulation。这意味着可以对数据执行任何triangulation查询以及任何德劳内特定的查询。在比较正式的 MATLAB 语言术语中,delaunayTriangulation是triangulation的子类。
通过矩阵数据创建三角剖分
此示例说明如何使用三角剖分矩阵数据创建 triangulation,探索数据,以及可以对数据执行的操作。
创建包含顶点数据的矩阵 P。
P = [ 2.5 8.0
6.5 8.0
2.5 5.0
6.5 5.0
1.0 6.5
8.0 6.5];定义连接 T。
T = [5 3 1;
3 2 1;
3 4 2;
4 6 2];从该数据创建 triangulation。
TR = triangulation(T,P)
TR =
triangulation with properties:
Points: [6×2 double]
ConnectivityList: [4×3 double]
按照访问 struct 的字段的相同方式访问 triangulation 中的属性。例如,检查包含顶点坐标的 Points 属性。
TR.Points
ans = 6×2
2.5000 8.0000
6.5000 8.0000
2.5000 5.0000
6.5000 5.0000
1.0000 6.5000
8.0000 6.5000
接下来检查连接。
TR.ConnectivityList
ans = 4×3
5 3 1
3 2 1
3 4 2
4 6 2
Points 和 ConnectivityList 属性定义三角剖分的矩阵数据。
triangulation 类是矩阵数据的包装器。真实益处是 triangulation 类方法的有用性。这些方法类似于接受 triangulation 和其他相关输入数据的函数。
triangulation 类提供了一种简单方法创建 ConnectivityList 属性矩阵的索引。访问三角剖分中的第一个三角形。
TR.ConnectivityList(1,:)
ans = 1×3
5 3 1
获取第一个三角形的另一种方法是 TR(1,:)。
检查第一个三角形的第一个顶点。
TR(1,1)
ans = 5
检查第一个三角形的第二个顶点。
TR(1,2)
ans = 3
现在检查三角剖分中的所有三角形。
TR(:,:)
ans = 4×3
5 3 1
3 2 1
3 4 2
4 6 2
使用 triplot 绘制 triangulation。triplot 函数不是 triangulation 方法,但它接受并可绘制 triangulation。
figure
triplot(TR)
axis equal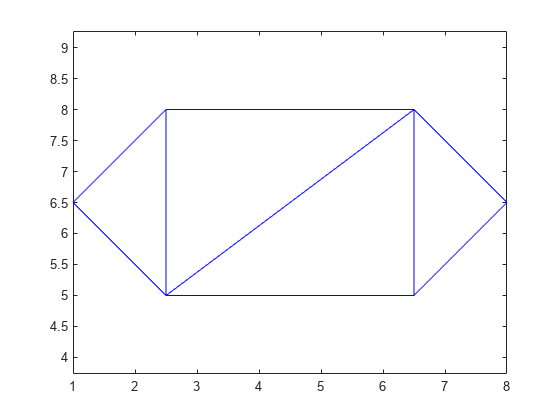
使用 triangulation 方法 freeBoundary 可查询自由边界并在绘图中突出显示该边界。该方法返回仅一个三角形共享的三角剖分边线。返回的边线以顶点 ID 方式表示。
boundaryedges = freeBoundary(TR)';
现在用红色线绘制边界线。
hold on plot(P(boundaryedges,1),P(boundaryedges,2),'-r','LineWidth',2) hold off
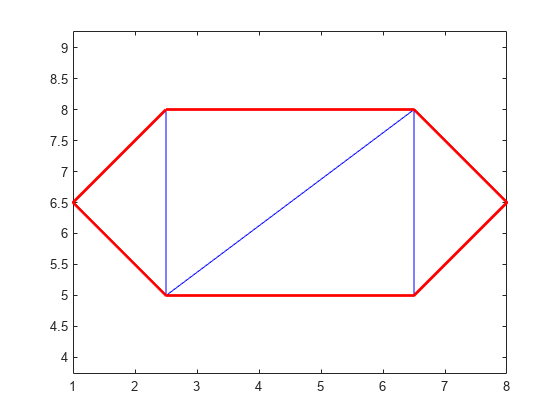
可以使用 freeBoundary 方法验证三角剖分。例如,如果观察三角剖分内部的红色边线,会发现它指明三角形的连接方式存在问题。
使用 delaunayTriangulation 创建三角剖分
此示例说明如何使用 delaunayTriangulation 创建德劳内三角剖分。
使用 delaunayTriangulation 类创建德劳内三角剖分时,会自动获得 triangulation 方法的访问权限,因为 delaunayTriangulation 是 triangulation 的子类。
基于一组点创建 delaunayTriangulation。
P = [ 2.5 8.0
6.5 8.0
2.5 5.0
6.5 5.0
1.0 6.5
8.0 6.5];
DT = delaunayTriangulation(P)DT =
delaunayTriangulation with properties:
Points: [6×2 double]
ConnectivityList: [4×3 double]
Constraints: []
生成的 delaunayTriangulation 对象具有属性 Points 和 ConnectivityList,就像 triangulation 对象一样。
使用直接索引访问三角剖分,就像 triangulation 一样。例如,可以检查第一个三角形的连接。
DT(1,:)
ans = 1×3
5 3 1
接下来,检查整个三角剖分的连接。
DT(:,:)
ans = 4×3
5 3 1
3 4 1
1 4 2
2 4 6
使用 triplot 函数绘制三角剖分。
triplot(DT)
axis equal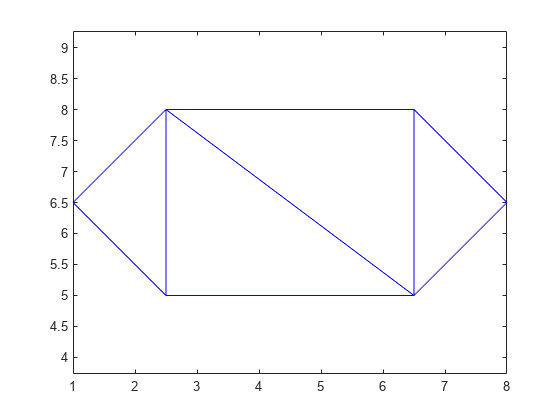
父类 triangulation 提供了 incenter 方法计算每个三角形的内心。
IC = incenter(DT)
IC = 4×2
1.8787 6.5000
3.5000 6.0000
5.5000 7.0000
7.1213 6.5000
返回的值 IC 是表示三角形内心的坐标数组。
现在,使用内心找到将三角形标签放置于绘图中的位置。
hold on numtri = size(DT,1); trilabels = arrayfun(@(P) {sprintf('T%d', P)}, (1:numtri)'); Htl = text(IC(:,1),IC(:,2),trilabels,'FontWeight','bold', ... 'HorizontalAlignment','center','Color','blue'); hold off
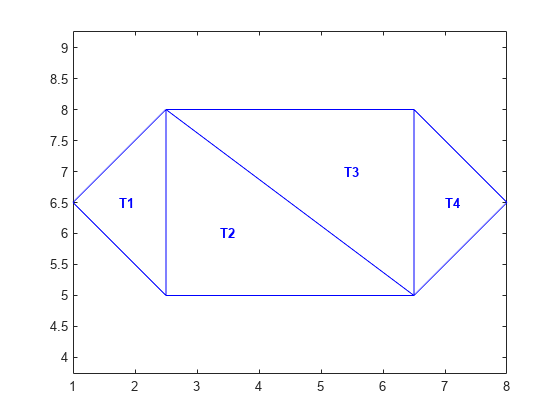
无需使用 delaunayTriangulation 创建德劳内三角剖分,可以使用 delaunay 函数创建三角剖分连接数据,然后将连接数据传递到 triangulation。例如,
P = [ 2.5 8.0
6.5 8.0
2.5 5.0
6.5 5.0
1.0 6.5
8.0 6.5];
T = delaunay(P);
TR = triangulation(T,P);
IC = incenter(TR);两种方法在此示例中都有效,但如果要创建德劳内三角剖分并对其执行查询,由于以下原因应使用 delaunayTriangulation:
delaunayTriangulation类可以提供适合处理三角剖分的其他方法。例如,可以执行最近邻点和三角形内的点搜索。它允许您编辑三角剖分以添加、移动或删除点。
它允许您创建约束性的德劳内三角剖分。这允许您创建二维域的三角剖分。
另请参阅
delaunay | delaunayTriangulation | freeBoundary | triangulation | triplot