使用德劳内三角剖分
德劳内三角剖分的定义
德劳内三角剖分广泛应用于许多不同应用程序中的科学计算。虽然有大量的计算三角剖分的算法,但德劳内三角剖分以其实用的几何属性广受欢迎。
基本属性是德劳内规则。如果是二维三角剖分,通常将其称为空外接圆规则。对于一组二维点而言,这些点的德劳内三角剖分可确保与每个三角形相关的外接圆的内部都不包含其他点。此属性非常重要。在下面的插图中,与 T1 关联的外接圆是空的。该外接圆的内部不包含任何点。与 T2 相关的外接圆为空。该外接圆的内部不包含任何点。这种三角剖分便是德劳内三角剖分。

下面的三角形则不同。与 T1 关联的外接圆不为空。它的内部包含 V3。与 T2 关联的外接圆不为空。它的内部包含 V1。这种三角剖分不是德劳内三角剖分。
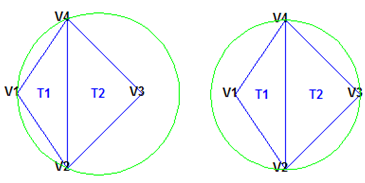
德劳内三角剖分堪称“外形整齐”,原因在于为满足空外接圆属性,优先选择带有较大内角的三角形,而不是带有较小内角的三角形。非德劳内三角剖分中的三角形在顶点 V2 和 V4 处呈锐角。如果将 {V2, V4} 边替换为连接 V1 和 V3 的边,会实现最小角的最大化并且使得该三角剖分变为德劳内三角剖分。另外,德劳内三角剖分将最近邻点的点连接在一起。这两个特征(外形整齐和最近邻点关系)在实践中具有重要的作用,有助于促进在散点数据插值中使用德劳内三角剖分。
虽然德劳内属性定义明确,但存在退化点集时三角剖分的拓扑并不唯一。在二维中,4 个或更多特征点位于同一圆中时会引发退化。例如,正方形的顶点不具有唯一的德劳内三角剖分。

德劳内三角剖分的属性扩展到更高的维度。三维点集的三角剖分由四面体组成。下图显示了一个简单的由 2 个四面体组成的三维德劳内三角剖分。显示一个四面体的外接球以突出显示空外接球规则。
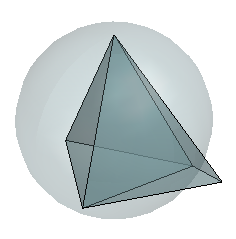
三维德劳内三角剖分可生成符合空外接球规则的四面体。
创建德劳内三角剖分
MATLAB® 提供两种创建德劳内三角剖分的方法:
函数
delaunay和delaunayn
delaunay 函数支持创建二维和三维德劳内三角剖分。delaunayn 函数支持创建四维或更高维度的德劳内三角剖分。
提示
对于中型至大型点集而言,由于所需的内存呈指数级增长,创建六维以上的德劳内三角剖分通常不太现实。
delaunayTriangulation 类支持创建二维和三维德劳内三角剖分。它提供了多种适用于开发基于三角剖分的算法的方法。这些类方法与函数相似,但它们仅限于处理使用 delaunayTriangulation 创建的三角剖分。delaunayTriangulation 类还支持创建相关构造,例如凸包和沃罗诺伊图。它还支持创建约束性德劳内三角剖分。
总的说来:
在仅需要基本三角剖分数据并且数据对应用程序已足够完整时,
delaunay函数非常有用。delaunayTriangulation类提供了更多功能用于开发基于三角剖分的应用程序。在需要三角剖分并且希望执行以下任意操作时,该类非常有用:在三角剖分中搜索包含查询点的三角形或四面体。
使用三角剖分执行最近邻点搜索。
查询三角剖分的拓扑邻接或几何属性。
修改三角剖分以插入或删除点。
约束三角剖分中的边界 - 这称为约束性的德劳内三角剖分。
对多边形进行三角剖分并(可选)删除域外部的三角形。
使用德劳内三角剖分计算凸包或沃罗诺伊图。
使用德劳内和 delaunayn 函数
delaunay 和 delaunayn 函数获取点集并生成矩阵格式的三角剖分。请参阅三角剖分矩阵格式以了解有关该数据结构体的详细信息。在二维模式下,delaunay 函数通常用于生成此类三角剖分,即它可用于绘制根据一组分散数据点来定义的曲面。在该应用中,必须注意该方法仅在曲面为单值型时可用。例如,它不能用于绘制球面,因为有两个 z 值对应于同一个 (x, y) 坐标。通过一个简单示例来演示 delaunay 函数如何可用于绘制表示抽样数据集的曲面。
MATLAB 提供 delaunayn 函数以支持创建四维及更高维的德劳内三角剖分。此外,还提供了两个补充函数 tsearchn 和 dsearchn,以支持对 N 维三角剖分执行空间搜索。有关基于三角剖分的搜索的详细信息,请参阅空间搜索。
创建二维德劳内三角剖分
此示例说明如何使用 delaunay 函数创建海底山数据集的二维德劳内三角剖分。海底山是指水下山脉。该数据集包含一组经度 (x) 和纬度 (y) 位置,以及在这些坐标测量的对应海底山海拔 (z)。
加载海底山数据集并以散点图的方式查看 (x, y) 数据。
load seamount plot(x,y,".",MarkerSize=12) xlabel("Longitude") ylabel("Latitude") grid on

从该点集构建德劳内三角剖分,并使用 triplot 在现有图窗中绘制三角剖分。
tri = delaunay(x,y); hold on triplot(tri,x,y) hold off
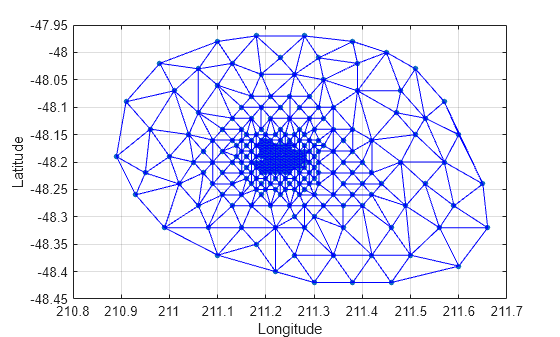
添加海底山的深度数据 (z) 以提高顶点并创建曲面。创建新图窗并在线框模式下使用 trimesh 绘制曲面。
figure hidden on trimesh(tri,x,y,z) xlabel("Longitude") ylabel("Latitude") zlabel("Depth in Feet")

如果想要在着色模式下绘制该曲面,请使用 trisurf 而不是 trimesh。
也可以使用 delaunay 函数来创建三维德劳内三角剖分。此三角剖分由四面体构成。
创建三维德劳内三角剖分
此示例说明如何创建随机数据集的三维德劳内三角剖分。该三角剖分使用 tetramesh 进行绘图,FaceAlpha 选项增加了绘图的透明度。
rng('default') X = rand([30 3]); tet = delaunay(X); faceColor = [0.6875 0.8750 0.8984]; tetramesh(tet,X,'FaceColor',faceColor,'FaceAlpha',0.3)

使用 delaunayTriangulation 类
delaunayTriangulation 类提供另一种在 MATLAB 中创建德劳内三角剖分的方法。虽然 delaunay 和 delaunayTriangulation 使用相同的基本算法并生成相同的三角剖分,但 delaunayTriangulation 提供了适用于开发基于德劳内的算法的补充方法。这些方法与函数类似,可以将它们与三角剖分数据一起打包到称为类的容器中。将所有内容集中在类中,这样可以提供更加有条理的结构,从而提高易用性。它还可以提高基于三角剖分的搜索的性能,例如点位置和最近邻位置。delaunayTriangulation 支持对德劳内三角剖分进行增量编辑。还可以实行二维中的边约束。
三角剖分表示法引入了 triangulation 类,该类支持对二维和三维三角剖分进行拓扑和几何查询。delaunayTriangulation 是一种特殊的 triangulation。这意味着除了可以对 delaunayTriangulation 执行德劳内特定的查询外,还可以执行任何 triangulation 查询。在比较正式的 MATLAB 语言术语中,delaunayTriangulation 是 triangulation 的子类。
创建、查询和编辑德劳内三角剖分
此示例说明如何使用 delaunayTriangulation 创建、查询和编辑 seamount 数据的德劳内三角剖分。海底山数据集包含用于定义海拔山曲面的 (x, y) 位置和对应的海拔 (z)。
加载 (x, y) 数据并进行三角剖分。
load seamount
DT = delaunayTriangulation(x,y)DT =
delaunayTriangulation with properties:
Points: [294×2 double]
ConnectivityList: [566×3 double]
Constraints: []
由于没有施加任何边约束,因此 Constraints 属性为空。Points 属性表示顶点坐标,ConnectivityList 属性表示三角形。这两个属性共同定义了三角剖分的矩阵数据。
delaunayTriangulation 类是矩阵数据的包装器,并且提供了一组补充方法。可以按照访问结构体字段的方式访问 delaunayTriangulation 中的属性。
访问顶点数据。
DT.Points;
访问连接数据。
DT.ConnectivityList;
访问 ConnectivityList 属性中的第一个三角形。
DT.ConnectivityList(1,:)
ans = 1×3
230 205 152
delaunayTriangulation 提供了一种对 ConnectivityList 属性矩阵进行索引的简单方法。
访问第一个三角形。
DT(1,:)
ans = 1×3
230 205 152
检查第一个三角形的第一个顶点。
DT(1,1)
ans = 230
检查三角剖分中的所有三角形。
DT(:,:);
对 delaunayTriangulation 输出 DT 进行索引,这与对 delaunay 的三角剖分数组输出进行索引类似。二者的区别是您可以对 DT 调用额外方法(例如 nearestNeighbor 和 pointLocation)。
使用 triplot 绘制 delaunayTriangulation。triplot 函数不是 delaunayTriangulation 方法,但它接受并可绘制 delaunayTriangulation。
triplot(DT) axis equal xlabel("Longitude") ylabel("Latitude") grid on
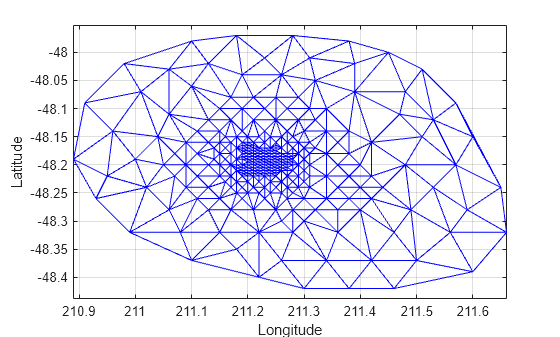
或者,可以使用 triplot(DT(:,:), DT.Points(:,1), DT.Points(:,2)); 获取相同的绘图。
使用 delaunayTriangulation 方法 convexHull 计算凸包并将其添加到绘图。由于您已经有一个德劳内三角剖分,因此可利用此方法来获得凸包,效率比使用 convhull 的完全计算方法更高。
hold on k = convexHull(DT); xHull = DT.Points(k,1); yHull = DT.Points(k,2); plot(xHull,yHull,"r",LineWidth=2) hold off
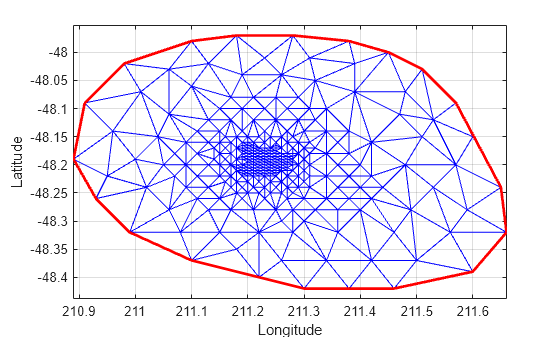
您可以按增量方式编辑 delaunayTriangulation,以添加或删除点。如果需要将点添加到现有的三角剖分,增量添加方法的速度要快于对增广点集进行完整的重新三角剖分。当要删除的点数量相对现有的点数量较小时,增量点删除的效率更高。
编辑三角剖分,删除上一次计算的凸包上的点。
figure plot(xHull,yHull,"r",LineWidth=2) axis equal xlabel("Longitude") ylabel("Latitude") grid on % The convex hull topology duplicates the start and end vertex. % Remove the duplicate entry. k(end) = []; % Now remove the points on the convex hull. DT.Points(k,:) = []
DT =
delaunayTriangulation with properties:
Points: [274×2 double]
ConnectivityList: [528×3 double]
Constraints: []
% Plot the new triangulation. hold on triplot(DT) hold off
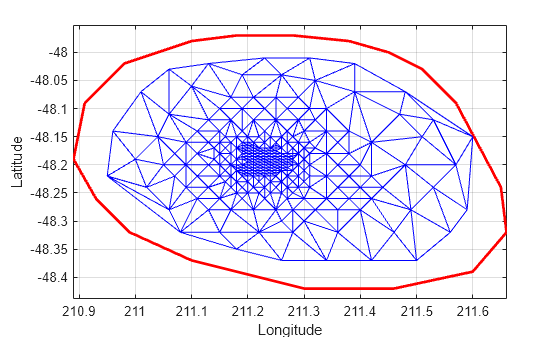
紧靠凸包边界内侧有一个未删除的顶点。在图窗中使用放大工具可以看到,它确实处于凸包以内。您可以绘制顶点标签,以确定此顶点的索引,并从三角剖分中将其删除。或者,可以使用 nearestNeighbor 方法更轻松地确定索引。
该点靠近位置 (211.6, -48.15)。使用 nearestNeighbor 方法求最近的顶点。
vertexId = nearestNeighbor(DT,211.6,-48.15)
vertexId = 50
现在从三角剖分中删除该顶点。
DT.Points(vertexId,:) = []
DT =
delaunayTriangulation with properties:
Points: [273×2 double]
ConnectivityList: [525×3 double]
Constraints: []
对新的三角剖分进行绘图。
figure plot(xHull,yHull,"r",LineWidth=2) axis equal xlabel("Longitude") ylabel("Latitude") grid on hold on triplot(DT) hold off
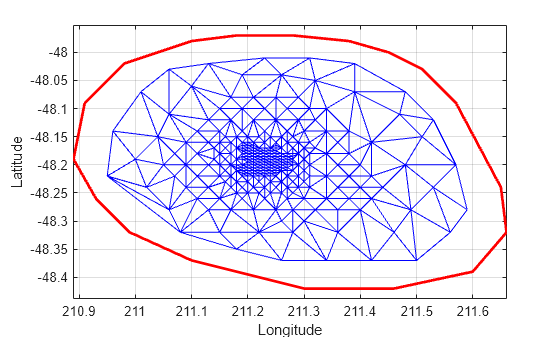
将点添加到现有的三角剖分。添加 4 个点,在三角剖分的周围构成一个矩形。
Padditional = [210.9 -48.5; 211.6 -48.5; ...
211.6 -47.9; 210.9 -47.9];
DT.Points(end+(1:4),:) = PadditionalDT =
delaunayTriangulation with properties:
Points: [277×2 double]
ConnectivityList: [548×3 double]
Constraints: []
关闭所有现有图窗。
close all对新的三角剖分进行绘图。
figure plot(xHull,yHull,"r",LineWidth=2) axis equal xlabel("Longitude") ylabel("Latitude") grid on hold on triplot(DT) hold off
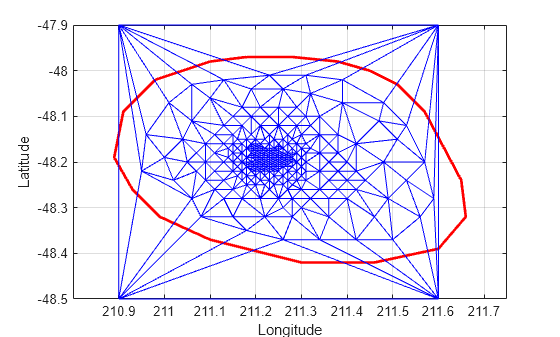
您可以编辑三角剖分中的点,将其移到新位置。编辑附加点集的第一个点(顶点 ID 274)。
DT.Points(274,:) = [211 -48.4];
关闭所有现有图窗。
close all对新的三角剖分进行绘图
figure plot(xHull,yHull,"r",LineWidth=2) axis equal xlabel("Longitude") ylabel("Latitude") grid on hold on triplot(DT) hold off
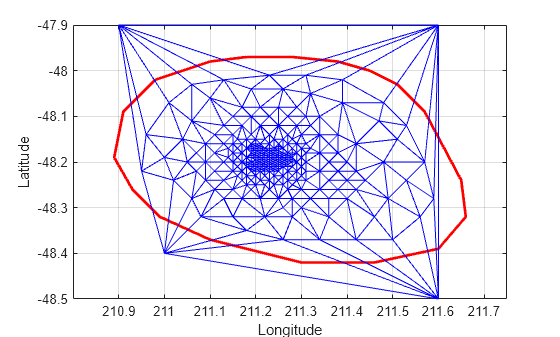
使用 triangulation 类的方法 vertexAttachments 求连接的三角形。由于连接到顶点的三角形数量是可变的,因此该方法将在元胞数组中返回连接的三角形 ID。您需要使用括号提取内容。
attTris = vertexAttachments(DT,274); hold on triplot(DT(attTris{:},:),DT.Points(:,1),DT.Points(:,2),'g') hold off
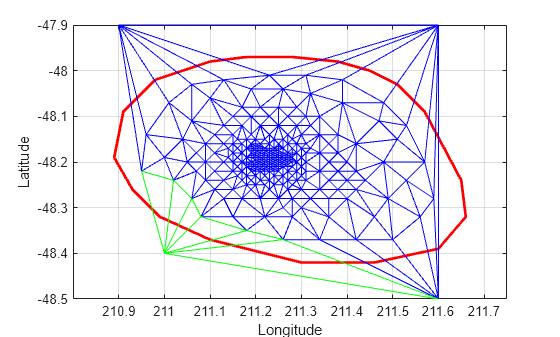
delaunayTriangulation 也可以用于对三维空间中的点进行三角剖分。生成的三角剖分由四面体构成。
创建并绘制三维点的德劳内三角剖分
此示例说明如何使用 delaunayTriangulation 创建并绘制三维点的三角剖分。
rng("default")
P = rand(30,3);
DT = delaunayTriangulation(P)DT =
delaunayTriangulation with properties:
Points: [30×3 double]
ConnectivityList: [102×4 double]
Constraints: []
faceColor = [0.6875 0.8750 0.8984]; tetramesh(DT,FaceColor=faceColor,FaceAlpha=0.3)

tetramesh 函数会同时绘制三角剖分的内面和外面。对于大型三维三角剖分,绘制内面可能导致不必要的资源使用。绘制边界可能更加适宜。您可以使用 freeBoundary 方法获取矩阵格式的边界三角剖分。然后将结果传递给 trimesh 或 trisurf。
受约束的德劳内三角剖分
delaunayTriangulation 类允许您约束二维三角剖分中的边界。这意味着可以选择三角剖分中的一对点并约束用于连接这些点的边。可以将其作为“施加压力”绘制一对或多对点之间的边界。以下示例说明了边约束对三角剖分的影响。
下面的三角剖分是德劳内三角剖分,因为它符合空外接圆规则。

受约束的德劳内三角剖分
使用指定的顶点 V1 和 V3 间的边约束对点集进行三角剖分。
定义点集。
P = [2 4; 6 1; 9 4; 6 7];
定义 V1 与 V3 之间的约束 C。
C = [1 3]; DT = delaunayTriangulation(P,C);
对三角剖分绘图并添加注解。
triplot(DT) % Label the vertices. hold on numvx = size(P,1); vxlabels = arrayfun(@(n) {sprintf("V%d", n)},(1:numvx)'); Hpl = text(P(:,1)+0.2, P(:,2)+0.2, vxlabels, FontWeight="bold", ... HorizontalAlignment="center", BackgroundColor="none"); hold off % Use the incenters to find the positions for placing triangle labels on the plot. hold on IC = incenter(DT); numtri = size(DT,1); trilabels = arrayfun(@(P) {sprintf('T%d', P)},(1:numtri)'); Htl = text(IC(:,1),IC(:,2),trilabels,FontWeight="bold", ... HorizontalAlignment="center",Color="blue"); hold off % Plot the circumcircle associated with the triangle, T1. hold on [CC,r] = circumcenter(DT); theta = 0:pi/50:2*pi; xunit = r(1)*cos(theta) + CC(1,1); yunit = r(1)*sin(theta) + CC(1,2); plot(xunit,yunit,"g") axis equal hold off

已遵循顶点(V1、V3)之间的约束,但导致德劳内规则失效。此外还导致德劳内三角剖分固有的最近邻关系失效。这意味着如果三角剖分包含约束,则无法支持 delaunayTriangulation 提供的 nearestNeighbor 搜索方法。
在典型应用中,三角剖分可能由大量点构成,并且三角剖分中受到约束的边可能相对较少。此类三角剖分被视为局部非德劳内三角剖分,因为三角剖分中的许多三角形可能遵循德劳内规则,但在局部可能存在一些不遵循该规则的三角形。在许多应用中,空外接圆属性的局部松弛不成问题。
受约束的三角剖分通常用于对非凸多边形进行三角剖分。这些约束在多边形边与三角剖分边间建立了对应关系。利用此关系,可以提取表示该区域的三角剖分。以下示例说明如何使用受约束的 delaunayTriangulation 对非凸多边形进行三角剖分。
定义并绘制多边形。
figure() axis([-1 17 -1 6]); axis equal P = [0 0; 16 0; 16 2; 2 2; 2 3; 8 3; 8 5; 0 5]; patch(P(:,1),P(:,2),'-r',LineWidth=2,FaceColor="none",EdgeColor="r"); % Label the points. hold on numvx = size(P,1); vxlabels = arrayfun(@(n) {sprintf("P%d", n)},(1:numvx)'); Hpl = text(P(:,1)+0.2, P(:,2)+0.2, vxlabels,FontWeight="bold", ... HorizontalAlignment="center",BackgroundColor="none"); hold off

创建并绘制三角剖分以及多边形边界。
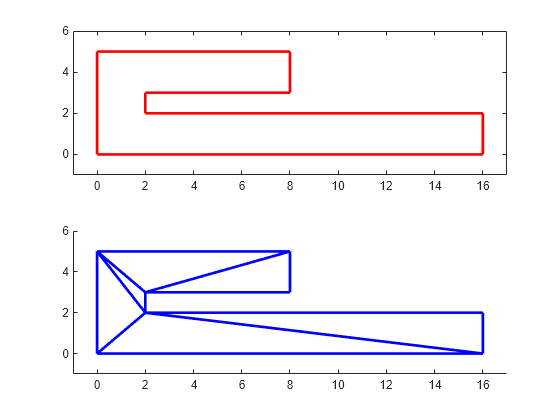
figure() subplot(2,1,1); axis([-1 17 -1 6]); axis equal P = [0 0; 16 0; 16 2; 2 2; 2 3; 8 3; 8 5; 0 5]; DT = delaunayTriangulation(P); triplot(DT) hold on patch(P(:,1),P(:,2),'-r',LineWidth=2,FaceColor="none",EdgeColor="r"); hold off % Plot the standalone triangulation in a subplot. subplot(2,1,2); axis([-1 17 -1 6]); axis equal triplot(DT)
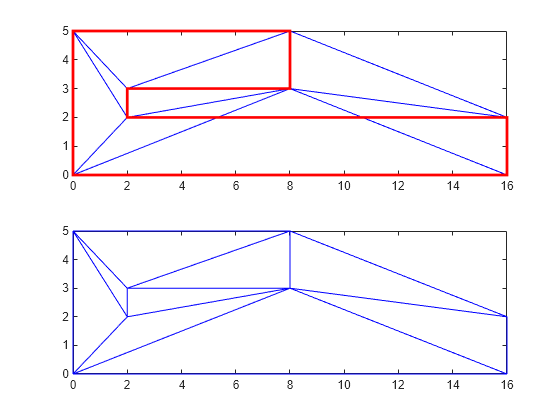
此三角剖分不能用于表示多边形域,因为一些三角形横跨了边界。您需要对被三角剖分边切割的边施加约束。由于必须符合所有边的要求,因此需要约束所有边。以下步骤说明如何约束所有边。
输入约束边定义。观察需要约束((V1, V2) 间、(V2, V3) 间,以此类推)的带注解的图窗。
C = [1 2; 2 3; 3 4; 4 5; 5 6; 6 7; 7 8; 8 1];
一般而言,如果在定义多边形边界的序列中有 N 个点,则可以将约束表示为 C = [(1:(N-1))' (2:N)'; N 1];。
在创建 delaunayTriangulation 时指定约束。
DT = delaunayTriangulation(P,C);
也可以通过设置 Constraints 属性:DT.Constraints = C;,来对现有的三角剖分施加约束。
绘制三角剖分和多边形。
figure(Color="white") subplot(2,1,1); axis([-1 17 -1 6]); axis equal triplot(DT) hold on patch(P(:,1),P(:,2),'-r',LineWidth=2,FaceColor="none",EdgeColor="r"); hold off % Plot the standalone triangulation in a subplot. subplot(2,1,2); axis([-1 17 -1 6]); axis equal triplot(DT)
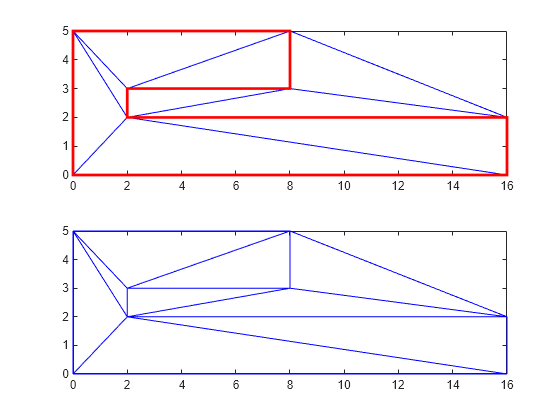
该绘图显示,三角剖分的边符合多边形边界要求。但三角剖分会填充凹处。这种情况下需要一个表示多边形域的三角剖分。您可以使用 delaunayTriangulation 方法 isInterior 从多边形内提取三角形。此方法会返回一个逻辑数组,其 true 值和 false 值指示三角形是否在有界的几何域内。该分析基于约当曲线定理,并且通过边约束定义边界。如果第 i 个逻辑标志为 true,则三角剖分中的第 i 个三角形被视为在域内,否则被视为在域外。
现在使用 isInterior 方法来计算并绘制域中的一系列三角形。
% Plot the constrained edges in red. figure(Color="white") subplot(2,1,1); plot(P(C'),P(C'+size(P,1)),"-r",LineWidth=2); axis([-1 17 -1 6]); % Compute the in/out status. IO = isInterior(DT); subplot(2,1,2); hold on axis([-1 17 -1 6]); % Use triplot to plot the triangles that are inside. % Uses logical indexing and dt(i,j) shorthand % format to access the triangulation. triplot(DT(IO, :),DT.Points(:,1),DT.Points(:,2),LineWidth=2) hold off
包含重复位置的点集的三角剖分
MATLAB 中的德劳内算法可以基于特征点集构建三角剖分。如果传递到三角剖分函数或类的点不是特征点,会检测到重复位置并忽略重复点。这样生成的三角剖分不会参照原始输入中的一些点,即重复点。使用 delaunay 和 delaunayn 函数时,重复情况的存在可能没什么影响。但是,由于 delaunayTriangulation 类提供的许多查询以索引为基础,因此必须了解 delaunayTriangulation 对特征数据集执行三角剖分和处理。因此,基于唯一点集创建索引是惯例。这些数据通过 delaunayTriangulation 的 Points 属性维护。
以下示例说明了在处理 delaunayTriangulation 时参照在 Points 属性内存储的特征数据集的重要性:
rng('default')
P = rand([25 2]);
P(18,:) = P(8,:)
P(16,:) = P(6,:)
P(12,:) = P(2,:)
DT = delaunayTriangulation(P)
Points 属性显示已从数据中删除重复点。DT =
delaunayTriangulation with properties:
Points: [22x2 double]
ConnectivityList: [31x3 double]
Constraints: []DT.Points 的索引。因此,使用以下代码计算并绘制凸包:K = DT.convexHull(); plot(DT.Points(:,1),DT.Points(:,2),'.'); hold on plot(DT.Points(K,1),DT.Points(K,2),'-r');
delaunayTriangulation 提供的索引一起使用,则结果不正确。delaunayTriangulation 处理基于特征数据集 DT.Points 的索引。例如,以下内容会生成错误的绘图,因为 K 的索引是关于 DT.Points 的,而不是关于 P 的。K = DT.convexHull(); plot(P(:,1),P(:,2),'.'); hold on plot(P(K,1),P(K,2),'-r');
delaunayTriangulation 之前删除重复项来创建特征数据集,通常更为方便。这样做将消除可能会出现混淆的情况。如下所示,可以使用 unique 函数完成上述操作: rng('default') P = rand([25 2]); P(18,:) = P(8,:) P(16,:) = P(6,:) P(12,:) = P(2,:) [~, I, ~] = unique(P,'first','rows'); I = sort(I); P = P(I,:); DT = delaunayTriangulation(P) % The point set is unique