Main Content

空间搜索

打开实时脚本

简介

MATLAB® 提供了使用德劳内三角剖分或常规三角剖分执行空间搜索所必需的函数。MATLAB 支持的搜索查询包括：

  • 最近邻点搜索（有时称为最近点搜索或邻近搜索）。

  • 点位置搜索（有时称为三角形内的点搜索或单纯形内的点搜索，其中单纯形是三角形、四面体或更高维度的等效形状）。

如果是欧几里德空间中的点集 X 和查询点 q，最近邻点搜索将查找 X 中比 X 中的任何其他点都邻近 q 的点 p。如果是 X 的三角剖分，点位置搜索将查找包含查询点 q 的三角形或四面体。由于这些方法适用于德劳内三角剖分以及常规三角剖分，因此即使对点的修改违反了德劳内准则，也可以使用它们。您也可以搜索表示为矩阵格式的常规三角剖分。

尽管 MATLAB 支持在 N 维中执行这些搜索方案，但维数在三维以上时通常禁止使用精确的空间搜索。应考虑使用近似的替代方法来解决多达 10 维时的大型问题。

最近邻点搜索

根据问题的维度，MATLAB 中有多种方法可计算最近邻点：

  • 对于二维和三维搜索，使用 triangulation 类提供并由 delaunayTriangulation 类继承的 nearestNeighbor 方法。

  • 对于 4 维和更高维，使用 delaunayn 函数构建三角剖分，并使用补充的 dsearchn 函数执行搜索。虽然这些 N 维函数支持二维和三维，但它们并没有三角剖分提供的搜索方法通用和高效。

此示例说明如何使用 delaunayTriangulation 执行二维最近邻搜索。

首先创建一个包含 15 个点的随机点集。

X = [3.5 8.2; 6.8 8.3; 1.3 6.5; 3.5 6.3; 5.8 6.2; 8.3 6.5;...
    1 4; 2.7 4.3; 5 4.5; 7 3.5; 8.7 4.2; 1.5 2.1; 4.1 1.1; ...
    7 1.5; 8.5 2.75];

绘制这些点并添加注释，以显示 ID 标签。

plot(X(:,1),X(:,2),'ob')
hold on
vxlabels = arrayfun(@(n) {sprintf('X%d', n)}, (1:15)');
Hpl = text(X(:,1)+0.2, X(:,2)+0.2, vxlabels, 'FontWeight', ...
    'bold', 'HorizontalAlignment','center', 'BackgroundColor', ...
    'none');
hold off

创建这些点的德劳内三角剖分。

dt = delaunayTriangulation(X);

创建一些查询点，并使用 nearestNeighbor 方法针对每个查询点在 X 中查找其对应的最近邻的索引。

numq = 10;
rng(0,'twister');
q = 2+rand(numq,2)*6;
xi = nearestNeighbor(dt, q);

在绘图中添加查询点，并添加将查询点连接到其最近邻的线段。

xnn = X(xi,:);

hold on
plot(q(:,1),q(:,2),'or');
plot([xnn(:,1) q(:,1)]',[xnn(:,2) q(:,2)]','-r');

vxlabels = arrayfun(@(n) {sprintf('q%d', n)}, (1:numq)');
Hpl = text(q(:,1)+0.2, q(:,2)+0.2, vxlabels, 'FontWeight', ...
    'bold', 'HorizontalAlignment','center', ...
    'BackgroundColor','none');

hold off

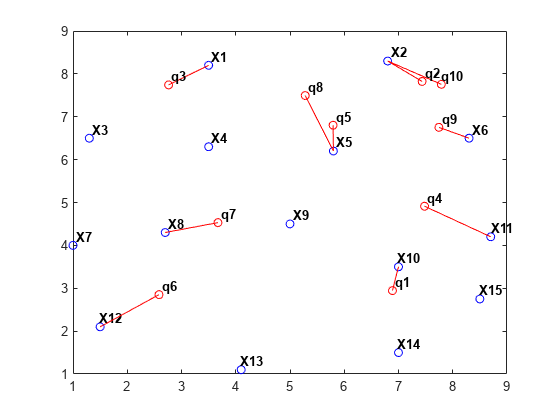
执行三维最近邻搜索是对基于 delaunayTriangulation 的二维示例的直接扩展。

对于四维以及更高维而言，使用以下示例中所述的 delaunayn 和 dsearchn 函数：

创建四维随机样本点，并使用 delaunayn 对这些点执行三角剖分：

X = 20*rand(50,4) -10;
tri = delaunayn(X);

创建一些查询点，使用 dsearchn 函数针对每个查询点在 X 间查找与其对应的最近邻点的索引：

q = rand(5,4);
xi = dsearchn(X,tri, q);

nearestNeighbor 方法和 dsearchn 函数允许以可选参量的形式返回查询点与其最近邻点之间的欧几里德距离。在四维示例中，可以计算距离 (dnn)，如下所示：

[xi,dnn] = dsearchn(X,tri,q);

点位置搜索

点位置搜索是一种通过封闭查询点来确定单纯形（三角形、四面体等）的三角剖分搜索算法。在最近邻点搜索的情况下，根据问题的维度，在 MATLAB 中执行点位置搜索有多种方法：

  • 对二维和三维，使用基于类的方式，以及由 triangulation 类提供并由 delaunayTriangulation 类继承的 pointLocation 方法。

  • 对于 4 维和更高维，使用 delaunayn 函数构建三角剖分，并使用补充的 tsearchn 函数执行点位置搜索。虽然这些 N 维函数支持二维和三维，但它们并没有三角剖分提供的搜索方法通用和高效。

此示例说明如何使用 delaunayTriangulation 类来执行二维点位置搜索。

首先从一个二维点集开始。

X = [3.5 8.2; 6.8 8.3; 1.3 6.5; 3.5 6.3; 5.8 6.2; ...
    8.3 6.5; 1 4; 2.7 4.3; 5 4.5; 7 3.5; 8.7 4.2; ...
    1.5 2.1; 4.1 1.1; 7 1.5; 8.5 2.75];

创建并绘制三角剖分，在三角形的内心显示三角形 ID 标签。

dt = delaunayTriangulation(X);
triplot(dt);

hold on
ic = incenter(dt);
numtri = size(dt,1);
trilabels = arrayfun(@(x) {sprintf('T%d', x)}, (1:numtri)');
Htl = text(ic(:,1), ic(:,2), trilabels, 'FontWeight', ...
      'bold', 'HorizontalAlignment', 'center', 'Color', ...
      'blue');
hold off

现在创建一些查询点，并将其添加到绘图中。然后使用 pointLocation 方法查找对应的包围三角形的索引。

q = [5.9344    6.2363;
    2.2143    2.1910;
    7.0948    3.6615;
    7.6040    2.2770;
    6.0724    2.5828;
    6.5464    6.9407;
    6.4588    6.1690;
    4.3534    3.9026;
    5.9329    7.7013;
    3.0271    2.2067];

hold on; 
plot(q(:,1),q(:,2),'*r'); 
vxlabels = arrayfun(@(n) {sprintf('q%d', n)}, (1:10)');
Hpl = text(q(:,1)+0.2, q(:,2)+0.2, vxlabels, 'FontWeight', ...
    'bold', 'HorizontalAlignment','center', ... 
    'BackgroundColor', 'none');
hold off

ti = pointLocation(dt,q);

执行三维点位置搜索是对使用 delaunayTriangulation 执行二维点位置搜索的直接扩展。

对于四维以及更高维而言，使用以下示例中所述的 delaunayn 和 tsearchn 函数：

创建四维随机样本点，然后使用 delaunayn 进行三角剖分：

X = 20*rand(50,4) -10;
tri = delaunayn(X);

使用 tsearchn 函数创建一些查询点，求出对应封闭单纯形的索引：

q = rand(5,4);
ti = tsearchn(X,tri,q);

pointLocation 方法和 tsearchn 函数允许以可选参量的形式返回对应的重心坐标。在四维示例中，可按如下方式计算重心坐标：

[ti,bc] = tsearchn(X,tri,q);

重心坐标对执行线性插值很有用。这些坐标提供了可用于在封闭单纯形的每个顶点缩放数值的权值。有关详细信息，请参阅内插散点数据。

另请参阅

| | | | | | | |

相关主题