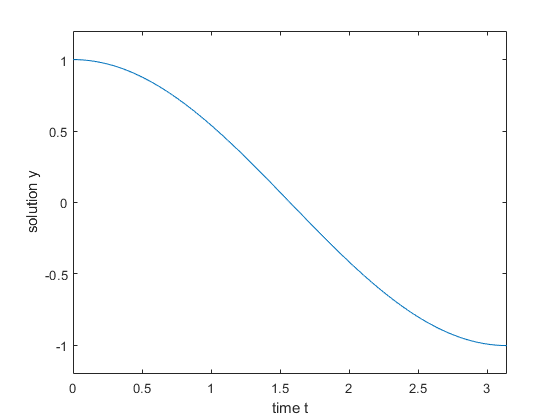
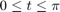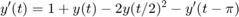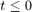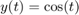ddensd
求解中立型时滞微分方程 (DDE)
语法
说明
示例
输入参数
输出参量
详细信息
算法
有关此求解器使用的算法的信息,请参阅 Shampine [2]。
参考
[1] Paul, C.A.H. “A Test Set of Functional Differential Equations.” Numerical Analysis Reports. No. 243. Manchester, UK: Math Department, University of Manchester, 1994.
[2] Shampine, L.F. “Dissipative Approximations to Neutral DDEs.” Applied Mathematics & Computation. Vol. 203, Number 2, 2008, pp. 641–648.
版本历史记录
在 R2012b 中推出