ellipj
雅可比椭圆函数
说明
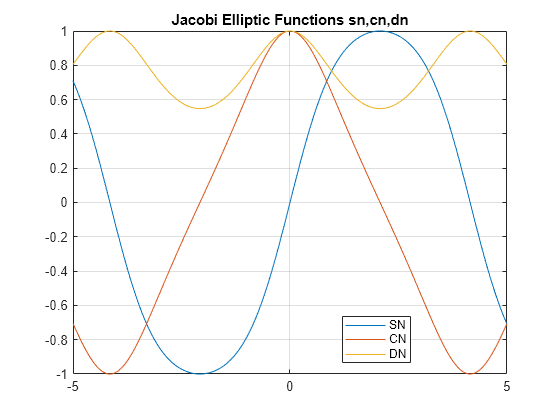
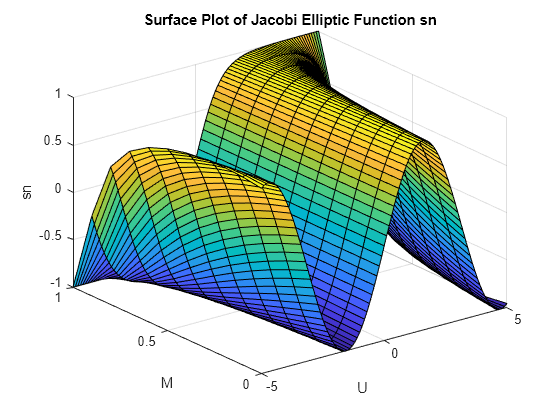
示例
输入参数
输出参量
详细信息
算法
ellipj 使用 [1] 中介绍的算术几何均值方法计算雅可比椭圆函数。首先定义三元组
ellipj 使用以下公式计算连续迭代
然后,它使用以下公式计算振幅(以弧度为单位)
请注意正确展开相位。然后,雅可比椭圆函数则可表示为
参考
[1] Abramowitz, M. and I. A. Stegun, Handbook of Mathematical Functions, Dover Publications, 1965, 17.6.
扩展功能
版本历史记录
在 R2006a 之前推出