Main Content

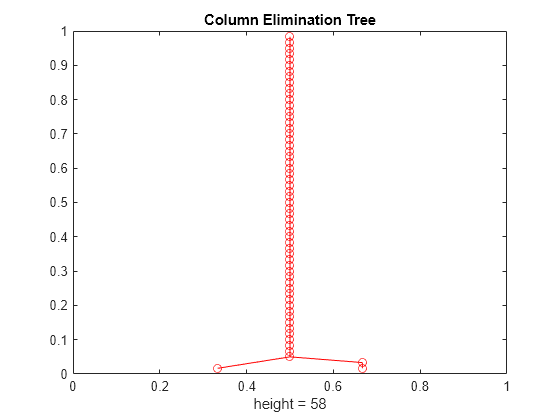
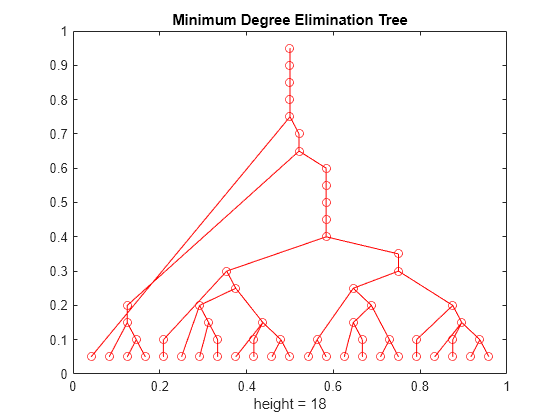
etree

消去树

全页折叠

语法

p = etree(A)
p = etree(A,type)
[p,q] = etree(___)

说明

p = etree(A) 构造与 A 具有相同上三角的对称方阵并返回该方阵的消去树。

示例

p = etree(A,type) 指定消去树的类型。例如，如果 type 是 "lo"，则 etree 使用 A 的下三角来构造对称方阵。

示例

[p,q] = etree(___) 还返回消去树的后序排列 q。您可以使用上述语法中的任意输入参量组合指定两个输出。

示例

全部折叠

打开实时脚本

创建一个由 0 和 1 组成的 7×7 三对角矩阵。

A = diag(ones(1,7)) + diag(ones(1,6),1) + diag(ones(1,6),-1)
A = 7×7

     1     1     0     0     0     0     0
     1     1     1     0     0     0     0
     0     1     1     1     0     0     0
     0     0     1     1     1     0     0
     0     0     0     1     1     1     0
     0     0     0     0     1     1     1
     0     0     0     0     0     1     1

计算 A 的消去树。消去树的每个元素 p(i) 表示节点 i 的父级。p(7) 是 0，因为节点 7 是树的根。

p = etree(A)
p = 1×7

     2     3     4     5     6     7     0

创建一个由 0 和 1 组成的 6×6 分块对角矩阵。

a = ones(3);
b = zeros(3);
B = [a b; b a]
B = 6×6

     1     1     1     0     0     0
     1     1     1     0     0     0
     1     1     1     0     0     0
     0     0     0     1     1     1
     0     0     0     1     1     1
     0     0     0     1     1     1

计算 B 的消去树。etree 返回一个包含两个消去树的林，由索引 3 和 6 处的根节点指示。

r = etree(B)
r = 1×6

     2     3     0     5     6     0
打开实时脚本

计算 bucky 稀疏矩阵的两个不同消去树。"lo" 消去树使用 A 的下三角，而 "col" 消去树使用矩阵 A'*A。

A = bucky;
p1 = etree(A,"lo");
p2 = etree(A,"col");

使用 treeplot 绘制消去树。

treeplot(p1)
title("Lower Triangle Elimination Tree")

Figure contains an axes object. The axes object with title Lower Triangle Elimination Tree, xlabel height = 58 contains 2 objects of type line. One or more of the lines displays its values using only markers

treeplot(p2)
title("Column Elimination Tree")

Figure contains an axes object. The axes object with title Column Elimination Tree, xlabel height = 58 contains 2 objects of type line. One or more of the lines displays its values using only markers

打开实时脚本

计算 bucky 稀疏矩阵的两种排列的消去树。使用 symrcm 创建对称反向卡西尔-麦基排序，使用 symamd 创建对称近似最小度排序。

A = bucky;
r = symrcm(A);
p1 = etree(A(r,r));
m = symamd(A);
p2 = etree(A(m,m));

使用 treeplot 绘制消去树。反向卡西尔-麦基消去树是一排节点，而最小度消去树有多个不相交的分支。

treeplot(p1)
title("Reverse Cuthill-McKee Elimination Tree")

Figure contains an axes object. The axes object with title Reverse Cuthill-McKee Elimination Tree, xlabel height = 59 contains 2 objects of type line. One or more of the lines displays its values using only markers

treeplot(p2)
title("Minimum Degree Elimination Tree")

Figure contains an axes object. The axes object with title Minimum Degree Elimination Tree, xlabel height = 18 contains 2 objects of type line. One or more of the lines displays its values using only markers

使用 spy 绘制稀疏模式。矩阵的消去树依赖其稀疏模式，因此不同稀疏模式会产生不同消去树。

spy(A(r,r))
title("Reverse Cuthill-McKee Sparsity Pattern")

Figure contains an axes object. The axes object with title Reverse Cuthill-McKee Sparsity Pattern, xlabel nz = 180 contains a line object which displays its values using only markers.

spy(A(m,m))
title("Minimum Degree Sparsity Pattern")

Figure contains an axes object. The axes object with title Minimum Degree Sparsity Pattern, xlabel nz = 180 contains a line object which displays its values using only markers.

输入参数

全部折叠

输入矩阵。A 可以是满矩阵，也可以是稀疏矩阵。如果消去树类型是 "sym" 或 "lo"，则 A 必须为方阵。etree 使用 A 的稀疏结构来计算消去树。

数据类型: double | logical
复数支持: 是

消去树的类型，指定为 "sym"、"lo"、"col" 或 "row"。使用此参量指定矩阵 etree 使用哪种方式计算消去树。

  • 如果 type 是 "sym"，则 etree 使用 A 的上三角构造对称方阵，并返回该矩阵的消去树。

  • 如果 type 是 "lo"，则 etree 使用 A 的下三角构造对称方阵，并返回该矩阵的消去树。

  • 如果 type 是 "col"，则 etree 构造矩阵 A'*A 并返回该矩阵的消去树，也就是 A 的列消去树。

  • 如果 type 是 "row"，则 etree 构造矩阵 A*A' 并返回该矩阵的消去树，也就是 A 的行消去树。

输出参量

全部折叠

消去树，以数值向量形式返回。p(i) 表示树中节点 i 的父级，如果 i 是根节点，则为 0。

消去树 p 的后序排列，以数值向量形式返回。

手动计算乔列斯基分解的列时，可以使用消去树的后序排列。对于消去树 p 中的节点 i 及其父节点 j，在乔列斯基分解中，必须先完全计算出列 i，然后才能计算列 j。p 的后序排列指定了一个计算这些列的顺序，该顺序与此要求一致。使用 chol 直接计算分解。

详细信息

全部折叠

消去树

消去树是一种数据结构体，它捕获乔列斯基分解的行和列依存关系，并描述可以同时执行的运算。消去树的不相交分支可以并行计算，因此具有分支的消去树的矩阵分解可以更快地计算。您可以对稀疏矩阵重新排序，以更改填充量并计算一个不同的消去树。

参考

[1] Chen, Yanqing, Timothy A. Davis, William W. Hager, and Sivasankaran Rajamanickam. “Algorithm 887: CHOLMOD, Supernodal Sparse Cholesky Factorization and Update/Downdate.” ACM Transactions on Mathematical Software 35, no. 3 (October 2008): 1–14. https://doi.org/10.1145/1391989.1391995.

[2] Pothen, Alex, and Sivan Toledo. "Elimination Structures in Scientific Computing." In Handbook of Data Structures and Applications, edited by Dinesh P. Mehta and Sartaj Sahni, 945–965. New York: Chapman and Hall/CRC, 2017. https://doi.org/10.1201/9781315119335

扩展功能

版本历史记录

在 R2006a 之前推出

另请参阅

| | |