Main Content

chol

Cholesky 分解

全页折叠

语法

R = chol(A)
R = chol(A,triangle)
[R,flag] = chol(___)
[R,flag,P] = chol(S)
[R,flag,P] = chol(___,outputForm)

说明

示例

R = chol(A) 将对称正定矩阵 A 分解成满足 A = R'*R 的上三角 R。如果 A 是非对称矩阵，则 chol 将矩阵视为对称矩阵，并且只使用 A 的对角线和上三角。

示例

R = chol(A,triangle) 指定在计算分解时使用 A 的哪个三角因子。例如，如果 triangle 是 'lower'，则 chol 仅使用 A 的对角线和下三角部分来生成满足 A = R*R' 的下三角矩阵 R。triangle 的默认值是 'upper'。

示例

[R,flag] = chol(___) 还返回输出 flag，指示 A 是否为对称正定矩阵。您可以使用上述语法中的任何输入参数组合。当您指定 flag 输出时，如果输入矩阵不是对称正定矩阵，chol 不会生成错误。

  • 如果 flag = 0，则输入矩阵是对称正定矩阵，分解成功。

  • 如果 flag 不为零，则输入矩阵不是对称正定矩阵，flag 为整数，表示分解失败的主元位置的索引。

示例

[R,flag,P] = chol(S) 另外返回一个置换矩阵 P，这是 amd 获得的稀疏矩阵 S 的预先排序。如果 flag = 0，则 S 是对称正定矩阵，R 是满足 R'*R = P'*S*P 的上三角矩阵。

示例

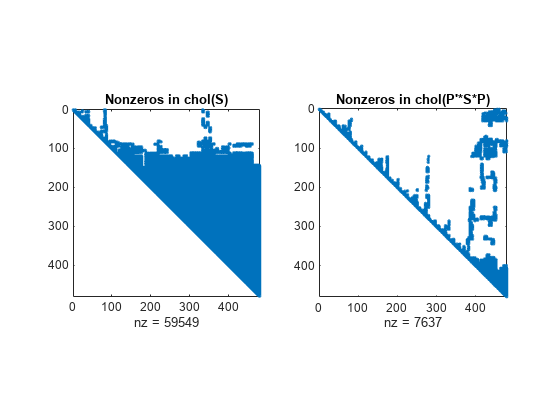
[R,flag,P] = chol(___,outputForm) 使用上述语法中的任何输入参数组合，指定是以矩阵还是向量形式返回置换信息 P。此选项仅可用于稀疏矩阵输入。例如，如果 outputForm 是 'vector' 且 flag = 0，则 S(p,p) = R'*R。outputForm 的默认值是 'matrix'，满足 R'*R = P'*S*P。

示例

全部折叠

打开实时脚本

使用 chol 分解对称系数矩阵，然后使用 Cholesky 因子求解线性系统。

创建在对角线上为正值的对称矩阵。

A = [1 0 1; 0 2 0; 1 0 3]
A = 3×3

     1     0     1
     0     2     0
     1     0     3

计算矩阵的 Cholesky 因子。

R = chol(A)
R = 3×3

    1.0000         0    1.0000
         0    1.4142         0
         0         0    1.4142

为方程 Ax=b 的右侧创建一个向量。

b = sum(A,2);

由于 A=RTR 具有 Cholesky 分解，该线性方程变为 RTR x=b。使用反斜杠运算符求解 x。

x = R\(R'\b)
x = 3×1

    1.0000
    1.0000
    1.0000
打开实时脚本

计算矩阵的上下 Cholesky 分解，并验证结果。

使用 gallery 函数创建一个 6×6 对称正定测试矩阵。

A = gallery('lehmer',6);

使用 A 的上三角计算 Cholesky 因子。

R = chol(A)
R = 6×6

    1.0000    0.5000    0.3333    0.2500    0.2000    0.1667
         0    0.8660    0.5774    0.4330    0.3464    0.2887
         0         0    0.7454    0.5590    0.4472    0.3727
         0         0         0    0.6614    0.5292    0.4410
         0         0         0         0    0.6000    0.5000
         0         0         0         0         0    0.5528

验证上三角因子满足 R'*R - A = 0（在舍入误差内）。

norm(R'*R - A)
ans = 2.5801e-16

现在，指定 'lower' 选项以使用 A 的下三角形计算 Cholesky 因子。

L = chol(A,'lower')
L = 6×6

    1.0000         0         0         0         0         0
    0.5000    0.8660         0         0         0         0
    0.3333    0.5774    0.7454         0         0         0
    0.2500    0.4330    0.5590    0.6614         0         0
    0.2000    0.3464    0.4472    0.5292    0.6000         0
    0.1667    0.2887    0.3727    0.4410    0.5000    0.5528

验证下三角因子满足 L*L' - A = 0（在舍入误差内）。

norm(L*L' - A)
ans = 2.5801e-16
打开实时脚本

当输入矩阵不是对称正定矩阵时，使用带两个输出的 chol 来隐藏错误。

创建一个 5×5 二项式系数矩阵。此矩阵是对称正定矩阵，因此我们从最后一个元素中减去 1 以使它不再是正定矩阵。

A = pascal(5);
A(end) = A(end) - 1
A = 5×5

     1     1     1     1     1
     1     2     3     4     5
     1     3     6    10    15
     1     4    10    20    35
     1     5    15    35    69

计算 A 的 Cholesky 因子。如果 A 不是对称正定矩阵，请指定两个输出以避免生成错误。

[R,flag] = chol(A)
R = 4×4

     1     1     1     1
     0     1     2     3
     0     0     1     3
     0     0     0     1


flag = 5

由于 flag 为非零，因此它给出了分解失败所在位置的主元索引。chol 能够正确计算 q = flag-1 = 4 个行和列，然后在遇到矩阵中发生了变化的部分时失败。

验证 R'*R 返回的四行四列与 A(1:q,1:q) 一致。

q = flag-1;
R'*R
ans = 4×4

     1     1     1     1
     1     2     3     4
     1     3     6    10
     1     4    10    20


A(1:q,1:q)
ans = 4×4

     1     1     1     1
     1     2     3     4
     1     3     6    10
     1     4    10    20
打开实时脚本

计算稀疏矩阵的 Cholesky 因子，并使用置换输出创建具有较少非零元素的 Cholesky 因子。

基于 west0479 矩阵创建一个稀疏正定矩阵。

load west0479
A = west0479;
S = A'*A;

用两种不同方法计算矩阵的 Cholesky 因子。首先指定两个输出，然后指定三个输出以支持行和列重新排序。 

[R,flag] = chol(S);
[RP,flagP,P] = chol(S);

对于每次计算，都检查 flag = 0 以确认计算成功。

if ~flag && ~flagP
    disp('Factorizations successful.')
else
    disp('Factorizations failed.')
end
Factorizations successful.

比较 chol(S) 和经过重新排序的矩阵 chol(P'*S*P) 中非零元素的个数。最佳做法是对稀疏矩阵使用 chol 的带三个输出的语法，因为对行和列重新排序会大大减少 Cholesky 因子中的非零元素个数。

subplot(1,2,1)
spy(R)
title('Nonzeros in chol(S)')
subplot(1,2,2)
spy(RP)
title('Nonzeros in chol(P''*S*P)')

Figure contains 2 axes objects. axes object 1 with title Nonzeros in chol(S), xlabel nz = 59550 contains a line object which displays its values using only markers. axes object 2 with title Nonzeros in chol(P'*S*P), xlabel nz = 7637 contains a line object which displays its values using only markers.

打开实时脚本

使用 chol 的 'vector' 选项以向量而不是矩阵形式返回置换信息。

创建一个稀疏有限元矩阵。

S = gallery('wathen',10,10);
spy(S)

Figure contains an axes object. The axes object with xlabel nz = 4861 contains a line object which displays its values using only markers.

计算矩阵的 Cholesky 因子，并指定 'vector' 选项以返回置换向量 p。

[R,flag,p] = chol(S,'vector');

验证 flag = 0，表明计算成功。 

if ~flag
    disp('Factorization successful.')
else
    disp('Factorization failed.')
end
Factorization successful.

验证 S(p,p) = R'*R（在舍入误差内）。

norm(S(p,p) - R'*R,'fro')
ans = 2.1039e-13

输入参数

全部折叠

输入矩阵。参数 A 可以使用满存储或稀疏存储，但必须为方阵和对称正定矩阵。

chol 假设 A 是对称实矩阵，或者是 Hermitian 对称复矩阵。chol 仅使用 A 的上三角或下三角执行计算，具体取决于 triangle 的值。

数据类型： single | double
复数支持： 是

稀疏输入矩阵。S 必须为方阵和对称正定矩阵。

chol 假设 S 是对称实矩阵，或者是 Hermitian 对称复矩阵。chol 仅使用 S 的上三角或下三角执行计算，具体取决于 triangle 的值。

数据类型： double
复数支持： 是

输入矩阵的三角因子，指定为 'upper' 或 'lower'。使用此选项指定 chol 应使用输入矩阵的上三角或下三角来计算分解。chol 假设输入矩阵是对称实矩阵或 Hermitian 复矩阵。chol 仅使用上三角或下三角执行计算。

使用 'lower' 选项相当于使用 'upper' 选项和输入矩阵转置调用 chol，然后转置输出 R。

示例： R = chol(A,'lower')

置换输出的形状，指定为 'matrix' 或 'vector'。此标志控制置换输出 P 是以置换矩阵还是置换向量形式返回。

  • 如果 flag = 0，则 S 是对称正定矩阵且 P'*S*P = R'*R（如果 P 是矩阵）或 S(p,p) = R'*R（如果 p 是向量）。

  • 如果 flag 不为零，则 S 不是对称正定矩阵。R 是上三角矩阵，大小为 q×n，其中 q = flag-1。R'*R 的前 q 行和前 q 列的 L 形区域与 P'*S*P（如果 P 是矩阵）或 S(p,p)（如果 p 是向量）的大小一致。

  • 如果指定 'lower' 选项，则 R 是下三角矩阵，您可以用之前的恒等式中的 R*R' 替换 R'*R。

P'*S*P（如果 P 是矩阵）或 S(p,p)（如果 p 是向量）的 Cholesky 因子可能比 S 的 Cholesky 因子稀疏。

示例： [R,flag,p] = chol(S,'vector')

输出参数

全部折叠

Cholesky 因子，以矩阵形式返回。

  • 如果 R 是上三角矩阵，则 A = R'*R。如果您为稀疏矩阵指定 P 输出，则 P'*S*P = R'*R 或 S(p,p) = R'*R，具体取决于 outputForm 的值。

  • 如果 R 是下三角矩阵，则 A = R*R'。如果您为稀疏矩阵指定 P 输出，则 P'*S*P = R*R' 或 S(p,p) = R*R'，具体取决于 outputForm 的值。

  • 如果 flag 不为零，R 将仅包含部分结果。flag 指示分解失败的主元位置，R 包含部分完成的分解。

对称正定标志，以标量形式返回。

  • 如果 flag = 0，则输入矩阵是对称正定矩阵。R 是上三角矩阵，满足 R'*R = A。

  • 如果 A 不是对称正定矩阵，则 flag 为一个正整数，指示分解失败的主元位置，并且 MATLAB® 不会生成错误。R 是大小为 q = flag-1 的上三角矩阵，满足 R'*R = A(1:q,1:q)。

  • 如果 A 为稀疏矩阵，则 R 是大小为 q×n 的上三角矩阵，这样 R'*R 的前 q 行和前 q 列的 L 形区域与 A 或 S 的大小一致。

  • 如果指定 'lower' 选项，则 R 是下三角矩阵，您可以用之前的恒等式中的 R*R' 替换 R'*R。

稀疏矩阵的置换，以矩阵或向量形式返回，具体取决于 outputForm 的值。有关此输出满足的恒等式的说明，请参阅 outputForm。

该置换矩阵基于 amd 计算的近似最小度排序。但是，这种预先排序可能不同于直接通过 amd 获得的排序，因为 chol 会略微更改排序以提高性能。

详细信息

全部折叠

对称正定矩阵

对称正定矩阵是所有特征值均为正值的对称矩阵。

对于任何可逆实矩阵 A，您可以用乘积 B = A'*A 构造一个对称正定矩阵。由于任何对称正定矩阵 B 都可以分解为乘积 R'*R，Cholesky 分解可对此公式求反。

对称半正定矩阵的定义与此类似，只是其特征值必须均为正值或零。

在数值计算中，正定矩阵和半正定矩阵之间的界限比较模糊。特征值精确等于零的情况很少见，但它们可以在数值上为零（在计算机精度的数量级上）。因此，chol 可能能够分解一个半正定矩阵，但对于特征值非常相似的另一个矩阵，分解可能会失败。

提示

参考

[1] Anderson, E., ed. LAPACK Users’ Guide. 3rd ed. Software, Environments, Tools. Philadelphia: Society for Industrial and Applied Mathematics, 1999. https://doi.org/10.1137/1.9780898719604.

[2] Chen, Yanqing, Timothy A. Davis, William W. Hager, and Sivasankaran Rajamanickam. “Algorithm 887: CHOLMOD, Supernodal Sparse Cholesky Factorization and Update/Downdate.” ACM Transactions on Mathematical Software 35, no. 3 (October 2008): 1–14. https://doi.org/10.1145/1391989.1391995.

扩展功能

版本历史记录

在 R2006a 之前推出

另请参阅

| | |

主题