ichol

不完全乔列斯基分解

全页折叠

语法

L = ichol(A)

L = ichol(A,options)

说明

L = ichol(A) 通过零填充执行 A 的不完全乔列斯基分解。A 必须为稀疏方阵。

示例

L = ichol(A,options) 使用结构图 options 指定的选项对 A 执行不完全乔列斯基分解。

默认情况下，ichol 引用 A 的下三角并生成下三角因子。

示例

全部折叠

不完全乔列斯基分解

打开实时脚本

此示例生成不完全乔列斯基分解。

从一个对称正定矩阵 A 开始：

N = 100;
A = delsq(numgrid('S',N));

A 是带有狄利克雷边界条件的 100×100 方形网格上的二维、五点离散负拉普拉斯矩阵。A 的大小为 98*98 = 9604（并非 10000，因为网格边框用于施加狄利克雷条件）。

无填充的不完全乔列斯基分解是指在 A 包含非零值的相同位置仅包含非零值的分解。此分解的计算非常容易。尽管 L*L' 乘积通常与 A 完全不同，但 L*L' 乘积将与 A 在其向上舍入模式上匹配。

L = ichol(A);
norm(A-L*L','fro')./norm(A,'fro')

ans = 
0.0916

norm(A-(L*L').*spones(A),'fro')./norm(A,'fro')

ans = 
4.9606e-17

ichol 也可用于通过阈值调降生成不完全乔列斯基分解。当调降容差减小时，因子往往会变得更密集，而 L*L' 乘积往往更好地接近 A。以下绘图显示了不完全分解的相对误差对调降容差的图，以及不完全因子密度与完全乔列斯基因子密度之比。

n = size(A,1);
ntols = 20;
droptol = logspace(-8,0,ntols);
nrm = zeros(1,ntols);
nz = zeros(1,ntols);
nzComplete = nnz(chol(A,'lower'));
for k = 1:ntols
    L = ichol(A,struct('type','ict','droptol',droptol(k)));
    nz(k) = nnz(L);
    nrm(k) = norm(A-L*L','fro')./norm(A,'fro');
end
figure
loglog(droptol,nrm,'LineWidth',2)
title('Drop tolerance vs norm(A-L*L'',''fro'')./norm(A,''fro'')')

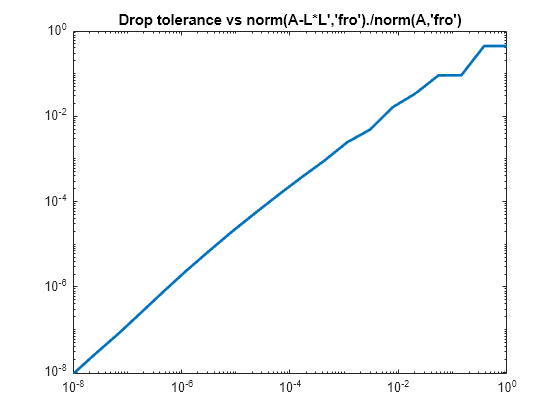
Figure contains an axes object. The axes object with title Drop tolerance vs norm(A-L*L','fro')./norm(A,'fro') contains an object of type line.

figure
semilogx(droptol,nz./nzComplete,'LineWidth',2)
title('Drop tolerance vs fill ratio ichol/chol')

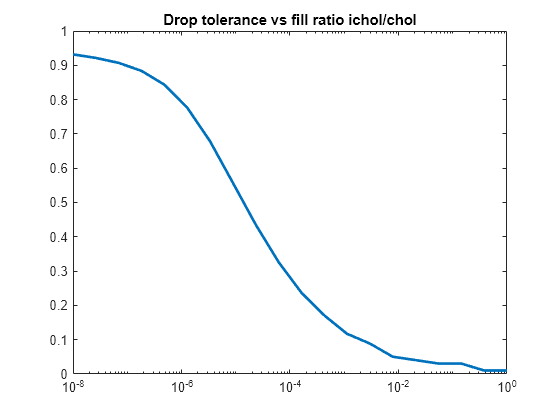
Figure contains an axes object. The axes object with title Drop tolerance vs fill ratio ichol/chol contains an object of type line.

该相对误差通常与调降容差的量级相当，但不能保证一定如此。

使用 `ichol` 作为预条件子

打开实时脚本

此示例说明如何使用不完全乔列斯基分解作为预条件子来提高收敛。

创建一个对称正定矩阵 A。

N = 100;
A = delsq(numgrid('S',N));

创建一个不完全乔列斯基分解，作为 pcg 的预条件子。在右侧使用一个常向量。先在没有预条件子的情况下执行 pcg，以作为基准。

b = ones(size(A,1),1);
tol = 1e-6;
maxit = 100;
[x0,fl0,rr0,it0,rv0] = pcg(A,b,tol,maxit);

请注意，fl0 = 1 指示 pcg 未在允许的最大迭代次数中使相对残差趋向于请求的容差。请尝试使用无填充的不完全乔列斯基分解作为预条件子。

L1 = ichol(A);
[x1,fl1,rr1,it1,rv1] = pcg(A,b,tol,maxit,L1,L1');

fl1 = 0，指示 pcg 收敛至请求的容差，经过 59 次迭代（it1 值）后实现收敛。但是，由于此矩阵是一个离散的拉普拉斯矩阵，因此使用修正不完全乔列斯基分解可创建一个更好的预条件子。修正不完全乔列斯基分解会构造一个近似的分解，该分解会保留算子对常向量的作用。也就是说，对于 e = ones(size(A,2),1)，norm(A*e-L*(L'*e)) 将约为零，即使 norm(A-L*L','fro')/norm(A,'fro') 不接近零。不必为此语法指定类型，因为 nofill 是默认值，但这是一种好的做法。

options.type = 'nofill';
options.michol = 'on';
L2 = ichol(A,options);
e = ones(size(A,2),1);
norm(A*e-L2*(L2'*e))

ans = 
3.7983e-14

[x2,fl2,rr2,it2,rv2] = pcg(A,b,tol,maxit,L2,L2');

pcg 收敛 (fl2 = 0)，但仅用了 38 次迭代。绘制所有三种收敛历史记录将显示以下收敛情况。

semilogy(0:maxit,rv0./norm(b),'b.');
hold on
semilogy(0:it1,rv1./norm(b),'r.');
semilogy(0:it2,rv2./norm(b),'k.');
legend('No Preconditioner','IC(0)','MIC(0)');

Figure contains an axes object. The axes object contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent No Preconditioner, IC(0), MIC(0).

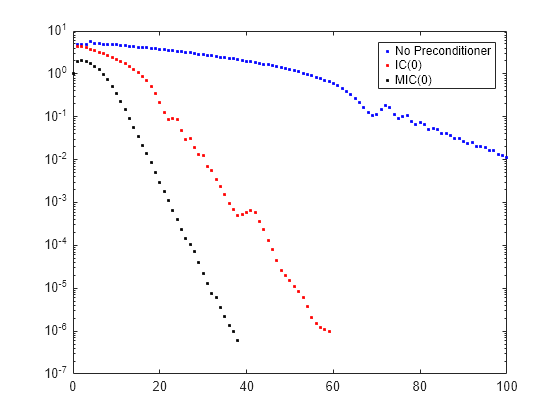
以上绘图显示，修正不完全乔列斯基预条件子创建的收敛更快。

您也可以尝试通过阈值调降使用不完全乔列斯基分解。以下绘图显示了通过各种调降容差构造预条件子时 pcg 的收敛。

L3 = ichol(A, struct('type','ict','droptol',1e-1));
[x3,fl3,rr3,it3,rv3] = pcg(A,b,tol,maxit,L3,L3');
L4 = ichol(A, struct('type','ict','droptol',1e-2));
[x4,fl4,rr4,it4,rv4] = pcg(A,b,tol,maxit,L4,L4');
L5 = ichol(A, struct('type','ict','droptol',1e-3));
[x5,fl5,rr5,it5,rv5] = pcg(A,b,tol,maxit,L5,L5'); 

figure
semilogy(0:maxit,rv0./norm(b),'b-','linewidth',2);
hold on
semilogy(0:it3,rv3./norm(b),'b-.','linewidth',2);
semilogy(0:it4,rv4./norm(b),'b--','linewidth',2);
semilogy(0:it5,rv5./norm(b),'b:','linewidth',2);
legend('No Preconditioner','ICT(1e-1)','ICT(1e-2)', ...
   'ICT(1e-3)','Location','SouthEast');

Figure contains an axes object. The axes object contains 4 objects of type line. These objects represent No Preconditioner, ICT(1e-1), ICT(1e-2), ICT(1e-3).

请注意，通过调降容差 1e-2 构造的不完全乔列斯基预条件子表示为 ICT(1e-2)。

与零填充的不完全乔列斯基分解一样，阈值调降分解也会受益于修正（即 options.michol = 'on'），因为矩阵由一个椭圆偏微分方程生成。与 MIC(0) 一样，修正后的阈值调降不完全乔列斯基分解也将保留预条件子对常向量的作用，也即 norm(A*e-L*(L'*e)) 将约为零。

使用 `diagcomp` 选项

打开实时脚本

此示例介绍了 ichol 的 diagcomp 选项的用法。

正定矩阵的不完全乔列斯基分解并不总是存在。以下代码构造一个随机的对称正定矩阵，并尝试使用 pcg 对线性系统求解。

S = rng('default');
A = sprandsym(1000,1e-2,1e-4,1);
rng(S);
b = full(sum(A,2));
[x0,fl0,rr0,it0,rv0] = pcg(A,b,1e-6,100);

由于未实现收敛，因此请尝试构造一个不完全乔列斯基预条件子。

L = ichol(A,struct('type','ict','droptol',1e-3));

Error using ichol
Encountered nonpositive pivot.

如果 ichol 按以上所示进行分解，您可以使用 diagcomp 选项构造一个偏移的不完全乔列斯基分解。也就是说，带有对角线补偿的 ichol 会构造 L 以使 L*L' 在未显式构造 M 的情况下约为 M = A + alpha*diag(diag(A))，而不是构造 L 以使 L*L' 约为 A。由于对于对角线占优的矩阵始终可以进行不完全分解，因此可以求得使 M 在对角线上占优的 alpha。

alpha = max(sum(abs(A),2)./diag(A))-2

alpha = 
62.9341

L1 = ichol(A, struct('type','ict','droptol',1e-3,'diagcomp',alpha));
[x1,fl1,rr1,it1,rv1] = pcg(A,b,1e-6,100,L1,L1');

此处的 pcg 仍然无法在所需的迭代次数内收敛至所需容差，但正如以下绘图所示，与没有预条件子相比，收敛更适用于带有此预条件子的 pcg。选择更小的 alpha 可能会有帮助。通过试验，我们可以为 alpha 设置合适的值。

alpha = .1;
L2 = ichol(A, struct('type','ict','droptol',1e-3,'diagcomp',alpha));
[x2,fl2,rr2,it2,rv2] = pcg(A,b,1e-6,100,L2,L2');

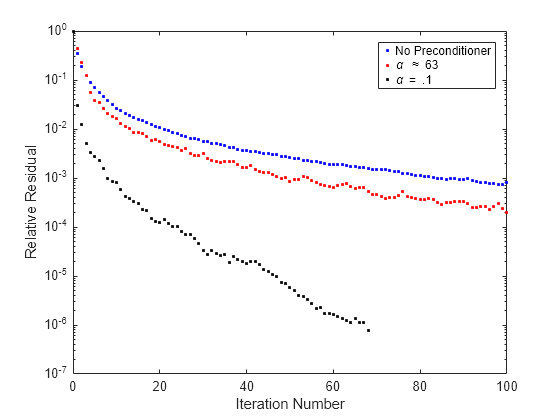
现在，pcg 将会收敛，并且绘图可以显示每个预条件子的收敛历史记录。

semilogy(0:100,rv0./norm(b),'b.');
hold on;
semilogy(0:100,rv1./norm(b),'r.');
semilogy(0:it2,rv2./norm(b),'k.');
legend('No Preconditioner','\alpha \approx 63','\alpha = .1');
xlabel('Iteration Number');
ylabel('Relative Residual');

$Figure contains an axes object. The axes object with xlabel Iteration Number, ylabel Relative Residual contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent No Preconditioner, \alpha \approx 63, \alpha = .1.$

输入参数

全部折叠

`A` — 输入矩阵
稀疏方阵

输入矩阵，指定为稀疏方阵。

数据类型: single | double
复数支持: 是

`options` — 乔列斯基分解选项
结构体

乔列斯基分解选项，指定为包含最多五个字段的结构体：

字段名称	摘要	描述
`type`	分解的类型	指示要执行的不完全乔列斯基分解类型。此字段的有效值为 `'nofill'` 和 `'ict'`。`'nofill'` 变体执行零填充的不完全乔列斯基分解 (`IC(0)`)。`'ict'` 变体执行使用阈值调降的不完全乔列斯基分解 (ICT)。默认值为 `'nofill'`。
`droptol`	类型为 `'ict'` 时的调降容差	执行 ICT 时用作调降容差的非负标量。如果元素的模小于局部调降容差，它将从生成的因子中删除，但对角线元素除外，该元素永不会被删除。分解的第 `j` 步的局部调降容差为 `norm(A(j:end,j),1)*droptol`。如果 `'type'` 为 `'nofill'`，则会忽略 `'droptol'`。默认值为 `0`。
`michol`	指示是否执行修正的不完全乔列斯基分解	指示是否执行修正的不完全乔列斯基分解 (MIC)。该字段可能为 `'on'` 或 `'off'`。执行 MIC 时，将为对角线补偿所删除的元素，以实施关系 `Ae = LL'*e`，其中 `e = ones(size(A,2),1)`。默认值为 `'off'`。
`diagcomp`	使用指定的系数执行补偿的不完全乔列斯基分解	构造不完全乔列斯基因子时用作全局对角线偏移量 `alpha` 的非负实数标量。也就是说，不必对 `A` 执行不完全乔列斯基分解，即可构造 `A + alpha*diag(diag(A))` 分解。默认值为 `0`。
`shape`	确定引用并返回的三角矩阵	有效值为 `'upper'` 和 `'lower'`。如果指定 `'upper'`，则仅引用 `A` 的上三角矩阵并且会构造 `R`，以使 `A` 接近 `R'R`。如果指定 `'lower'`，则仅引用 `A` 的下三角矩阵并且会构造 `L`，以使 `A` 接近 `LL'`。默认值为 `'lower'`。

示例: options.type = 'nofill'; options.michol = 'on'; L = ichol(A,options);

提示

此例程提供的因子可能很有用，可用作通过 pcg 或 minres 等迭代方法求解的线性系统的预条件子。
ichol 仅适用于稀疏方阵。

参考

[1] Saad, Yousef. “Preconditioning Techniques.” Iterative Methods for Sparse Linear Systems. PWS Publishing Company, 1996.

[2] Manteuffel, T.A. “An incomplete factorization technique for positive definite linear systems.” Math. Comput. 34, 473–497, 1980.

扩展功能

全部展开

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

此函数完全支持基于线程的环境。有关详细信息，请参阅在基于线程的环境中运行 MATLAB 函数。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

用法说明和限制：

如果指定 options 的 type 字段，则它必须为 'nofill'。
A 必须为实对称矩阵或埃尔米特复矩阵。

有关详细信息，请参阅使用分布式数组运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2011a 中推出

全部展开

R2025a: 指定单精度稀疏输入参量

您可以将输入矩阵 A 指定为单精度。如果 A 为 single，则输出参量也为 single。

另请参阅

ilu | chol | pcg | minres

ichol

语法

说明

示例

不完全乔列斯基分解

使用 ichol 作为预条件子

使用 diagcomp 选项

输入参数

A — 输入矩阵 稀疏方阵

options — 乔列斯基分解选项 结构体

提示

参考

扩展功能

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

分布式数组 使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

版本历史记录

R2025a: 指定单精度稀疏输入参量

另请参阅

主题

使用 `ichol` 作为预条件子

使用 `diagcomp` 选项

`A` — 输入矩阵
稀疏方阵

`options` — 乔列斯基分解选项
结构体

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。