Main Content

matchpairs

求解线性分配问题

全页折叠

语法

M = matchpairs(Cost,costUnmatched)
[M,uR,uC] = matchpairs(Cost,costUnmatched)
[___] = matchpairs(Cost,costUnmatched,goal)

说明

示例

M = matchpairs(Cost,costUnmatched) 求解矩阵 Cost 的行和列的线性分配问题。该函数按总成本最小的方法将每行分配给一列。costUnmatched 指定存在未分配行时的每行成本，以及存在未分配行的列时的每列成本。

[M,uR,uC] = matchpairs(Cost,costUnmatched) 还返回 uR 中未匹配行的索引和 uC 中未匹配列的索引。

示例

[___] = matchpairs(Cost,costUnmatched,goal) 指定优化目标，并可使用上述语法中的任何输出参量组合。goal 可以是 'min' 或 'max' 以生成总成本最小化或最大化的匹配。

示例

全部折叠

打开实时脚本

将销售人员分配到各个航班，使总交通成本最小化。

一家公司有四名销售人员，他们需要去全国主要城市出差。该公司必须为他们预订航班，并希望费用支出尽可能少。这些销售人员分布在全国不同地方，因此他们飞往每个城市的费用各不相同。

下表显示了每位销售人员飞往每个主要城市的成本。

DallasChicagoNew York CitySt. LouisFred$600$670$960$560Beth$900$280$970$540Sue$310$350$950$820Greg$325$290$600$540

每个城市都代表一个销售机会。如果错过一个城市，则该公司将损失平均 2,000 美元的收益。

创建一个成本矩阵来表示每位销售人员飞往每个城市的成本。

C = [600 670 960 560
     900 280 970 540
     310 350 950 820
     325 290 600 540];

使用 matchpairs 将销售人员分配到各个城市并使成本最小。将未分配成本指定为 1,000，因为如果有一行和一列未匹配，则计两次未分配成本。

M = matchpairs(C,1000)
M = 4×2

     3     1
     2     2
     4     3
     1     4

matchpairs 计算为每个城市分配一位销售人员的最经济的方式。

DallasChicagoNew York CitySt. LouisFred$600$670$960$560Beth$900$280$970$540Sue$310$350$950$820Greg$325$290$600$540

打开实时脚本

当成本矩阵中的列数远多于行数时，请将行匹配到列。

创建一个 3×8 成本矩阵。由于只有三行，对于八列，matchpairs 最多只能产生三个匹配。

rng default % for reproducibility
C = randi([10 100], 3, 8)
C = 3×8

    84    93    35    97    97    22    82    13
    92    67    59    24    54    48    97    87
    21    18    97    98    82    93    69    94

使用 matchpairs 匹配成本矩阵的行和列。要获得最大匹配数，请使用较大的未分配成本（相对于成本矩阵中各项的模）。指定三个输出以返回未匹配的行和列的索引。

[M,uR,uC] = matchpairs(C,1e4)
M = 3×2

     3     2
     2     4
     1     8


uR =

  0x1 empty double column vector

uC = 5×1

     1
     3
     5
     6
     7

C 中有五列不匹配任何行。

打开实时脚本

为路线分配出租车，使利润最大化。

一家出租车公司有几个来自市内各地的乘车请求。该公司希望以最赚钱的方式派遣数量有限的出租车。

下表显示了五个乘车请求中每个请求的出租车费估计值。五个乘车请求中只有三个可以得到满足。

Ride 1Ride 2Ride 3Ride 4Ride 5Cab A$5.70$6.30$3.10$4.80$3.50Cab B$5.80$6.40$3.30$4.70$3.20Cab C$5.70$6.30$3.20$4.90$3.40

创建一个利润矩阵来表示每个行程的利润。

P = [5.7 6.3 3.1 4.8 3.5
     5.8 6.4 3.3 4.7 3.2
     5.7 6.3 3.2 4.9 3.4];

使用 matchpairs 将出租车匹配到最赚钱的行程。指定三个输出以返回未匹配的行和列，并使用 'max' 选项以最大化利润。将未分配成本指定为零，因为公司不会从未载客的出租车或未满足的乘车请求中赚钱。

costUnmatched = 0;
[M,uR,uC] = matchpairs(P,costUnmatched,'max')
M = 3×2

     1     1
     2     2
     3     4


uR =

  0x1 empty double column vector

uC = 2×1

     3
     5

matchpairs 计算最赚钱的乘车分配方式。在该解中，第 3 和第 5 个乘车请求未得到满足。

Ride 1Ride 2Ride 3Ride 4Ride 5Cab A$5.70$6.30$3.10$4.80$3.50Cab B$5.80$6.40$3.30$4.70$3.20Cab C$5.70$6.30$3.20$4.90$3.40

根据求出的解计算总利润。由于 costUnmatched 为零，您只需将每个匹配的利润相加即可。

TotalProfits = sum(P(sub2ind(size(P), M(:,1), M(:,2))))
TotalProfits = 17
打开实时脚本

使用 matchpairs 跟踪几个点的移动，使距离的总变化最小。

用绿色绘制时间 t=0 时的网格点。时间 t=1 时，一些点在随机方向上移动一小段距离。

[x,y] = meshgrid(4:6:16);
x0 = x(:)';
y0 = y(:)';
plot(x0,y0,'g*')
hold on
rng default % for reproducibility
x1 = x0 + randn(size(x0));
y1 = y0 + randn(size(y0));
plot(x1,y1,'r*')

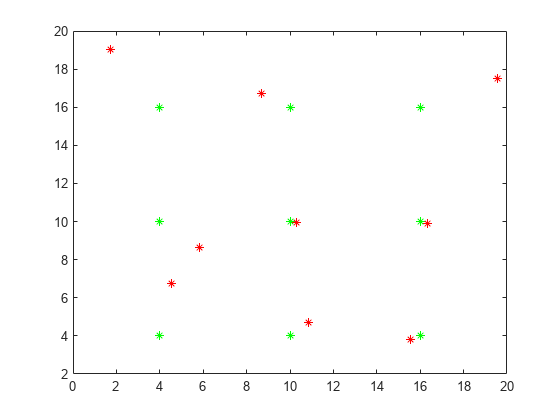
使用 matchpairs 将 t=0 时的点与 t=1 时的点进行匹配。为此，首先计算一个成本矩阵，其中 C(i,j) 是从 i 点到 j 点的欧几里德距离。

C = zeros(size(x).^2);
for k = 1:length(y1)
  C(k,:) = vecnorm([x1(k)-x0; y1(k)-y0],2,1)';
end
C
C = 9×9

    2.8211    3.2750    9.2462    6.1243    6.3461   10.7257   11.7922   11.9089   14.7169
    4.9987    2.2771    7.5752    6.2434    4.3794    8.4485   11.1792   10.2553   12.5447
   15.2037    9.3130    3.7833   17.1539   12.2408    8.7988   20.7211   16.8803   14.5783
    6.9004    8.6551   13.1987    1.1267    5.3446   11.3075    5.1888    7.3633   12.3901
    8.6703    6.3191    8.7571    5.9455    0.3249    6.0714    8.2173    5.6816    8.3089
   13.5530    8.1918    4.7464   12.7818    6.8409    1.4903   14.6652    9.9242    7.3426
   11.5682   13.1257   16.8150    5.5702    8.3359   13.4144    0.4796    6.2201   12.2127
   13.6699   12.3432   13.7784    8.6461    6.3438    8.8167    5.8858    0.3644    6.1337
   20.6072   17.2853   15.6495   16.5444   12.1590    9.6935   13.9562    8.3006    3.8761

接下来，使用 matchpairs 匹配成本矩阵中的行和列。将未分配成本指定为 1。相对于成本矩阵中的项，未分配成本非常低，matchpairs 很可能会留下一些不匹配的点。

M = matchpairs(C,1)
M = 5×2

     4     4
     5     5
     6     6
     7     7
     8     8

值 M(:,2) 对应于原始点 (x0,y0)，而值 M(:,1) 对应于移动后的点 (x1,y1)。

绘制匹配的点对组。相对原始点移动的距离超过 2*costUnmatched 的点保持未匹配。

xc = [x0(M(:,2)); x1(M(:,1))];
yc = [y0(M(:,2)); y1(M(:,1))];
plot(xc,yc,'-o')

输入参数

全部折叠

成本矩阵。每个项 Cost(i,j) 指定将 i 行分配给 j 列的成本。

数据类型: single | double

未匹配成本，指定为标量。matchpairs 将 2*costUnmatched 的值与 Cost 中的项进行比较，以确定某行或列保持未匹配是否更有利。使用此参数调整算法中匹配发生的可能性。有关详细信息，请参阅线性分配问题。

示例: M = matchpairs(C,10) 将 C 的行或列的未匹配成本指定为 10。

数据类型: single | double

优化目标，指定为 'min' 或 'max'。优化目标指定总成本应该最小化还是最大化。

示例: M = matchpairs(Cost,costUnmatched,'max') 指定 Cost 的行和列应以最大化总成本的方式进行匹配。

输出参量

全部折叠

匹配，以矩阵形式返回。M 是 p×2 矩阵，其中 M(i,1) 和 M(i,2) 是成本矩阵中匹配对组的行和列索引。M 的行按第二列升序排序。

  • 每行和每列只能匹配一次，因此每个 M(i,1) 值和每个 M(i,2) 值均唯一。

  • M 包含 p 个匹配，p 小于或等于最大匹配数 min(size(Cost))。

  • M 中的匹配成本是 sum([Cost(M(1,1),M(1,2)), Cost(M(2,1),M(2,2)), ..., Cost(M(p,1),M(p,2))])。

未分配的行，以索引的列向量形式返回。uR 中的项指示 Cost 中哪些行未分配。uR 和 uC 中的每项通过 costUnassigned 计入解的总成本。

未分配的列，以索引的列向量形式返回。uC 中的项指示 Cost 中哪些列未分配。uR 和 uC 中的每项通过 costUnassigned 计入解的总成本。

详细信息

全部折叠

线性分配问题

线性分配问题是一种将行分配给列的方法，要求每行都分配给一列，并且分配的总成本最小化（或最大化）。将每行分配给每列的成本记录在成本矩阵中。项 Cost(i,j) 是将 i 行分配给 j 列的成本。

未分配成本为每个未匹配的行或列分配一个成本。这种做法允许包含未分配行或列的最低成本解。如果某个行和列未匹配，这会使总成本增加 2*costUnmatched。

解 M 的总成本是所有已匹配对组的成本加上所有未匹配对组的成本之和：

TC=∑i=1pCost(M(i,1),M(i,2))+costUnmatched ⋅ (m+n−2p)

总成本用代码表示为

CostAssigned = sum(Cost(sub2ind(size(Cost), M(:,1), M(:,2))));
CostUnassigned = costUnmatched*(sum(size(Cost))-2*size(M,1));
TotalCost = CostAssigned + CostUnassigned;

  • Cost 是 m×n 矩阵。

  • M 是 p×2 矩阵，其中 M(i,1) 和 M(i,2) 是一个匹配对组的行和列。

  • (m+n-2*p) 是未匹配的行和列的总数。

参考

[1] Duff, I.S. and J. Koster. "On Algorithms For Permuting Large Entries to the Diagonal of a Sparse Matrix." SIAM J. Matrix Anal. & Appl. 22(4), 2001. pp 973–996.

扩展功能

版本历史记录

在 R2019a 中推出

另请参阅

| |