equilibrate
缩放矩阵以改善条件
说明
示例
平衡具有较大的条件数的矩阵,以提高用迭代求解器 gmres 求解线性系统的效率和稳定性。
加载 west0479 矩阵,这是一个实数值 479×479 稀疏矩阵。使用 condest 计算矩阵的估计条件数。
load west0479
A = west0479;
c1 = condest(A)c1 = 1.4244e+12
尝试使用 gmres 求解线性系统 ,迭代 450 次,容差为 1e-11。指定五个输出,以便 gmres 在每次迭代中返回解的残差范数(使用 ~ 隐藏不需要的输出)。在半对数图中绘制残差范数。该图显示,gmres 无法实现合理的残差范数,因此对 计算得出的解不可靠。
b = ones(size(A,1),1);
tol = 1e-11;
maxit = 450;
[x,flx,~,~,rvx] = gmres(A,b,[],tol,maxit);
semilogy(rvx)
title('Residual Norm at Each Iteration')
使用 equilibrate 置换和重新缩放 A。创建新矩阵 B = R*P*A*C,它具有更好的条件数且对角线上元素只有 1 和 -1。
[P,R,C] = equilibrate(A); B = R*P*A*C; c2 = condest(B)
c2 = 5.1036e+04
使用 equilibrate 返回的输出,您可以将问题 重新表示为 ,其中 且 。在此形式中,您可以使用 恢复原始方程组的解。然而,恢复的解可能不具有原始方程组所需的残差。有关详细信息,请参阅重新缩放以求解线性系统。
使用 gmres 求解 以得出 ,然后重新绘制每次迭代的残差范数。该图显示,对矩阵进行平衡处理提高了问题的稳定性,gmres 在不到 200 次迭代中收敛于期望容差 1e-11。
d = R*P*b; [y,fly,~,~,rvy] = gmres(B,d,[],tol,maxit); hold on semilogy(rvy) legend('Original', 'Equilibrated', 'Location', 'southeast') title('Relative Residual Norms (No Preconditioner)') hold off

使用预条件子改进解
获得矩阵 B 后,要进一步提高问题的稳定性,您可以计算预条件子并将其与 gmres 结合使用。B 的数值属性优于原始矩阵 A 的数值属性,因此您应该使用经平衡处理的矩阵来计算预条件子。
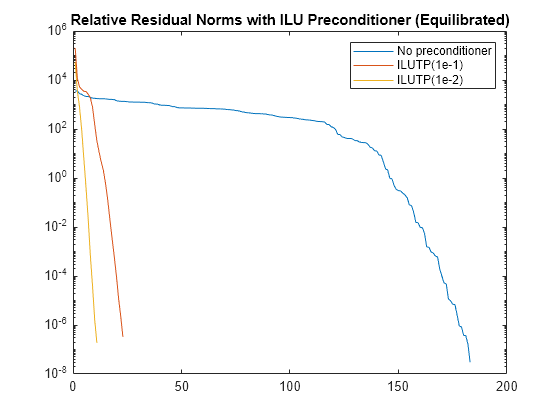
用 ilu 算出两个不同的预条件子,并将它们用作 gmres 的输入来再次求解问题。在绘制了平衡后范数的同一张图上,叠加绘制应用预条件子后每次迭代的残差范数,以进行比较。该图显示,基于经平衡处理的矩阵算出的预条件子极大地提高了问题的稳定性,gmres 在不到 30 次迭代中达到了所需的容差。
semilogy(rvy) hold on [L1,U1] = ilu(B,struct('type','ilutp','droptol',1e-1,'thresh',0)); [yp1,flyp1,~,~,rvyp1] = gmres(B,d,[],tol,maxit,L1,U1); semilogy(rvyp1) [L2,U2] = ilu(B,struct('type','ilutp','droptol',1e-2,'thresh',0)); [yp2,flyp2,~,~,rvyp2] = gmres(B,d,[],tol,maxit,L2,U2); semilogy(rvyp2) legend('No preconditioner', 'ILUTP(1e-1)', 'ILUTP(1e-2)') title('Relative Residual Norms with ILU Preconditioner (Equilibrated)') hold off
创建一个 6×6 幻方矩阵,然后使用 equilibrate 对该矩阵进行分解。默认情况下,equilibrate 以矩阵形式返回置换因子和缩放因子。
A = magic(6)
A = 6×6
35 1 6 26 19 24
3 32 7 21 23 25
31 9 2 22 27 20
8 28 33 17 10 15
30 5 34 12 14 16
4 36 29 13 18 11
[P,R,C] = equilibrate(A)
P = 6×6
0 0 0 0 1 0
0 0 0 0 0 1
0 0 0 1 0 0
1 0 0 0 0 0
0 0 1 0 0 0
0 1 0 0 0 0
R = 6×6
0.1852 0 0 0 0 0
0 0.1749 0 0 0 0
0 0 0.1909 0 0 0
0 0 0 0.1588 0 0
0 0 0 0 0.1793 0
0 0 0 0 0 0.1966
C = 6×6
0.1799 0 0 0 0 0
0 0.1588 0 0 0 0
0 0 0.1588 0 0 0
0 0 0 0.2422 0 0
0 0 0 0 0.2066 0
0 0 0 0 0 0.2035
使用矩阵因子 P、R 和 C 构造经平衡处理的矩阵 Bmatrix。
Bmatrix = R*P*A*C
Bmatrix = 6×6
1.0000 0.1471 1.0000 0.5385 0.5358 0.6031
0.1259 1.0000 0.8056 0.5509 0.6506 0.3916
0.2747 0.8485 1.0000 0.7859 0.3943 0.5825
1.0000 0.0252 0.1513 1.0000 0.6233 0.7754
1.0000 0.2562 0.0569 0.9553 1.0000 0.7295
0.1061 0.9988 0.2185 1.0000 0.9341 1.0000
现在,指定 "vector" 选项以便以向量形式返回输出。对于大型输入矩阵,以向量形式返回输出可以节省内存并提高效率。
[p,r,c] = equilibrate(A,"vector")p = 6×1
5
6
4
1
3
2
r = 6×1
0.1852
0.1749
0.1909
0.1588
0.1793
0.1966
c = 6×1
0.1799
0.1588
0.1588
0.2422
0.2066
0.2035
使用向量输出 p、r 和 c 构造经平衡处理的矩阵 Bvector。
Bvector = r.*A(p,:).*c'
Bvector = 6×6
1.0000 0.1471 1.0000 0.5385 0.5358 0.6031
0.1259 1.0000 0.8056 0.5509 0.6506 0.3916
0.2747 0.8485 1.0000 0.7859 0.3943 0.5825
1.0000 0.0252 0.1513 1.0000 0.6233 0.7754
1.0000 0.2562 0.0569 0.9553 1.0000 0.7295
0.1061 0.9988 0.2185 1.0000 0.9341 1.0000
比较 Bvector 和 Bmatrix。结果表明它们是相等的。
norm(Bmatrix - Bvector)
ans = 0
输入参数
输入矩阵,指定为方阵。A 可以是稠密矩阵,也可以是稀疏矩阵,但在结构上必须为非奇异矩阵,这由 sprank 决定。
当 A 为稀疏矩阵时,输出 P、R 和 C 也为稀疏矩阵。
数据类型: single | double
复数支持: 是
输出参量
置换信息,以矩阵或向量形式返回。P*A(或 A(P,:) 带 "vector" 选项)是 A 的置换,它使其对角线元素乘积的绝对值最大化。
行缩放,以对角矩阵或向量形式返回。R 和 C 中的非零项是正实数。
列缩放,以对角矩阵或向量形式返回。R 和 C 中的非零项是正实数。
详细信息
对于线性系统解 x = A\b,A 的条件数对于计算的准确度和效率很重要。equilibrate 可以通过重新缩放基向量来改进 A 的条件数。这实际上是形成一个新坐标系以便同时在其中表示 b 和 x。
当原始方程组 x = A\b 中的 b 和 x 向量的缩放不相关时,equilibrate 最有用。但是,如果 b 和 x 的缩放是相关的,则不推荐使用 equilibrate 来重新缩放 A 以仅用于线性系统求解。所获得的解通常不会产生原始方程组的小残差,即使使用原始基向量来表示也是如此。
参考
[1] Duff, I. S., and J. Koster. “On Algorithms For Permuting Large Entries to the Diagonal of a Sparse Matrix.” SIAM Journal on Matrix Analysis and Applications 22, no. 4 (January 2001): 973–96.
扩展功能
此函数完全支持基于线程的环境。有关详细信息,请参阅在基于线程的环境中运行 MATLAB 函数。
版本历史记录
在 R2019a 中推出将 outputForm 指定为 "vector" 或 "matrix",以控制 equilibrate 是以向量还是矩阵形式返回输出参量。对于大型分解,将输出作为向量返回可以节省内存并提高效率。
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)