gmres
求解线性系统 - 广义最小残差法
语法
说明
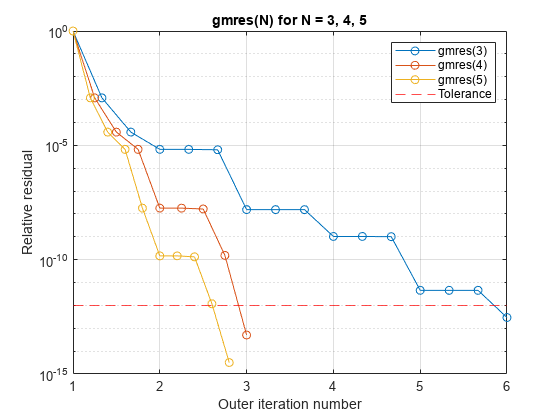
示例
输入参数
输出参量
详细信息
提示
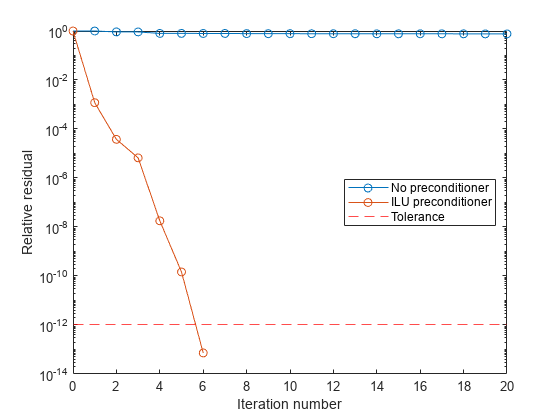
大多数迭代方法的收敛取决于系数矩阵的条件数
cond(A)。当A是方阵时,您可以使用equilibrate来改进其条件数,它本身就能使大多数迭代求解器更容易收敛。但如果您随后会对经平衡处理的矩阵B = R*P*A*C进行因式分解,使用equilibrate还可以获得质量更好的预条件子矩阵。您可以使用矩阵重新排序函数(如
dissect和symrcm)来置换系数矩阵的行和列,并在系数矩阵被分解以生成预条件子时最小化非零值的数量。这可以减少后续求解预条件线性系统所需的内存和时间。
参考
[1] Barrett, R., M. Berry, T. F. Chan, et al., Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, SIAM, Philadelphia, 1994.
[2] Saad, Yousef and Martin H. Schultz, “GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems,” SIAM J. Sci. Stat. Comput., July 1986, Vol. 7, No. 3, pp. 856-869.