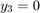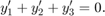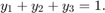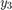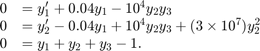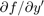ode15i

解算全隐式微分方程 - 变阶方法

全页折叠

语法

[t,y] = ode15i(odefun,tspan,y0,yp0)

[t,y] = ode15i(odefun,tspan,y0,yp0,options)

[t,y,te,ye,ie] = ode15i(odefun,tspan,y0,yp0,options)

sol = ode15i(___)

说明

示例

[t,y] = ode15i(odefun,tspan,y0,yp0)（其中 tspan = [t0 tf]）求微分方程组 $f (t, y, y') = 0$ 从 t0 到 tf 的积分，初始条件为 y0 和 yp0。解数组 y 中的每一行都与列向量 t 中返回的值相对应。

示例

[t,y] = ode15i(odefun,tspan,y0,yp0,options) 还使用由 options（使用 odeset 函数创建的参数）定义的积分设置。例如，使用 AbsTol 和 RelTol 选项指定绝对误差容限和相对误差容限，或者使用 Jacobian 选项提供雅可比矩阵。

[t,y,te,ye,ie] = ode15i(odefun,tspan,y0,yp0,options) 还求 (t,y,y') 的函数（称为事件函数）在何处为零。在输出中，te 是事件的时间，ye 是事件发生时的解，ie 是触发的事件的索引。

对于每个事件函数，应指定积分是否在零点处终止以及过零方向是否重要。为此，请将 'Events' 属性设置为函数（例如 myEventFcn 或 @myEventFcn），并创建一个对应的函数：[value,isterminal,direction] = myEventFcn(t,y,yp)。有关详细信息，请参阅 ODE 事件位置。

sol = ode15i(___) 返回一个结构体，您可以将该结构体与 deval 结合使用来计算区间 [t0 tf] 中任意点位置的解。您可以使用上述语法中的任何输入参数组合。

示例

全部折叠

求解 Weissinger 隐式 ODE

打开实时脚本

计算一致的初始条件，并用 ode15i 求解隐式 ODE。

Weissinger 方程是

${ty}^{2} {(y^{'})}^{3} - y^{3} {(y^{'})}^{2} + t (t^{2} + 1) y^{'} - t^{2} y = 0$ .

由于该方程采用一般形式 $f (t, y, y^{'}) = 0$ ，您可以使用 ode15i 函数来求解隐式微分方程。

编写方程代码

要以适合 ode15i 的形式对方程进行编码，您需要编写一个函数，该函数使用 $t$ 、 $y$ 和 $y^{'}$ 的输入并返回方程的残差值。可以使用函数 @weissinger 对此方程进行编码。查看函数文件。

type weissinger

function res = weissinger(t,y,yp)
%WEISSINGER  Evaluate the residual of the Weissinger implicit ODE
%
%   See also ODE15I.

%   Jacek Kierzenka and Lawrence F. Shampine
%   Copyright 1984-2014 The MathWorks, Inc.

res = t*y^2 * yp^3 - y^3 * yp^2 + t*(t^2 + 1)*yp - t^2 * y;

计算一致的初始条件

ode15i 求解器需要一致的初始条件，即提供给求解器的初始条件必须满足

$f (t_{0}, y, y^{'}) = 0$ .

由于可能会提供不一致的初始条件，并且 ode15i 不会检查一致性，因此建议您使用辅助函数 decic 来计算这些条件。decic 会固定一些指定的变量，并为不固定的变量计算一致的初始值。

在本例中，固定初始值 $y (t_{0}) = \sqrt{\frac{3}{2}}$ ，并让 decic 从 $y^{'} (t_{0}) = 0$ 的初始估计值开始，计算导数 $y^{'} (t_{0})$ 的一致初始值。

t0 = 1;
y0 = sqrt(3/2);
yp0 = 0;
[y0,yp0] = decic(@weissinger,t0,y0,1,yp0,0)

y0 = 1.2247

yp0 = 0.8165

求解方程

使用 decic 加上 ode15i 返回的一致初始条件，在时间区间 $[1 10]$ 上求解 ODE。

[t,y] = ode15i(@weissinger,[1 10],y0,yp0);

绘制结果

此 ODE 的精确解为

$y (t) = \sqrt{t^{2} + \frac{1}{2}}$ .

绘制 ode15i 计算的数值解 y 对解析解 ytrue 的图。

ytrue = sqrt(t.^2 + 0.5);
plot(t,y,'*',t,ytrue,'-o')
legend('ode15i', 'exact')

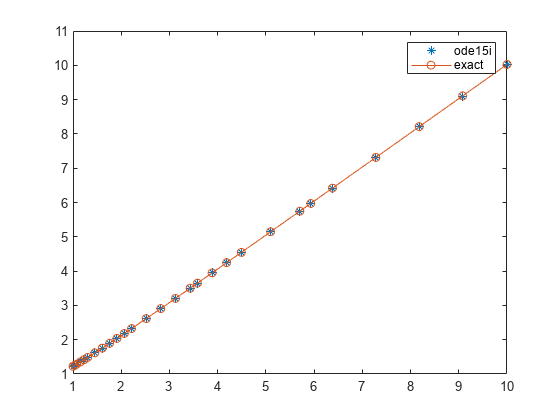
Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent ode15i, exact.

将 Robertson 问题作为隐式微分代数方程 (DAE) 求解

打开脚本

此示例将 ODE 方程组重新表示为完全隐式微分代数方程组 (DAE)。hb1ode.m 中编写的 Robertson 问题是解算刚性 ODE 的程序的经典测试问题。方程组为：

$\begin{array}{cl} y'_1 &= -0.04y_1 + 10^4 y_2y_3\\ y'_2 &= 0.04y_1 -
10^4 4y_2y_3-(3 \times 10^7)y_2^2\\ y'_3 &= (3 \times
10^7)y_2^2.\end{array}$

hb1ode 将此 ODE 方程组解算为稳定状态，初始条件为、和。但这些方程也满足线性守恒定律，

在解和初始条件方面，守恒定律为

通过使用守恒定律确定的状态，该问题可以重写为 DAE 方程组。问题可重新表示为隐式 DAE 方程组

$\begin{array}{cl} 0 &= y'_1 +0.04y_1 - 10^4 y_2y_3\\ 0 &= y'_2 -0.04y_1
+ 10^4 y_2y_3+(3 \times 10^7)y_2^2\\ 0 &= y_1 + y_2 + y_3 -
1.\end{array}$

函数 robertsidae 为此 DAE 方程组编码。

function res = robertsidae(t,y,yp)
res = [yp(1) + 0.04*y(1) - 1e4*y(2)*y(3);
   yp(2) - 0.04*y(1) + 1e4*y(2)*y(3) + 3e7*y(2)^2;
   y(1) + y(2) + y(3) - 1];

ihb1dae.m 中提供了用这种方法表示 Robertson 问题的完整示例代码。

设置误差容限和 $\partial f / \partial y'$ 的值。

options = odeset('RelTol',1e-4,'AbsTol',[1e-6 1e-10 1e-6], ...
   'Jacobian',{[],[1 0 0; 0 1 0; 0 0 0]});

使用 decic 根据估计值计算一致初始条件。固定 y0 的前两个分量以获得与在 hb1dae.m 中使用 ode15s 所求相同的一致初始条件。hb1dae.m 将此问题表示为半显式 DAE 方程组。

y0 = [1; 0; 1e-3];
yp0 = [0; 0; 0];
[y0,yp0] = decic(@robertsidae,0,y0,[1 1 0],yp0,[],options);

使用 ode15i 对 DAE 方程组求解。

tspan = [0 4*logspace(-6,6)];
[t,y] = ode15i(@robertsidae,tspan,y0,yp0,options);

绘制解分量。由于第二个解分量跟其他分量相比相对较小，所以绘制前将其乘以 1e4。

y(:,2) = 1e4*y(:,2);
semilogx(t,y)
ylabel('1e4 * y(:,2)')
title('Robertson DAE problem with a Conservation Law, solved by ODE15I')

输入参数

全部折叠

`odefun` — 要求解的函数
函数句柄

要求解的函数，指定为指向待积分器的句柄。

对于标量 t 以及列向量 y 和 yp 来说，函数 f = odefun(t,y,yp) 必须返回与 $f (t, y, y')$ 相对应的数据类型为 single 或 double 的列向量 f。odefun 必须接受 t、y 和 yp 这三个输入，即使其中某个输入未在函数中使用也是如此。

例如，要求解 $y' - y = 0$ ，请使用此函数。

function f = odefun(t,y,yp)
  f = yp - y;
end

对于方程组，odefun 的输出为向量。每个方程变成解向量中的一个元素。例如，要求解

$\begin{array}{l} y'_{1} - y_{2} = 0 \\ y'_{2} + 1 = 0, \end{array}$

，请使用以下函数。

function dy = odefun(t,y,yp)
  dy = zeros(2,1);
  dy(1) = yp(1)-y(2);
  dy(2) = yp(2)+1;
end

有关如何为函数 odefun 提供其他参数的信息，请参阅参数化函数。

示例： @myFcn

数据类型： function_handle

`tspan` — 积分区间
向量

积分区间，指定为向量。tspan 必须至少是一个二元素向量 [t0 tf]，用于指定初始时间和最终时间。要获取 t0 到 tf 之间的特定时间的解，请使用 [t0,t1,t2,...,tf] 形式的长向量。tspan 中的元素必须单调递增或单调递减。

求解器在初始时间 tspan(1) 施加由 y0 给出的初始条件，然后求 tspan(1) 到 tspan(end) 的积分：

如果 tspan 有两个元素，[t0 tf]，求解器将返回在该区间内的每个内部积分步计算的解。
如果 tspan 包含两个以上的元素，[t0,t1,t2,...,tf]，求解器将返回在给定点处计算的解。但是，求解器不会精确步进到 tspan 中指定的每个点。此时，求解器使用自己的内部积分步来计算解，然后在 tspan 中请求的各点处计算解。在指定点处生成的解与在每个内部积分步计算的解具有相同的准确度级别。
指定多个中间点对计算效率影响甚微，但在大型系统中可能会影响内存管理。

求解器使用 tspan 的值计算 InitialStep 和 MaxStep 的合适值：

如果 tspan 包含多个中间点 [t0,t1,t2,...,tf]，则指定的点表示了问题的规模，这可能影响求解器使用的 InitialStep 的值。因此，根据您是将 tspan 指定为二元素向量还是包含中间点的向量，求解器获得的解可能有所不同。
tspan 中的初始值和最终值用于计算最大步长 MaxStep。因此，更改 tspan 中的初始值或最终值可能导致求解器使用不同步长序列，从而可能会更改解。

示例： [1 10]

示例： [1 3 5 7 9 10]

数据类型： single | double

`y0` — y 的初始条件
向量

y 的初始条件，指定为向量。y0 的长度必须与 odefun 的向量输出相同，使 y0 包含与 odefun 中定义的每个方程对应的一个初始条件。

y0 和 yp0 的初始条件必须保持一致，也就是说 $f (t_{0}, y_{0}, y'_{0}) = 0$ 。使用 decic 函数计算接近猜想值的一致初始条件。

数据类型： single | double

`yp0` — y’ 的初始条件
列向量

y’ 的初始条件，指定为列向量。yp0 的长度必须与 odefun 的向量输出相同，使 yp0 包含与 odefun 中定义的每个变量对应的一个初始条件。

y0 和 yp0 的初始条件必须保持一致，也就是说 $f (t_{0}, y_{0}, y'_{0}) = 0$ 。使用 decic 函数计算接近猜想值的一致初始条件。

数据类型： single | double

`options` — options 结构体
结构体数组

options 结构体，指定为结构体数组。可以使用 odeset 函数创建或修改 options 结构体。

有关与每个 ODE 求解器兼容的选项列表，请参阅 ODE 选项摘要。

示例： options = odeset('RelTol',1e-5,'Stats','on','OutputFcn',@odeplot) 指定 1e-5 的相对误差容限、打开求解器统计信息的显示，并指定输出函数 @odeplot 在计算时绘制解。

数据类型： struct

输出参数

全部折叠

`t` — 求值点
列向量

计算点，以列向量形式返回。

如果 tspan 包含两个元素 [t0 tf]，则 t 包含用于执行积分的内部计算点。
如果 tspan 包含两个以上元素，则 t 与 tspan 相同。

`y` — 解
数组

解，以数组形式返回。y 中的每一行都与 t 的相应行中返回的值处的解相对应。

`te` — 事件的时间
列向量

事件的时间，以列向量形式返回。te 中的事件时间对应于 ye 中返回的解，而 ie 指定发生了哪个事件。

`ye` — 事件时间处的解
数组

事件时间的解，以数组形式返回。te 中的事件时间对应于 ye 中返回的解，而 ie 指定发生了哪个事件。

`ie` — 触发的事件函数的索引
列向量

触发的事件函数的索引，以列向量形式返回。te 中的事件时间对应于 ye 中返回的解，而 ie 指定发生了哪个事件。

`sol` — 用于计算的结构体
结构体数组

用于计算的结构体，以结构体数组形式返回。此结构体与 deval 函数一起使用，用于计算区间 [t0 tf] 内任何点的解。sol 结构体数组始终包括下列字段：

结构体字段	描述
`sol.x`	求解器选择的步的行向量。
`sol.y`	解。每列 `sol.y(:,i)` 包含时间 `sol.x(i)` 处的解。
`sol.solver`	求解器名称。

此外，如果指定了 odeset 的 Events 选项并且检测到事件，则 sol 还包括下列字段：

结构体字段	描述
`sol.xe`	事件发生的点。`sol.xe(end)` 包含终止事件（如果有）的确切点。
`sol.ye`	与 `sol.xe` 中的事件相对应的解。
`sol.ie`	`Events` 选项中指定的函数所返回的向量的索引。这些值指示求解器检测到的事件。

提示

为 ode15i 提供雅可比矩阵对可靠性和效率至关重要。对于大型稀疏方程组，提供雅可比稀疏模式也有助于求解器进行计算。在任一情况下，都要使用 odeset，采用 Jacobian 或 JPattern 选项将矩阵传入。

算法

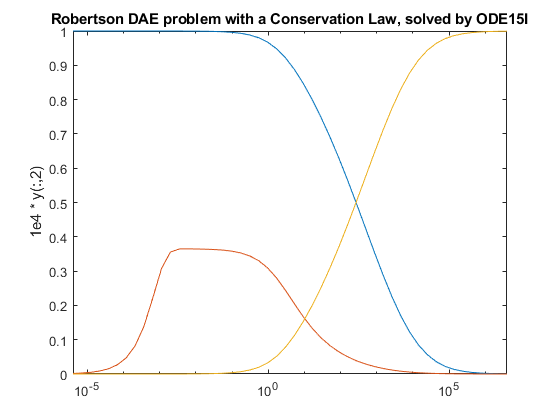
ode15i 是基于 1 到 5 阶后向差分公式 (BDF) 的变步长、可变阶数 (VSVO) 求解器。ode15i 用于完全隐式微分方程和指数为 1 的微分代数方程 (DAE)。辅助函数 decic 计算适合与 ode15i [1] 一起使用的一致初始条件。

参考

[1] Lawrence F. Shampine, “Solving 0 = F(t, y(t), y′(t)) in MATLAB,” Journal of Numerical Mathematics, Vol.10, No.4, 2002, pp. 291-310.

版本历史记录

在 R2006a 之前推出

另请参阅

ode15i

语法

说明

示例

求解 Weissinger 隐式 ODE

将 Robertson 问题作为隐式微分代数方程 (DAE) 求解

输入参数

odefun — 要求解的函数 函数句柄

tspan — 积分区间 向量

y0 — y 的初始条件 向量

yp0 — y’ 的初始条件 列向量

options — options 结构体 结构体数组

输出参数

t — 求值点 列向量

y — 解 数组

te — 事件的时间 列向量

ye — 事件时间处的解 数组

ie — 触发的事件函数的索引 列向量

sol — 用于计算的结构体 结构体数组

提示

算法

参考

版本历史记录

另请参阅

主题

WeChat

`odefun` — 要求解的函数
函数句柄

`tspan` — 积分区间
向量

`y0` — y 的初始条件
向量

`yp0` — y’ 的初始条件
列向量

`options` — options 结构体
结构体数组

`t` — 求值点
列向量

`y` — 解
数组

`te` — 事件的时间
列向量

`ye` — 事件时间处的解
数组

`ie` — 触发的事件函数的索引
列向量

`sol` — 用于计算的结构体
结构体数组